人教版七年级上数学教学4.3.3 余角和补角课件(共23张PPT)
文档属性
| 名称 | 人教版七年级上数学教学4.3.3 余角和补角课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 16:01:52 | ||
图片预览



文档简介
(共23张PPT)
4.3.3
余角和补角
1.在具体的现实情境中,认识一个角的余角与补角,掌握余角和补角的性质.
2.了解方位角,能确定具体物体的方位.
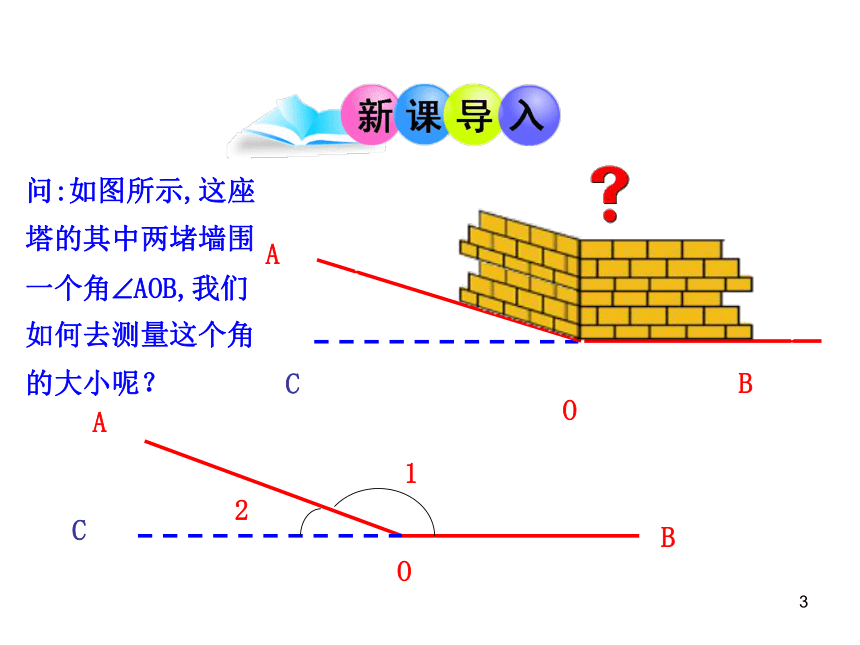
问:如图所示,这座塔的其中两堵墙围一个角?AOB,我们如何去测量这个角的大小呢?
C
B
A
O
A
C
O
B
1
2
1
2
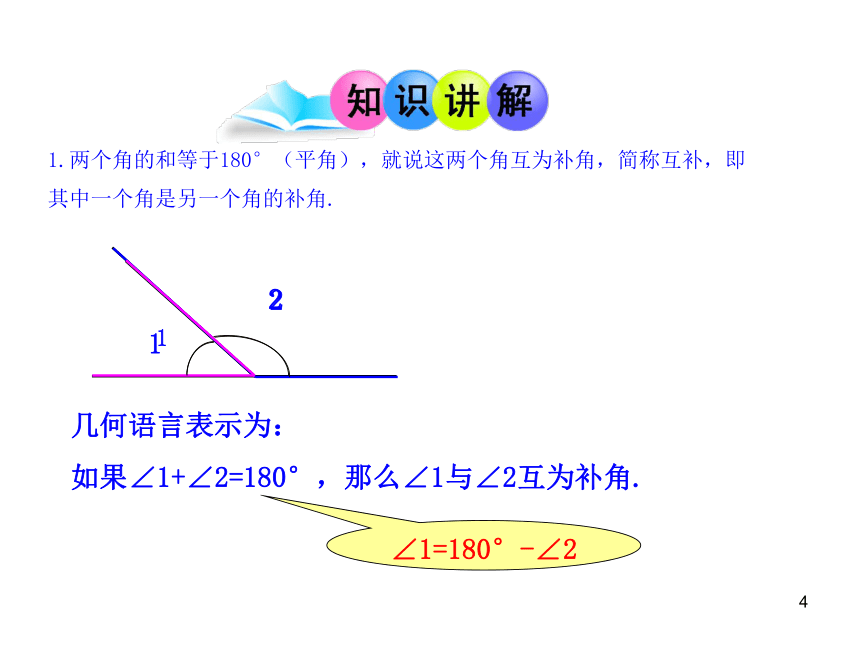
1.两个角的和等于180°(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个角的补角.
几何语言表示为:
如果∠1+∠2=180°,那么∠1与∠2互为补角.
2
1
∠1=180°-∠2
如图∠AOD
=
90°
∠1+∠2
=
90°
0
A
D
2.两个角的和等于90°(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角.
1
2
几何语言表示为:
如果∠1+∠2=90°,那么∠1与∠2互为余角.
∠1=90°
—∠2
1
2
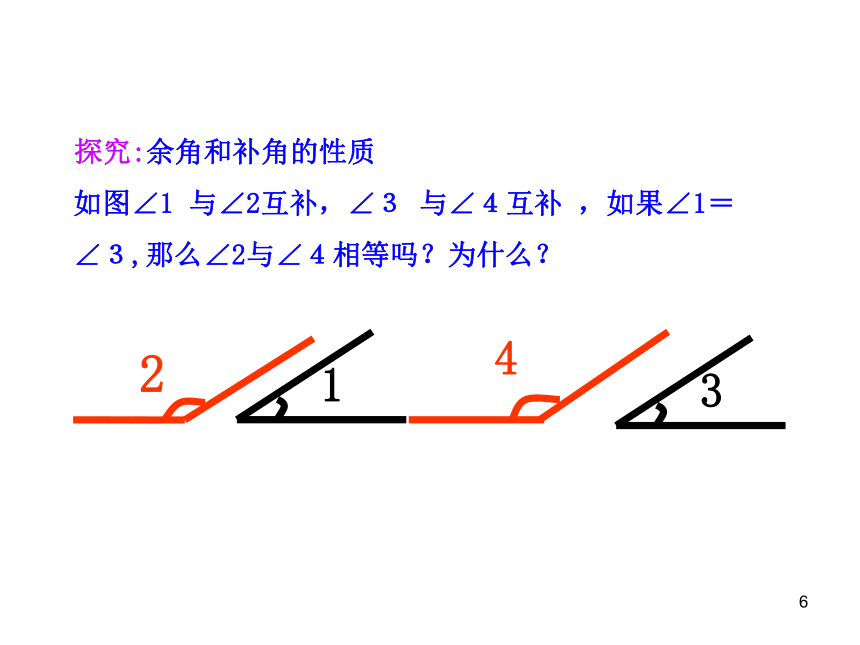
如图∠1
与∠2互补,∠3
与∠4互补
,如果∠1=
∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
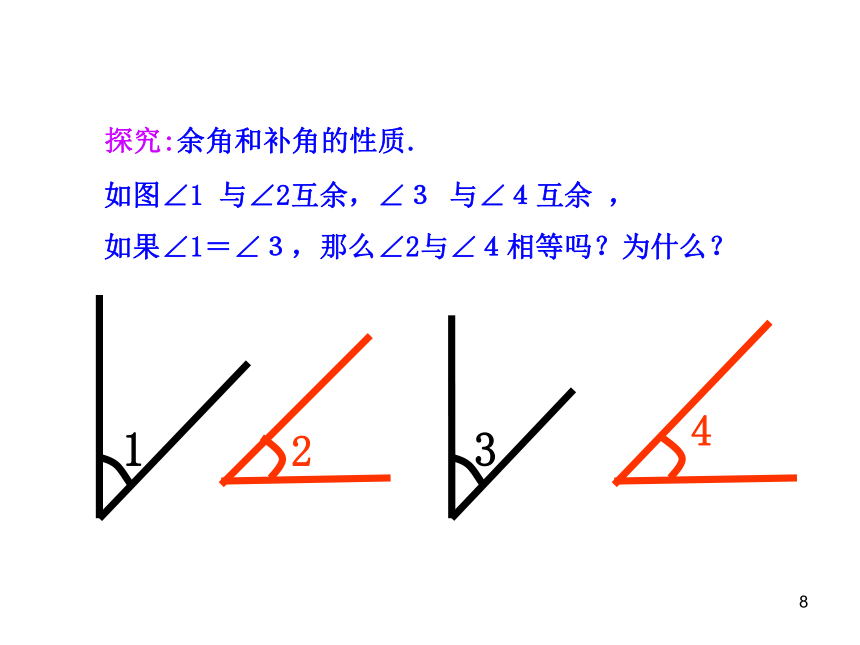
探究:余角和补角的性质
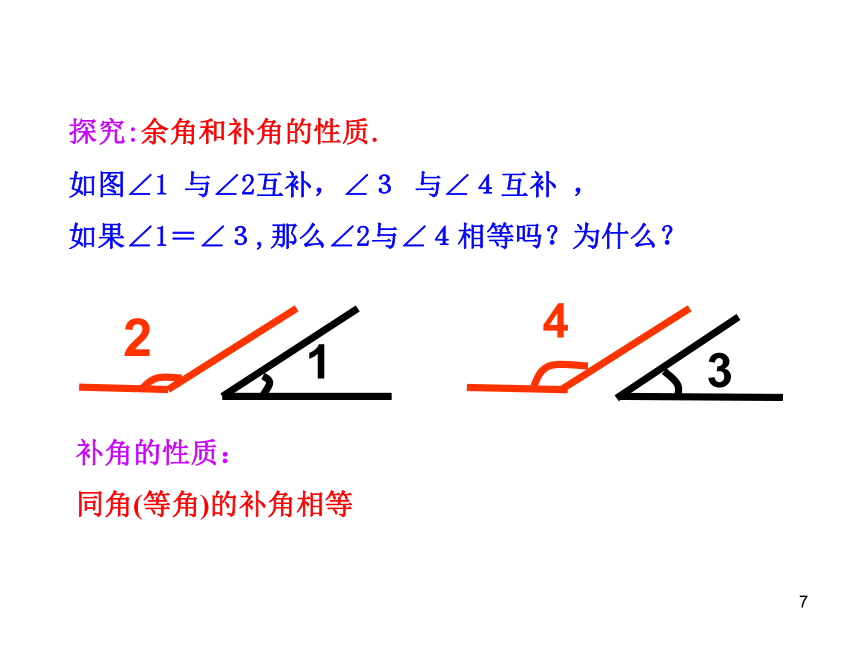
如图∠1
与∠2互补,∠3
与∠4互补
,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究:余角和补角的性质.
补角的性质:
同角(等角)的补角相等
如图∠1
与∠2互余,∠3
与∠4互余
,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
探究:余角和补角的性质.
1
2
4
3
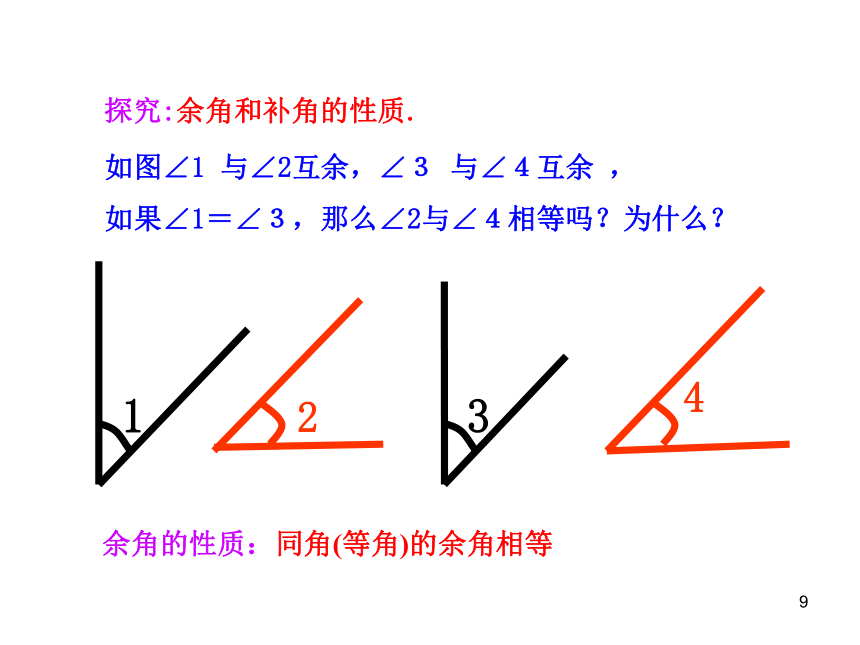
如图∠1
与∠2互余,∠3
与∠4互余
,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
探究:余角和补角的性质.
1
2
4
3
余角的性质:同角(等角)的余角相等
填空:我来试一试,我能行.
∠α
∠α的余角
∠α的补角
5°
45°
62°23′
x°
27°37′
117°37′
90°
-
5°
175°
45°
135°
(
180-x)°
85
°
180
°-
5
°
(角x为锐角)
(
90-x)°
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA,
A
B
C
D
OB,
OC,
OD,
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
O
北
南
西
东
(3)南偏西25°:
25°
北偏西70°:
南偏东60°:
A
B
C
射线OA
射线OB
射线OC
70°
60°
甲地
乙地
甲地对乙地的方位角
1.
先找出中心点,然后画出方向指标;
甲地
乙地
甲地对乙地的方位角
2.
把中心点和目的地用线连接起来;
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和蓝色线之间的角度.
北
东
西
北
南
●
A
说出B在A的
B
●
40°
那么A在B的
北偏东40°,
南偏西40°.
如图所示,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
●
A
60°
●
B
●
D
射线OB的方向就是北偏东40°,即客轮B所在的方向.
C
●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是北偏西45°,即海岛D所在的方向.
45°
1.图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
2.识图填空:
如图所示,O是直线AB上的一点,
OC是∠AOB的平分线.
(1)∠AOD的补角是_______.
(2)∠AOD的余角是_________.
A
O
B
D
C
∠BOD
∠COD
(1)钝角没有余角,但一定有补角.(
)
(2)一个锐角的余角一定比这个角大.(
)
(3)若两个角互补,则一个为锐角,一个为钝角.
(
)
(4)若一个角的余角是45°12′,则这个角的补角是135°12′.(
)
错误
正确
错误
正确
3.判断正误:
4.(临沂中考)如果
,那么
的余角的度数是(
).
(A)30°
(B)60°
(C)90°
(D)120°
【解析】选A.
90°-
60°=30°.
5.(佛山中考)30°角的补角是(
).
A.30°角
B.
60°角
C.
90°角
D.
150°角
【解析】选D.180°-30°=
150°.
6.一个角的补角是它的3倍,这个角是多少度?
解:设这个角为x°,
则这个角的补角是(180-x)°.
由题意得180-x=3x,
解得:
x
=
45,
则这个角的度数为45°.
变式训练:已知一个角的补角是这个角的余角的4倍,求这个角的度数.
设这个角为x°.由题意得180-x=4(90-x),解得:x=60.
通过本节课的学习,要求学生:
1.
认识一个角的余角与补角,掌握余角和补角的性质.
2.了解方位角,能确定具体物体的方位.
4.3.3
余角和补角
1.在具体的现实情境中,认识一个角的余角与补角,掌握余角和补角的性质.
2.了解方位角,能确定具体物体的方位.
问:如图所示,这座塔的其中两堵墙围一个角?AOB,我们如何去测量这个角的大小呢?
C
B
A
O
A
C
O
B
1
2
1
2
1.两个角的和等于180°(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个角的补角.
几何语言表示为:
如果∠1+∠2=180°,那么∠1与∠2互为补角.
2
1
∠1=180°-∠2
如图∠AOD
=
90°
∠1+∠2
=
90°
0
A
D
2.两个角的和等于90°(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角.
1
2
几何语言表示为:
如果∠1+∠2=90°,那么∠1与∠2互为余角.
∠1=90°
—∠2
1
2
如图∠1
与∠2互补,∠3
与∠4互补
,如果∠1=
∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究:余角和补角的性质
如图∠1
与∠2互补,∠3
与∠4互补
,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究:余角和补角的性质.
补角的性质:
同角(等角)的补角相等
如图∠1
与∠2互余,∠3
与∠4互余
,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
探究:余角和补角的性质.
1
2
4
3
如图∠1
与∠2互余,∠3
与∠4互余
,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
探究:余角和补角的性质.
1
2
4
3
余角的性质:同角(等角)的余角相等
填空:我来试一试,我能行.
∠α
∠α的余角
∠α的补角
5°
45°
62°23′
x°
27°37′
117°37′
90°
-
5°
175°
45°
135°
(
180-x)°
85
°
180
°-
5
°
(角x为锐角)
(
90-x)°
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA,
A
B
C
D
OB,
OC,
OD,
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
O
北
南
西
东
(3)南偏西25°:
25°
北偏西70°:
南偏东60°:
A
B
C
射线OA
射线OB
射线OC
70°
60°
甲地
乙地
甲地对乙地的方位角
1.
先找出中心点,然后画出方向指标;
甲地
乙地
甲地对乙地的方位角
2.
把中心点和目的地用线连接起来;
甲地
乙地
乙地对甲地的方位角
3.度量向北的射线和蓝色线之间的角度.
北
东
西
北
南
●
A
说出B在A的
B
●
40°
那么A在B的
北偏东40°,
南偏西40°.
如图所示,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
●
A
60°
●
B
●
D
射线OB的方向就是北偏东40°,即客轮B所在的方向.
C
●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向.
射线OD的方向就是北偏西45°,即海岛D所在的方向.
45°
1.图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
2.识图填空:
如图所示,O是直线AB上的一点,
OC是∠AOB的平分线.
(1)∠AOD的补角是_______.
(2)∠AOD的余角是_________.
A
O
B
D
C
∠BOD
∠COD
(1)钝角没有余角,但一定有补角.(
)
(2)一个锐角的余角一定比这个角大.(
)
(3)若两个角互补,则一个为锐角,一个为钝角.
(
)
(4)若一个角的余角是45°12′,则这个角的补角是135°12′.(
)
错误
正确
错误
正确
3.判断正误:
4.(临沂中考)如果
,那么
的余角的度数是(
).
(A)30°
(B)60°
(C)90°
(D)120°
【解析】选A.
90°-
60°=30°.
5.(佛山中考)30°角的补角是(
).
A.30°角
B.
60°角
C.
90°角
D.
150°角
【解析】选D.180°-30°=
150°.
6.一个角的补角是它的3倍,这个角是多少度?
解:设这个角为x°,
则这个角的补角是(180-x)°.
由题意得180-x=3x,
解得:
x
=
45,
则这个角的度数为45°.
变式训练:已知一个角的补角是这个角的余角的4倍,求这个角的度数.
设这个角为x°.由题意得180-x=4(90-x),解得:x=60.
通过本节课的学习,要求学生:
1.
认识一个角的余角与补角,掌握余角和补角的性质.
2.了解方位角,能确定具体物体的方位.
