全等三角形
图片预览


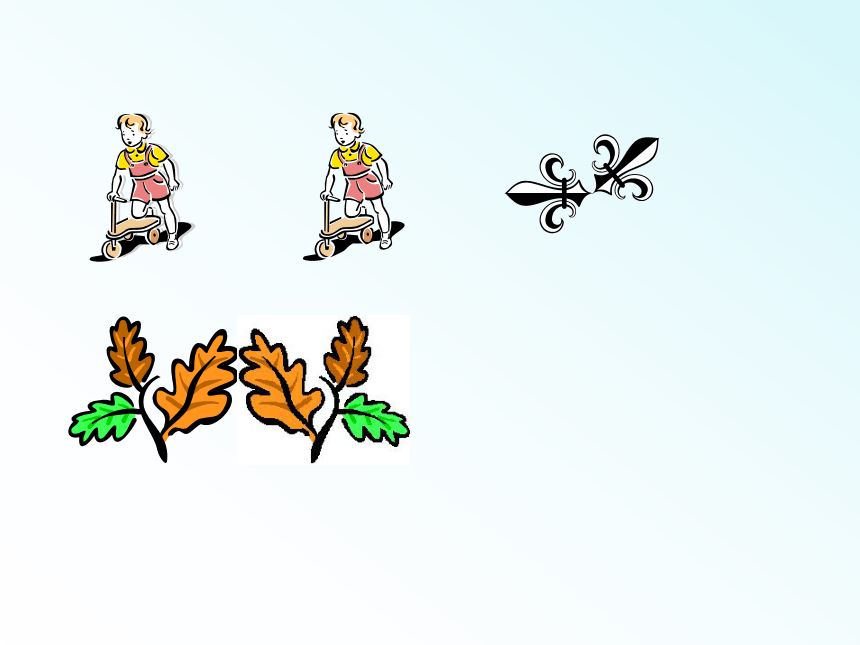



文档简介
(共27张PPT)
11.1 全等三角形
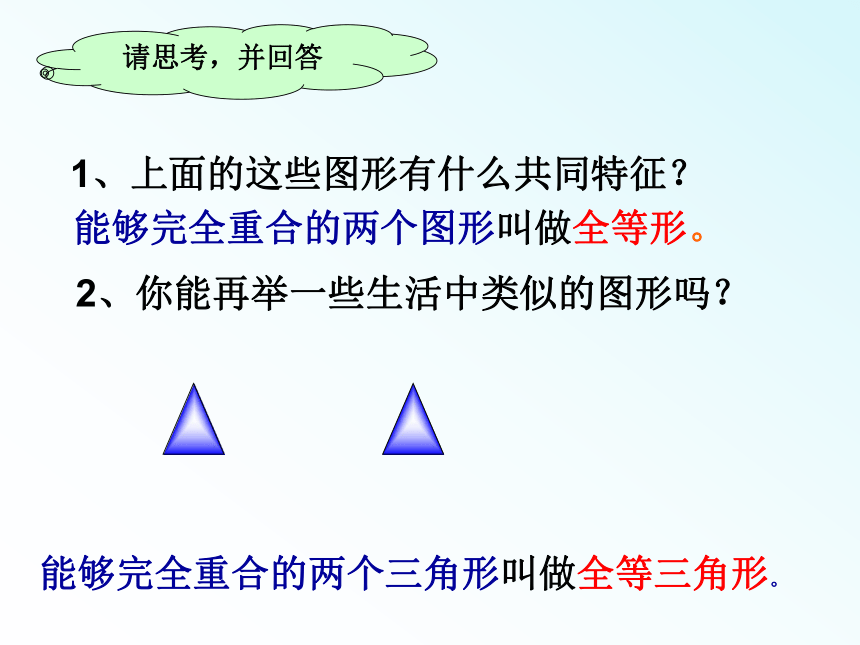
请思考,并回答
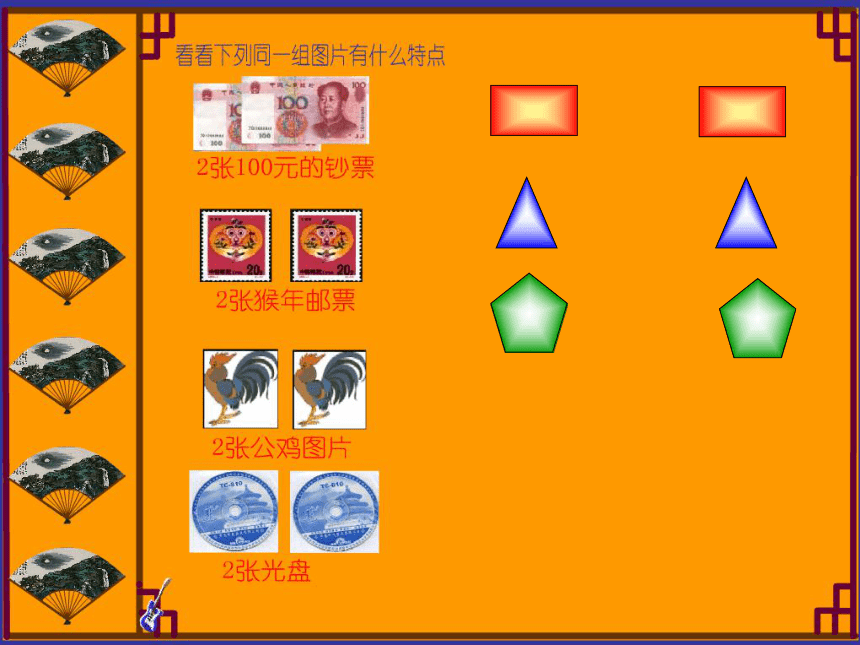
1、上面的这些图形有什么共同特征?
2、你能再举一些生活中类似的图形吗?
能够完全重合的两个图形叫做全等形。
能够完全重合的两个三角形叫做全等三角形。
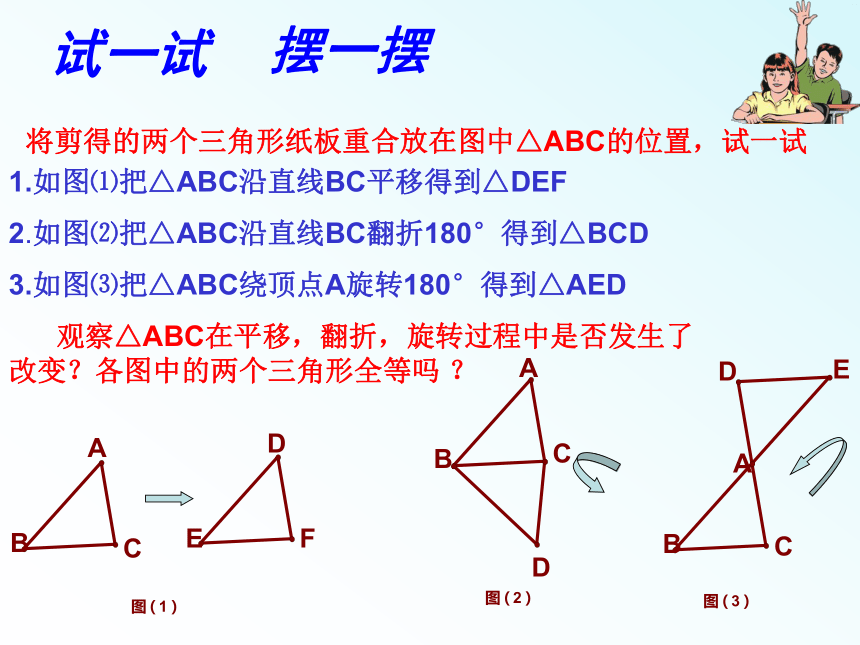
试一试
1.如图⑴把△ABC沿直线BC平移得到△DEF
2.如图⑵把△ABC沿直线BC翻折180°得到△BCD
3.如图⑶把△ABC绕顶点A旋转180°得到△AED
观察△ABC在平移,翻折,旋转过程中是否发生了改变?各图中的两个三角形全等吗 ?
将剪得的两个三角形纸板重合放在图中△ABC的位置,试一试
摆一摆
结论:一个图形经过平移、翻折、旋转后,位置变化了,
但___和___都没有改变,即平移、翻折、旋转前后的
图形__。
形状
大小
全等
A
B
C
E
D
F
1、能够完全重合的两个三角形,叫做
全等三角形.
(一)全等三角形的概念
E
D
F
2、把两个三角形重合到一起.重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应顶点是点A和点D,点B和点E,点C和点F;
A
B
C
(一)全等三角形的概念
E
D
F
2、把两个三角形重合到一起.重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应边是AB和DE,AC和DE,BC和EF;
对应角是∠A和∠D,∠B和∠E ,∠C和∠F.
A
B
C
E
D
F
(一)全等三角形的概念
“全等”用符号“≌ ”表示
3、全等三角形的表示法
图中的△ABC和△DEF全等,
记作:△ABC≌ △DEF
读作:△ABC全等于△DEF
注意
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
你能否直接从记作 ABC≌ DEF中判断出所有的对应顶点、对应边和对应角?
A
B
C
D
E
F
想一想
这样表示好吗?
△ABC≌ △DEF
A
B
C
E
D
F
(二)全等三角形的性质
全等三角形的对应边相等;
全等三角形的对应角相等.
E
D
F
∵△ABC≌ △DEF
(已知)
∴ AB=DE,AC=DF,BC=EF
(全等三角形的对应边相等)
∠A=∠D,∠B=∠E ,∠C=∠F
(全等三角形的对应角相等)
小结
1、能够完全重合的两个三角形叫做全等三角形。
2、两个全等三角形重合到一起,重合的顶点叫做
对应顶点,重合的边叫做对应边,重合的角叫做对应角。
3、“全等”用符号“≌ ”表示。
4、全等三角形的性质:全等三角形的对应边相等;
全等三角形的对应角相等。
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共顶点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,
对应边所对的角是对应角.
5.在两个全等三角形中
最长边对最长边,
最短边对最短边,
最大角对最大角,
最小角对最小角。
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,对应边所对的角是对应角.
5.在两个全等三角形中最长边对最长边,最短边对最短边,最大角对最大角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACD,BD= ,
∠BDA=
A
B
C
D
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
(四)
1、请填空
BD
∠B
CD
∠CDA
CD
∠DCA
2、请选择
(1) △ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=5cm,BD=4cm,AD=6cm,那么BC的长是( )
(A)6cm (B)5cm (C)4cm ( D)无法确定
(2)在上题中, ∠CAB的对应角是( )
(A)∠DAB (B) ∠ DBA
(C) ∠ DBC (D) ∠ CAD
(四)
A
B
A
C
D
B
(四)
3、写一写
如图,△ABN≌ △ACM,∠B和∠C是对应角,AB与AC是对应边,写出其它的对应边及对应角。
M
A
B
N
C
解:其它的对应边是AM和AN,BN和CM;其它的对应角是∠ANB和∠AMC,∠BAN和∠CAM。
1.本节课我们学习了哪些内容
2.全等三角形有那些性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
全等形,全等三角形的概念;
全等三角形的有些性质;
找全等三角形的对应边,对应角的规律.
1.如图,已知△ AOC ≌ △BOD
求证:AC∥BD
2、如图
△ABD≌ △EBC,AB=3cm,BC=5cm,
求DE的长.
教材第4页
习题11.1第2、3题写在A本上
11.1 全等三角形
请思考,并回答
1、上面的这些图形有什么共同特征?
2、你能再举一些生活中类似的图形吗?
能够完全重合的两个图形叫做全等形。
能够完全重合的两个三角形叫做全等三角形。
试一试
1.如图⑴把△ABC沿直线BC平移得到△DEF
2.如图⑵把△ABC沿直线BC翻折180°得到△BCD
3.如图⑶把△ABC绕顶点A旋转180°得到△AED
观察△ABC在平移,翻折,旋转过程中是否发生了改变?各图中的两个三角形全等吗 ?
将剪得的两个三角形纸板重合放在图中△ABC的位置,试一试
摆一摆
结论:一个图形经过平移、翻折、旋转后,位置变化了,
但___和___都没有改变,即平移、翻折、旋转前后的
图形__。
形状
大小
全等
A
B
C
E
D
F
1、能够完全重合的两个三角形,叫做
全等三角形.
(一)全等三角形的概念
E
D
F
2、把两个三角形重合到一起.重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应顶点是点A和点D,点B和点E,点C和点F;
A
B
C
(一)全等三角形的概念
E
D
F
2、把两个三角形重合到一起.重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
对应边是AB和DE,AC和DE,BC和EF;
对应角是∠A和∠D,∠B和∠E ,∠C和∠F.
A
B
C
E
D
F
(一)全等三角形的概念
“全等”用符号“≌ ”表示
3、全等三角形的表示法
图中的△ABC和△DEF全等,
记作:△ABC≌ △DEF
读作:△ABC全等于△DEF
注意
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
你能否直接从记作 ABC≌ DEF中判断出所有的对应顶点、对应边和对应角?
A
B
C
D
E
F
想一想
这样表示好吗?
△ABC≌ △DEF
A
B
C
E
D
F
(二)全等三角形的性质
全等三角形的对应边相等;
全等三角形的对应角相等.
E
D
F
∵△ABC≌ △DEF
(已知)
∴ AB=DE,AC=DF,BC=EF
(全等三角形的对应边相等)
∠A=∠D,∠B=∠E ,∠C=∠F
(全等三角形的对应角相等)
小结
1、能够完全重合的两个三角形叫做全等三角形。
2、两个全等三角形重合到一起,重合的顶点叫做
对应顶点,重合的边叫做对应边,重合的角叫做对应角。
3、“全等”用符号“≌ ”表示。
4、全等三角形的性质:全等三角形的对应边相等;
全等三角形的对应角相等。
1、有公共边
A
B
C
D
A
B
C
D
A
B
C
D
2、有公共顶点
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,
对应边所对的角是对应角.
5.在两个全等三角形中
最长边对最长边,
最短边对最短边,
最大角对最大角,
最小角对最小角。
3.有公共角的,公共角一定是对应角。
4.对应角所对的边是对应边,对应边所对的角是对应角.
5.在两个全等三角形中最长边对最长边,最短边对最短边,最大角对最大角,最小角对最小角。
1.有公共边的,公共边一定是对应边。
2.有对顶角的,对顶角一定是对应角。
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACD,BD= ,
∠BDA=
A
B
C
D
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
(四)
1、请填空
BD
∠B
CD
∠CDA
CD
∠DCA
2、请选择
(1) △ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=5cm,BD=4cm,AD=6cm,那么BC的长是( )
(A)6cm (B)5cm (C)4cm ( D)无法确定
(2)在上题中, ∠CAB的对应角是( )
(A)∠DAB (B) ∠ DBA
(C) ∠ DBC (D) ∠ CAD
(四)
A
B
A
C
D
B
(四)
3、写一写
如图,△ABN≌ △ACM,∠B和∠C是对应角,AB与AC是对应边,写出其它的对应边及对应角。
M
A
B
N
C
解:其它的对应边是AM和AN,BN和CM;其它的对应角是∠ANB和∠AMC,∠BAN和∠CAM。
1.本节课我们学习了哪些内容
2.全等三角形有那些性质
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
全等形,全等三角形的概念;
全等三角形的有些性质;
找全等三角形的对应边,对应角的规律.
1.如图,已知△ AOC ≌ △BOD
求证:AC∥BD
2、如图
△ABD≌ △EBC,AB=3cm,BC=5cm,
求DE的长.
教材第4页
习题11.1第2、3题写在A本上
