2020-2021学年山东省济宁市任城区六年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省济宁市任城区六年级(下)期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 684.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览


文档简介
2020-2021学年山东省济宁市任城区六年级(下)期末数学试卷(五四学制)
一.选择题(共10小题,每题3分,共30分).
1.下列调查中,适合用抽样调查的是( )
A.返校前每个班级学生健康码情况调查
B.对乘坐高铁的乘客进行安检
C.调查一批防疫口罩的质量情况
D.对新研发导弹的零部件进行检查
2.世界最大的单口径球面射电望远镜被誉为“中国天眼”,在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒.数据0.00519用科学记数法可以表示为( )
A.5.19×10﹣3 B.5.19×10﹣4 C.5.19×10﹣5 D.5.19×10﹣6
3.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列正确的语句是( )
A.线段PC的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段AC的长是点C到直线PA的距离
4.下列运算正确的是( )
A.2x2y+3xy=5x3y2 B.(﹣2ab2)3=﹣6a3b6
C.(3a+b)2=9a2+b2 D.(3a+b)(3a﹣b)=9a2﹣b2
5.如图,已知AB=10cm,点C在线段AB上,且AC=6cm,点E是线段AC的中点,点D是线段BC的中点.则DE的长为( )
A.4cm B.5cm C.6cm D.7cm
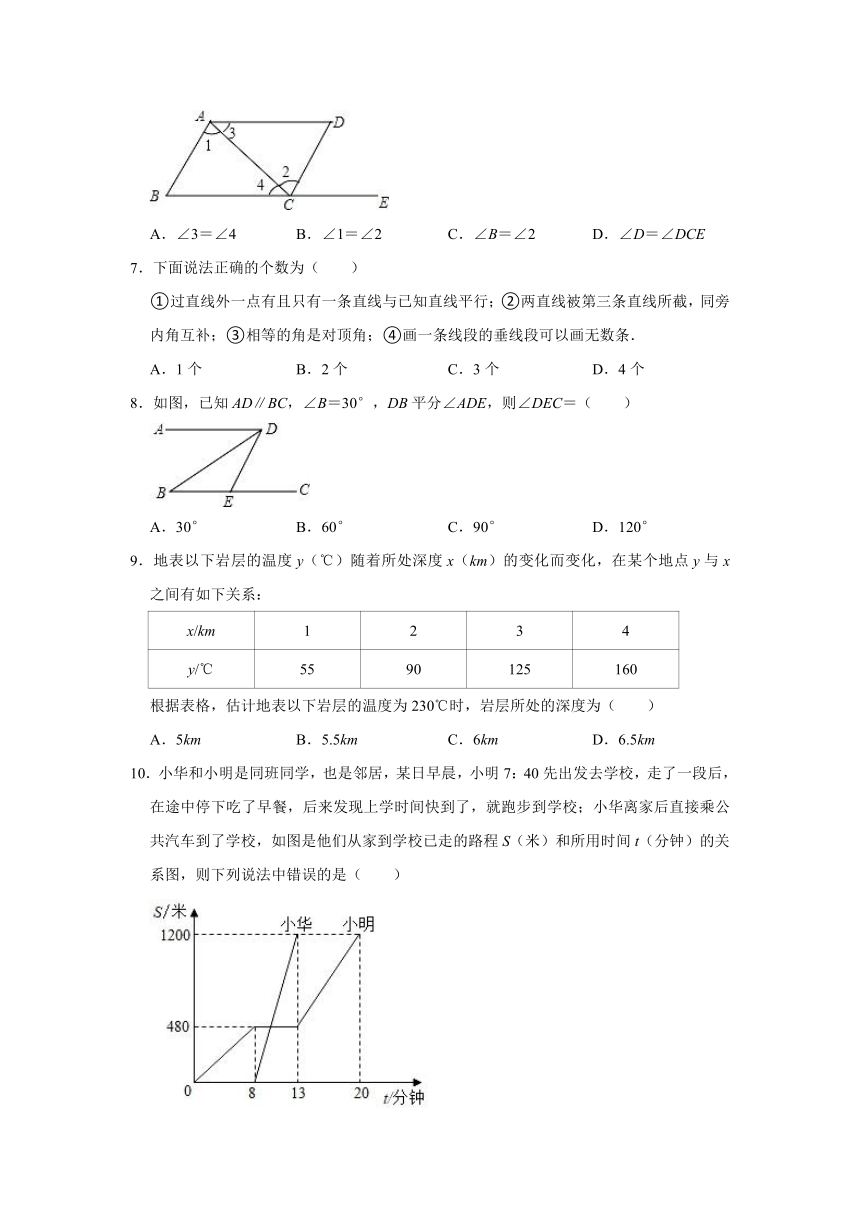
6.如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2 C.∠B=∠2 D.∠D=∠DCE
7.下面说法正确的个数为( )
①过直线外一点有且只有一条直线与已知直线平行;②两直线被第三条直线所截,同旁内角互补;③相等的角是对顶角;④画一条线段的垂线段可以画无数条.
A.1个 B.2个 C.3个 D.4个
8.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=( )
A.30° B.60° C.90° D.120°
9.地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km 1 2 3 4
y/℃ 55 90 125 160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为( )
A.5km B.5.5km C.6km D.6.5km
10.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
二.填空题(每小题3分,共15分)
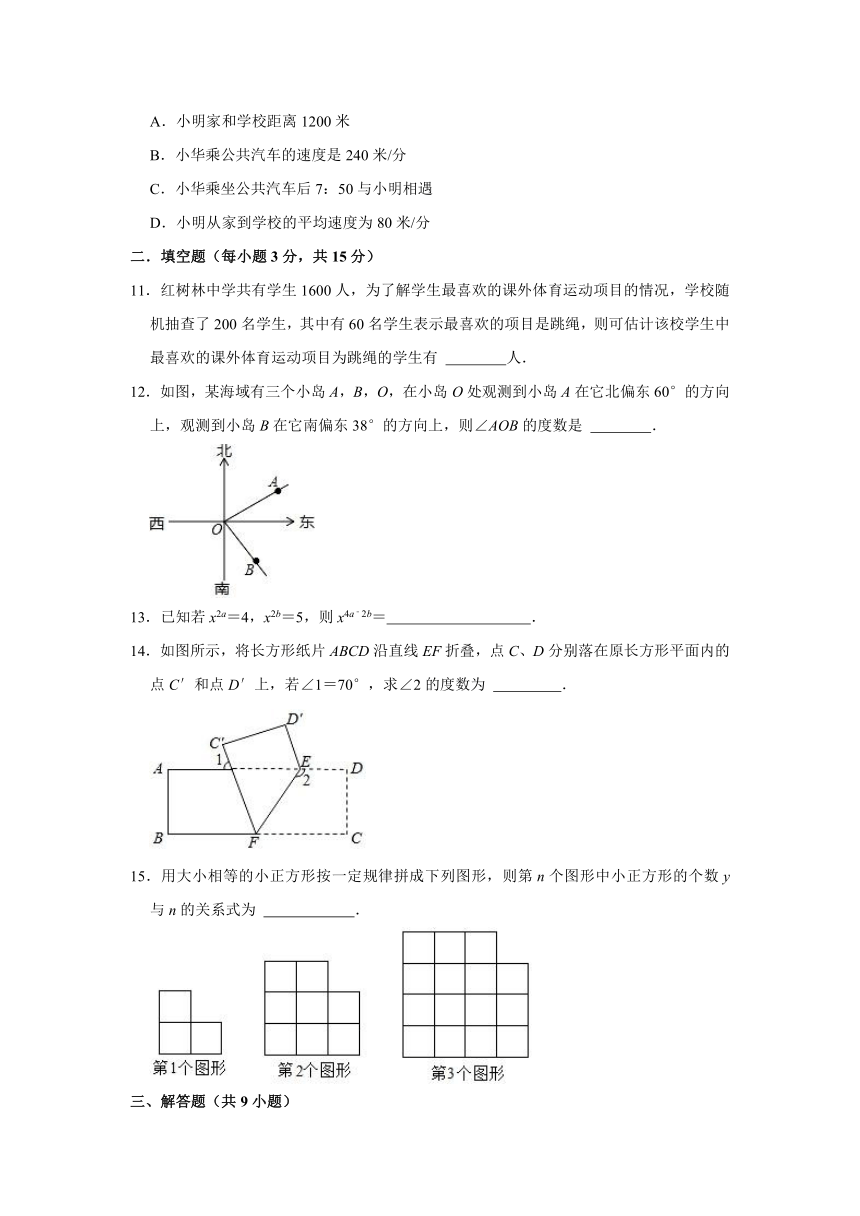
11.红树林中学共有学生1600人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了200名学生,其中有60名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有 人.
12.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是 .
13.已知若x2a=4,x2b=5,则x4a﹣2b= .
14.如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在原长方形平面内的点C′和点D′上,若∠1=70°,求∠2的度数为 .
15.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数y与n的关系式为 .
三、解答题(共9小题)
16.计算.
(1)(3x2y3﹣x3y4)÷(2x2y2).
(2)(a+3b)(2a﹣b).
17.先化简,再求值:2x2﹣(2x+3y)(2x﹣3y)﹣(x﹣3y)2,其中x=2,y=.
18.如图,已知∠MAN,点B在射线AM上,尺规作图:
(1)在AN上取一点C,使AC=BA;
(2)作∠MBD=∠MAN.(保留作图痕迹,不写作法)
19.某学校为了解共青团员志愿服务情况,调查小组根据平台数据进行了抽样问卷调查,过程如下:
(1)从九年级随机抽取40名共青团员,将其志愿服务时间按如下方式分组:A:0~5小时;B:5~10小时;C:10~15小时;D:15~20小时;E:20~25小时;F:25~30小时.(注:每组含最小值,不含最大值)得到这40名志愿者服务时间如下:BDEACEDBFCDDDBECDEEFAFFADCDBDFCFDECEEECE
并将上述数据整理在频数分布表中,请你补充其中的数据.
志愿服务时间 A B C D E F
频数 3 4 10 9 7
(2)根据上面的频数分布表,小明绘制了频数分布直方图,请将空缺的部分补充完整;
(3)分析数据:
①观察以上图表,写出一个结论;
②校团委计划组织志愿服务时间不足10小时的团员参加义务劳动,根据上述信息估计九年级200名团员中参加此次义务劳动的人数约为 人.
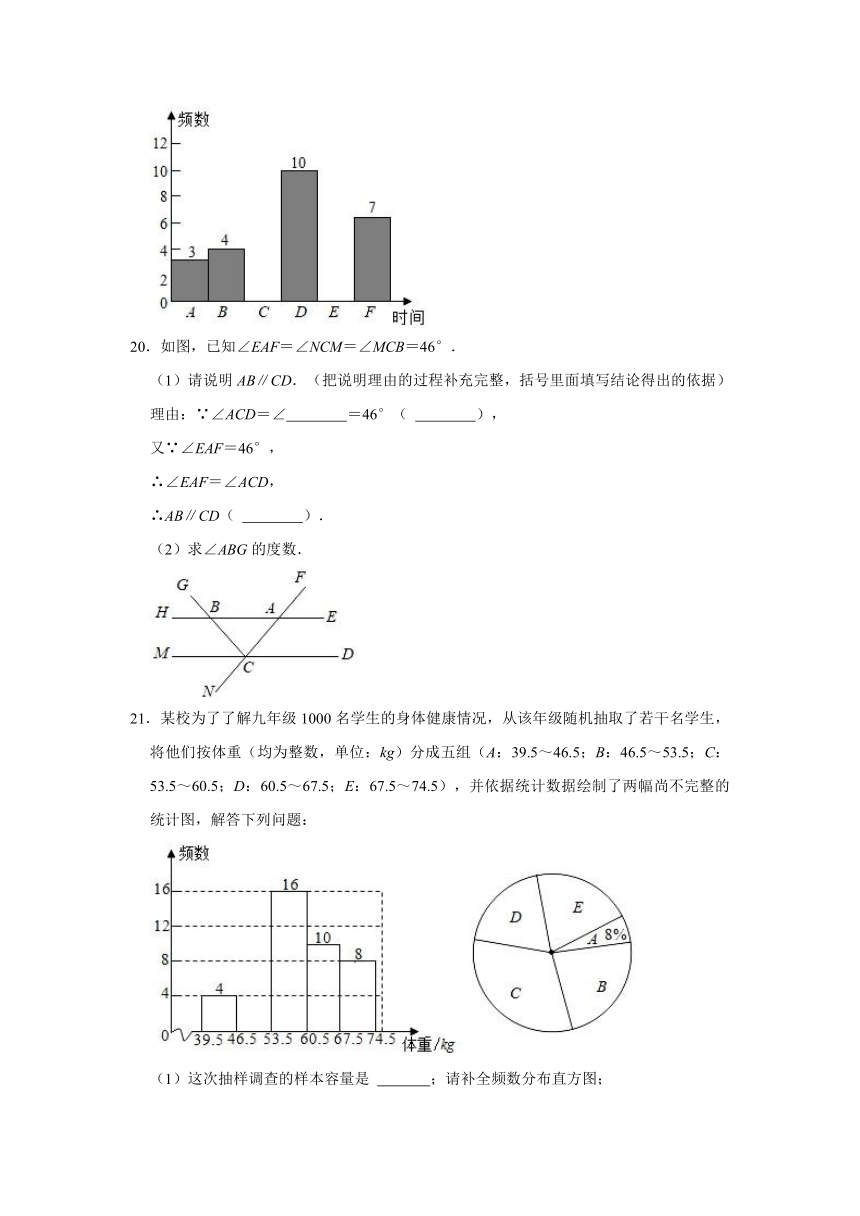
20.如图,已知∠EAF=∠NCM=∠MCB=46°.
(1)请说明AB∥CD.(把说明理由的过程补充完整,括号里面填写结论得出的依据)
理由:∵∠ACD=∠ =46°( ),
又∵∠EAF=46°,
∴∠EAF=∠ACD,
∴AB∥CD( ).
(2)求∠ABG的度数.
21.某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
22.如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
23.汽车行驶时,油箱内的剩余油量V(L)与行驶时间t(h)之间的关系如表:
行驶时间t/h 0 1 2 3 4 5 …
剩余油量V/L 40 35 30 25 20 15 …
(1)油箱内原来有 L油;
(2)行驶5h时,一共用去 L油;
(3)请你写出油箱内的剩余油量V(L)与行驶时间t(h)之间的关系,并指出自变量t的取值范围;
(4)当油箱内的剩余油量是12L时,汽车行驶了多长时间?
24.小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 分才乘上缆车,缆车的平均速度为180米/分.设小亮出发x 分后行走的路程为y 米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是 米,他途中休息了 分.
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度.
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
参考答案
一.选择题(每小题3分,共30分)
1.下列调查中,适合用抽样调查的是( )
A.返校前每个班级学生健康码情况调查
B.对乘坐高铁的乘客进行安检
C.调查一批防疫口罩的质量情况
D.对新研发导弹的零部件进行检查
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
解:A.返校前每个班级学生健康码情况调查,适合全面调查,此选项不符合题意;
B.对乘坐高铁的乘客进行安检,适合全面调查,此选项不符合题意;
C.调查一批防疫口罩的质量情况,适合抽样调查,此选项符合题意;
D.对新研发导弹的零部件进行检查,适合全面调查,此选项不符合题意;
故选:C.
2.世界最大的单口径球面射电望远镜被誉为“中国天眼”,在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒.数据0.00519用科学记数法可以表示为( )
A.5.19×10﹣3 B.5.19×10﹣4 C.5.19×10﹣5 D.5.19×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00519=5.19×10﹣3.
故选:A.
3.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列正确的语句是( )
A.线段PC的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段AC的长是点C到直线PA的距离
【分析】根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短”;“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离”进行判断,即可解答.
解:A.线段PC的长是点C到AP的距离,原说法错误,故此选项不符合题意;
B.PA、PB、PC三条线段中,依据垂线段最短可知PB最短,原说法正确,故此选项符合题意;
C.线段AP的长是点A到直线PC的距离,原说法错误,故此选项不符合题意;
D.线段PC的长是点C到直线PA的距离,原说法错误,故此选项不符合题意;
故选:B.
4.下列运算正确的是( )
A.2x2y+3xy=5x3y2 B.(﹣2ab2)3=﹣6a3b6
C.(3a+b)2=9a2+b2 D.(3a+b)(3a﹣b)=9a2﹣b2
【分析】分别根据合并同类项的法则、积的乘方,完全平方公式以及平方差公式化简即可.
解:A.2x2y和3xy不是同类项,故不能合并,故选项A不合题意;
B.(﹣2ab2)3=﹣8a3b6,故选项B不合题意;
C.(3a+b)2=9a2+6ab+b2,故选项C不合题意;
D.(3a+b)(3a﹣b)=9a2﹣b2,故选项D符合题意.
故选:D.
5.如图,已知AB=10cm,点C在线段AB上,且AC=6cm,点E是线段AC的中点,点D是线段BC的中点.则DE的长为( )
A.4cm B.5cm C.6cm D.7cm
【分析】先计算BC的长度,根据中点可求解CD、EC,再由DE=EC+CD算出DE即可.
解:∵AB=10cm,AC=6cm,
∴BC=AB﹣AC=4cm,
∵点D是线段BC的中点,
∴BD=CD=cm,
∵点E是线段AC的中点,
∴EC==3cm,
∴DE=EC+CD=5(cm).
故选:B.
6.如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2 C.∠B=∠2 D.∠D=∠DCE
【分析】根据平行线的判定方法即可解决问题.
解:∵∠1=∠2,
∴AB∥CD(内错角相等两直线平行),
故选:B.
7.下面说法正确的个数为( )
①过直线外一点有且只有一条直线与已知直线平行;②两直线被第三条直线所截,同旁内角互补;③相等的角是对顶角;④画一条线段的垂线段可以画无数条.
A.1个 B.2个 C.3个 D.4个
【分析】利用平行线的性质定理和判定定理,对顶角的性质解答即可.
解:①过直线外一点有且只有一条直线与已知直线平行,故此选项正确;
②两条平行的直线被第三条直线所截,同旁内角互补,故此选项错误;
③相等的角不一定是对顶角,故此选项错误;
④在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,经过的点不确定,可以画无数条,故此选项正确;
综上所述,正确的个数有2个,
故选:B.
8.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=( )
A.30° B.60° C.90° D.120°
【分析】根据平行线的性质:两条直线平行,内错角相等及角平分线的性质,三角形内角和定理解答.
解:∵AD∥BC,
∴∠ADB=∠B=30°,
再根据角平分线的概念,得:∠BDE=∠ADB=30°,
再根据两条直线平行,内错角相等得:∠DEC=∠ADE=60°,
故选:B.
9.地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km 1 2 3 4
y/℃ 55 90 125 160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为( )
A.5km B.5.5km C.6km D.6.5km
【分析】根据表格中两个变量的数据变化关系,得出函数关系式,再根据函数关系式,当y=230时,求出相应的x的值即可.
解:由表格中数据变化规律可得,当深度每增加1千米,地表以下岩层的温度就升高35℃,
因此有y=55+(90﹣55)(x﹣1),
即y=35x+20,
当y=230时,即35x+20=230,
解得x=6,
故选:C.
10.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
【分析】根据已知信息和函数图象的数据,一次解答每个选项
解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了13﹣8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.
故选:D.
二.填空题(每小题3分,共15分)
11.红树林中学共有学生1600人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了200名学生,其中有60名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有 480 人.
【分析】用总人数乘以样本中最喜欢的项目是跳绳的人数所占比例即可.
解:估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有1600×=480(人),
故答案为:480.
12.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是 82° .
【分析】根据已知条件可直接确定∠AOB的度数.
解:∵OA是表示北偏东60°方向的一条射线,OB是表示南偏东38°方向的一条射线,
∴∠AOB=180°﹣60°﹣38°=82°,
故答案是:82°.
13.已知若x2a=4,x2b=5,则x4a﹣2b= .
【分析】逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可.同底数幂的除法法则:同底数幂相除,底数不变,指数相减.幂的乘方,底数不变,指数相乘.
解:∵x2a=4,x2b=5,
∴x4a﹣2b=(x2a)2÷x2b=42÷5=.
故答案为:.
14.如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在原长方形平面内的点C′和点D′上,若∠1=70°,求∠2的度数为 125° .
【分析】由四边形ABCD是长方形,得到AD∥BC,根据平行线的性质得到∠1=∠C′FB=70°,根据折叠的性质得到∠C′FE=∠EFC=(180°﹣∠C′FB)=(180°﹣70°)=55°,根据平行线的性质即可得到结论.
解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠1=∠C′FB=70°,
∵将长方形纸片ABCD沿直线EF折叠,
∴∠C′FE=∠EFC=(180°﹣∠C′FB)=(180°﹣70°)=55°,
∵AD∥BC,
∴∠2+∠EFC=180°,
∴∠2=180°﹣∠EFC=125°,
故答案为:125°.
15.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数y与n的关系式为 y=n2+2n .
【分析】根据图形的变化规律知,第n个图形的小正方形有(n+1)2﹣1,整理式子即可.
解:由图知,第1个图形中小正方形的个数(1+1)2﹣1=3,
第2个图形中小正方形的个数(2+1)2﹣1=8,
第3个图形中小正方形的个数(3+1)2﹣1=15,
...
第n个图形中小正方形的个数(n+1)2﹣1=y,
故y=(n+1)2﹣1=n2+2n;
故答案为:y=n2+2n.
三、解答题(共9小题)
16.计算.
(1)(3x2y3﹣x3y4)÷(2x2y2).
(2)(a+3b)(2a﹣b).
【分析】(1)直接利用整式的除法运算法则计算得出答案;
(2)直接利用多项式乘多项式运算法则计算得出答案.
解:(1)原式=3x2y3÷2x2y2﹣x3y4÷2x2y2
=;
(2)原式=2a2﹣ab+6ab﹣3b2
=2a2+5ab﹣3b2.
17.先化简,再求值:2x2﹣(2x+3y)(2x﹣3y)﹣(x﹣3y)2,其中x=2,y=.
【分析】原式利用平方差公式,完全平方公式化简,去括号合并得到最简结果,把x与y的值代入计算即可求出值.
解:原式=2x2﹣(4x2﹣9y2)﹣(x2﹣6xy+9y2)
=2x2﹣4x2+9y2﹣x2+6xy﹣9y2
=﹣3x2+6xy,
当x=2,y=时,原式=﹣12+6=﹣6.
18.如图,已知∠MAN,点B在射线AM上,尺规作图:
(1)在AN上取一点C,使AC=BA;
(2)作∠MBD=∠MAN.(保留作图痕迹,不写作法)
【分析】(1)根据要求作出图形即可.
(2)根据要求作出图形即可.
解:(1)如图,线段AC即为所求.
(2)如图,∠MBD即为所求.
19.某学校为了解共青团员志愿服务情况,调查小组根据平台数据进行了抽样问卷调查,过程如下:
(1)从九年级随机抽取40名共青团员,将其志愿服务时间按如下方式分组:A:0~5小时;B:5~10小时;C:10~15小时;D:15~20小时;E:20~25小时;F:25~30小时.(注:每组含最小值,不含最大值)得到这40名志愿者服务时间如下:BDEACEDBFCDDDBECDEEFAFFADCDBDFCFDECEEECE
并将上述数据整理在频数分布表中,请你补充其中的数据.
志愿服务时间 A B C D E F
频数 3 4 7 10 9 7
(2)根据上面的频数分布表,小明绘制了频数分布直方图,请将空缺的部分补充完整;
(3)分析数据:
①观察以上图表,写出一个结论;
②校团委计划组织志愿服务时间不足10小时的团员参加义务劳动,根据上述信息估计九年级200名团员中参加此次义务劳动的人数约为 35 人.
【分析】(1)在40个数据中找出落在C范围的数据即可;
(2)利用(1)中的结果补全频数分布直方图;
(3)①写出一条正确的信息即可;
②用200乘以样本中志愿服务时间不足10小时的团员的百分比即可.
解:(1)由题意知,C的频数为7,
故答案为7;
(2)补全频数分布直方图为:
(3)①九年级共青团员志愿服务时间在15~20小时的人数最多;
②200×=35,
所以估计九年级200名团员中参加此次义务劳动的人数约为35人;
故答案为35;
20.如图,已知∠EAF=∠NCM=∠MCB=46°.
(1)请说明AB∥CD.(把说明理由的过程补充完整,括号里面填写结论得出的依据)
理由:∵∠ACD=∠ NCM =46°( 对顶角相等 ),
又∵∠EAF=46°,
∴∠EAF=∠ACD,
∴AB∥CD( 同位角相等,两直线平行 ).
(2)求∠ABG的度数.
【分析】(1)由对顶角相等可得∠NCM=∠ACD=46°,从而可得∠EAF=∠ACD,可判断AB∥CD;
(2)由平行线的性质可得∠MCB=∠ABC=46°,再由邻补角可求∠ABG的度数.
解:(1)∵∠NCM=∠ACD=46°(对顶角相等),
又∵∠EAF=46°,
∴∠EAF=∠ACD,
∴AB∥CD(同位角相等,两直线平行);
故答案为:NCM;对顶角相等;同位角相等,两直线平行;
(2)∵AB∥CD,
∴∠MCB=∠ABC=46°,
∴∠ABG=180°﹣∠ABC=134°.
21.某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 50 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 72° ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
【分析】(1)根据A组的百分比和频数得出样本容量,并计算出B组的频数补全频数分布直方图即可;
(2)根据直方图中的数据,可以计算出扇形统计图中D组的圆心角的度数;
(3)根据样本估计总体,用九年级学生总数乘以样本中体重超过60kg的学生的频率即可.
解:(1)这次抽样调查的样本容量是4÷8%=50,
B组的频数=50﹣4﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
故答案为:50;
(2)在扇形统计图中D组的圆心角度数是:360°×=72°,
故答案为:72°;
(3)样本中体重超过60kg的学生是10+8=18(名),
估计该校九年级体重超过60kg的学生大约有1000×=360(名).
22.如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
【分析】由角平分线的定义,平行线的性质即可解答.
解:∵AB∥CD,
∴∠B+∠BCE=180°(两直线平行同旁内角互补),
∵∠B=65°,
∴∠BCE=115°,
∵CM平分∠BCE,
∴∠ECM=∠BCE=57.5°,
∵∠ECM+∠MCN+∠NCD=180°,∠MCN=90°,
∴∠NCD=180°﹣∠ECM﹣∠MCN=180°﹣57.5°﹣90°=32.5°.
23.汽车行驶时,油箱内的剩余油量V(L)与行驶时间t(h)之间的关系如表:
行驶时间t/h 0 1 2 3 4 5 …
剩余油量V/L 40 35 30 25 20 15 …
(1)油箱内原来有 40 L油;
(2)行驶5h时,一共用去 25 L油;
(3)请你写出油箱内的剩余油量V(L)与行驶时间t(h)之间的关系,并指出自变量t的取值范围;
(4)当油箱内的剩余油量是12L时,汽车行驶了多长时间?
【分析】(1)根据观察表格,可得答案;
(2)根据总的油量减去剩余油量,可得答案;
(3)根据总的油量减去用油量,可得函数关系式,根据总油量与每小时的耗油量,可得t的取值范围;
(4)根据函数值,可得相应的自变量的值.
解:(1)行驶0小时,即没耗油,得出油箱内原来有 40L油,
(2)行驶5小时剩余油量是15L,
5小时的用油量是40﹣15=25(L),
故答案为:40,25;
(3)每小时用油5L,剩余油量与行驶时间之间的关系是V=40﹣5t (0≤t≤8),
(4)当V=12时,12=40﹣5t
t=5.6(小时),
答:汽车行驶了5.6小时.
24.小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 分才乘上缆车,缆车的平均速度为180米/分.设小亮出发x 分后行走的路程为y 米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是 3600 米,他途中休息了 20 分.
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度.
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
解:(1)根据图象知:小亮行走的总路程是 3600米,他途中休息了 20分钟.
故答案为 3600,20; …
(2)小亮休息前的速度为:(米/分)
小亮休息后的速度为:(米/分)
(3)小颖所用时间:(分)
小亮比小颖迟到80﹣50﹣10=20(分)
∴小颖到达终点时,小亮离缆车终点的路程为:20×55=1100(米)
一.选择题(共10小题,每题3分,共30分).
1.下列调查中,适合用抽样调查的是( )
A.返校前每个班级学生健康码情况调查
B.对乘坐高铁的乘客进行安检
C.调查一批防疫口罩的质量情况
D.对新研发导弹的零部件进行检查
2.世界最大的单口径球面射电望远镜被誉为“中国天眼”,在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒.数据0.00519用科学记数法可以表示为( )
A.5.19×10﹣3 B.5.19×10﹣4 C.5.19×10﹣5 D.5.19×10﹣6
3.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列正确的语句是( )
A.线段PC的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段AC的长是点C到直线PA的距离
4.下列运算正确的是( )
A.2x2y+3xy=5x3y2 B.(﹣2ab2)3=﹣6a3b6
C.(3a+b)2=9a2+b2 D.(3a+b)(3a﹣b)=9a2﹣b2
5.如图,已知AB=10cm,点C在线段AB上,且AC=6cm,点E是线段AC的中点,点D是线段BC的中点.则DE的长为( )
A.4cm B.5cm C.6cm D.7cm
6.如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2 C.∠B=∠2 D.∠D=∠DCE
7.下面说法正确的个数为( )
①过直线外一点有且只有一条直线与已知直线平行;②两直线被第三条直线所截,同旁内角互补;③相等的角是对顶角;④画一条线段的垂线段可以画无数条.
A.1个 B.2个 C.3个 D.4个
8.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=( )
A.30° B.60° C.90° D.120°
9.地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km 1 2 3 4
y/℃ 55 90 125 160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为( )
A.5km B.5.5km C.6km D.6.5km
10.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
二.填空题(每小题3分,共15分)
11.红树林中学共有学生1600人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了200名学生,其中有60名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有 人.
12.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是 .
13.已知若x2a=4,x2b=5,则x4a﹣2b= .
14.如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在原长方形平面内的点C′和点D′上,若∠1=70°,求∠2的度数为 .
15.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数y与n的关系式为 .
三、解答题(共9小题)
16.计算.
(1)(3x2y3﹣x3y4)÷(2x2y2).
(2)(a+3b)(2a﹣b).
17.先化简,再求值:2x2﹣(2x+3y)(2x﹣3y)﹣(x﹣3y)2,其中x=2,y=.
18.如图,已知∠MAN,点B在射线AM上,尺规作图:
(1)在AN上取一点C,使AC=BA;
(2)作∠MBD=∠MAN.(保留作图痕迹,不写作法)
19.某学校为了解共青团员志愿服务情况,调查小组根据平台数据进行了抽样问卷调查,过程如下:
(1)从九年级随机抽取40名共青团员,将其志愿服务时间按如下方式分组:A:0~5小时;B:5~10小时;C:10~15小时;D:15~20小时;E:20~25小时;F:25~30小时.(注:每组含最小值,不含最大值)得到这40名志愿者服务时间如下:BDEACEDBFCDDDBECDEEFAFFADCDBDFCFDECEEECE
并将上述数据整理在频数分布表中,请你补充其中的数据.
志愿服务时间 A B C D E F
频数 3 4 10 9 7
(2)根据上面的频数分布表,小明绘制了频数分布直方图,请将空缺的部分补充完整;
(3)分析数据:
①观察以上图表,写出一个结论;
②校团委计划组织志愿服务时间不足10小时的团员参加义务劳动,根据上述信息估计九年级200名团员中参加此次义务劳动的人数约为 人.
20.如图,已知∠EAF=∠NCM=∠MCB=46°.
(1)请说明AB∥CD.(把说明理由的过程补充完整,括号里面填写结论得出的依据)
理由:∵∠ACD=∠ =46°( ),
又∵∠EAF=46°,
∴∠EAF=∠ACD,
∴AB∥CD( ).
(2)求∠ABG的度数.
21.某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
22.如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
23.汽车行驶时,油箱内的剩余油量V(L)与行驶时间t(h)之间的关系如表:
行驶时间t/h 0 1 2 3 4 5 …
剩余油量V/L 40 35 30 25 20 15 …
(1)油箱内原来有 L油;
(2)行驶5h时,一共用去 L油;
(3)请你写出油箱内的剩余油量V(L)与行驶时间t(h)之间的关系,并指出自变量t的取值范围;
(4)当油箱内的剩余油量是12L时,汽车行驶了多长时间?
24.小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 分才乘上缆车,缆车的平均速度为180米/分.设小亮出发x 分后行走的路程为y 米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是 米,他途中休息了 分.
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度.
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
参考答案
一.选择题(每小题3分,共30分)
1.下列调查中,适合用抽样调查的是( )
A.返校前每个班级学生健康码情况调查
B.对乘坐高铁的乘客进行安检
C.调查一批防疫口罩的质量情况
D.对新研发导弹的零部件进行检查
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
解:A.返校前每个班级学生健康码情况调查,适合全面调查,此选项不符合题意;
B.对乘坐高铁的乘客进行安检,适合全面调查,此选项不符合题意;
C.调查一批防疫口罩的质量情况,适合抽样调查,此选项符合题意;
D.对新研发导弹的零部件进行检查,适合全面调查,此选项不符合题意;
故选:C.
2.世界最大的单口径球面射电望远镜被誉为“中国天眼”,在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒.数据0.00519用科学记数法可以表示为( )
A.5.19×10﹣3 B.5.19×10﹣4 C.5.19×10﹣5 D.5.19×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00519=5.19×10﹣3.
故选:A.
3.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列正确的语句是( )
A.线段PC的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段AC的长是点C到直线PA的距离
【分析】根据“从直线外一点到这条直线上各点所连的线段中,垂线段最短”;“从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离”进行判断,即可解答.
解:A.线段PC的长是点C到AP的距离,原说法错误,故此选项不符合题意;
B.PA、PB、PC三条线段中,依据垂线段最短可知PB最短,原说法正确,故此选项符合题意;
C.线段AP的长是点A到直线PC的距离,原说法错误,故此选项不符合题意;
D.线段PC的长是点C到直线PA的距离,原说法错误,故此选项不符合题意;
故选:B.
4.下列运算正确的是( )
A.2x2y+3xy=5x3y2 B.(﹣2ab2)3=﹣6a3b6
C.(3a+b)2=9a2+b2 D.(3a+b)(3a﹣b)=9a2﹣b2
【分析】分别根据合并同类项的法则、积的乘方,完全平方公式以及平方差公式化简即可.
解:A.2x2y和3xy不是同类项,故不能合并,故选项A不合题意;
B.(﹣2ab2)3=﹣8a3b6,故选项B不合题意;
C.(3a+b)2=9a2+6ab+b2,故选项C不合题意;
D.(3a+b)(3a﹣b)=9a2﹣b2,故选项D符合题意.
故选:D.
5.如图,已知AB=10cm,点C在线段AB上,且AC=6cm,点E是线段AC的中点,点D是线段BC的中点.则DE的长为( )
A.4cm B.5cm C.6cm D.7cm
【分析】先计算BC的长度,根据中点可求解CD、EC,再由DE=EC+CD算出DE即可.
解:∵AB=10cm,AC=6cm,
∴BC=AB﹣AC=4cm,
∵点D是线段BC的中点,
∴BD=CD=cm,
∵点E是线段AC的中点,
∴EC==3cm,
∴DE=EC+CD=5(cm).
故选:B.
6.如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2 C.∠B=∠2 D.∠D=∠DCE
【分析】根据平行线的判定方法即可解决问题.
解:∵∠1=∠2,
∴AB∥CD(内错角相等两直线平行),
故选:B.
7.下面说法正确的个数为( )
①过直线外一点有且只有一条直线与已知直线平行;②两直线被第三条直线所截,同旁内角互补;③相等的角是对顶角;④画一条线段的垂线段可以画无数条.
A.1个 B.2个 C.3个 D.4个
【分析】利用平行线的性质定理和判定定理,对顶角的性质解答即可.
解:①过直线外一点有且只有一条直线与已知直线平行,故此选项正确;
②两条平行的直线被第三条直线所截,同旁内角互补,故此选项错误;
③相等的角不一定是对顶角,故此选项错误;
④在同一平面内,经过一点能画一条且只能画一条直线与已知直线垂直,经过的点不确定,可以画无数条,故此选项正确;
综上所述,正确的个数有2个,
故选:B.
8.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC=( )
A.30° B.60° C.90° D.120°
【分析】根据平行线的性质:两条直线平行,内错角相等及角平分线的性质,三角形内角和定理解答.
解:∵AD∥BC,
∴∠ADB=∠B=30°,
再根据角平分线的概念,得:∠BDE=∠ADB=30°,
再根据两条直线平行,内错角相等得:∠DEC=∠ADE=60°,
故选:B.
9.地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间有如下关系:
x/km 1 2 3 4
y/℃ 55 90 125 160
根据表格,估计地表以下岩层的温度为230℃时,岩层所处的深度为( )
A.5km B.5.5km C.6km D.6.5km
【分析】根据表格中两个变量的数据变化关系,得出函数关系式,再根据函数关系式,当y=230时,求出相应的x的值即可.
解:由表格中数据变化规律可得,当深度每增加1千米,地表以下岩层的温度就升高35℃,
因此有y=55+(90﹣55)(x﹣1),
即y=35x+20,
当y=230时,即35x+20=230,
解得x=6,
故选:C.
10.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
【分析】根据已知信息和函数图象的数据,一次解答每个选项
解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了13﹣8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.
故选:D.
二.填空题(每小题3分,共15分)
11.红树林中学共有学生1600人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了200名学生,其中有60名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有 480 人.
【分析】用总人数乘以样本中最喜欢的项目是跳绳的人数所占比例即可.
解:估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有1600×=480(人),
故答案为:480.
12.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东60°的方向上,观测到小岛B在它南偏东38°的方向上,则∠AOB的度数是 82° .
【分析】根据已知条件可直接确定∠AOB的度数.
解:∵OA是表示北偏东60°方向的一条射线,OB是表示南偏东38°方向的一条射线,
∴∠AOB=180°﹣60°﹣38°=82°,
故答案是:82°.
13.已知若x2a=4,x2b=5,则x4a﹣2b= .
【分析】逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可.同底数幂的除法法则:同底数幂相除,底数不变,指数相减.幂的乘方,底数不变,指数相乘.
解:∵x2a=4,x2b=5,
∴x4a﹣2b=(x2a)2÷x2b=42÷5=.
故答案为:.
14.如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在原长方形平面内的点C′和点D′上,若∠1=70°,求∠2的度数为 125° .
【分析】由四边形ABCD是长方形,得到AD∥BC,根据平行线的性质得到∠1=∠C′FB=70°,根据折叠的性质得到∠C′FE=∠EFC=(180°﹣∠C′FB)=(180°﹣70°)=55°,根据平行线的性质即可得到结论.
解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠1=∠C′FB=70°,
∵将长方形纸片ABCD沿直线EF折叠,
∴∠C′FE=∠EFC=(180°﹣∠C′FB)=(180°﹣70°)=55°,
∵AD∥BC,
∴∠2+∠EFC=180°,
∴∠2=180°﹣∠EFC=125°,
故答案为:125°.
15.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数y与n的关系式为 y=n2+2n .
【分析】根据图形的变化规律知,第n个图形的小正方形有(n+1)2﹣1,整理式子即可.
解:由图知,第1个图形中小正方形的个数(1+1)2﹣1=3,
第2个图形中小正方形的个数(2+1)2﹣1=8,
第3个图形中小正方形的个数(3+1)2﹣1=15,
...
第n个图形中小正方形的个数(n+1)2﹣1=y,
故y=(n+1)2﹣1=n2+2n;
故答案为:y=n2+2n.
三、解答题(共9小题)
16.计算.
(1)(3x2y3﹣x3y4)÷(2x2y2).
(2)(a+3b)(2a﹣b).
【分析】(1)直接利用整式的除法运算法则计算得出答案;
(2)直接利用多项式乘多项式运算法则计算得出答案.
解:(1)原式=3x2y3÷2x2y2﹣x3y4÷2x2y2
=;
(2)原式=2a2﹣ab+6ab﹣3b2
=2a2+5ab﹣3b2.
17.先化简,再求值:2x2﹣(2x+3y)(2x﹣3y)﹣(x﹣3y)2,其中x=2,y=.
【分析】原式利用平方差公式,完全平方公式化简,去括号合并得到最简结果,把x与y的值代入计算即可求出值.
解:原式=2x2﹣(4x2﹣9y2)﹣(x2﹣6xy+9y2)
=2x2﹣4x2+9y2﹣x2+6xy﹣9y2
=﹣3x2+6xy,
当x=2,y=时,原式=﹣12+6=﹣6.
18.如图,已知∠MAN,点B在射线AM上,尺规作图:
(1)在AN上取一点C,使AC=BA;
(2)作∠MBD=∠MAN.(保留作图痕迹,不写作法)
【分析】(1)根据要求作出图形即可.
(2)根据要求作出图形即可.
解:(1)如图,线段AC即为所求.
(2)如图,∠MBD即为所求.
19.某学校为了解共青团员志愿服务情况,调查小组根据平台数据进行了抽样问卷调查,过程如下:
(1)从九年级随机抽取40名共青团员,将其志愿服务时间按如下方式分组:A:0~5小时;B:5~10小时;C:10~15小时;D:15~20小时;E:20~25小时;F:25~30小时.(注:每组含最小值,不含最大值)得到这40名志愿者服务时间如下:BDEACEDBFCDDDBECDEEFAFFADCDBDFCFDECEEECE
并将上述数据整理在频数分布表中,请你补充其中的数据.
志愿服务时间 A B C D E F
频数 3 4 7 10 9 7
(2)根据上面的频数分布表,小明绘制了频数分布直方图,请将空缺的部分补充完整;
(3)分析数据:
①观察以上图表,写出一个结论;
②校团委计划组织志愿服务时间不足10小时的团员参加义务劳动,根据上述信息估计九年级200名团员中参加此次义务劳动的人数约为 35 人.
【分析】(1)在40个数据中找出落在C范围的数据即可;
(2)利用(1)中的结果补全频数分布直方图;
(3)①写出一条正确的信息即可;
②用200乘以样本中志愿服务时间不足10小时的团员的百分比即可.
解:(1)由题意知,C的频数为7,
故答案为7;
(2)补全频数分布直方图为:
(3)①九年级共青团员志愿服务时间在15~20小时的人数最多;
②200×=35,
所以估计九年级200名团员中参加此次义务劳动的人数约为35人;
故答案为35;
20.如图,已知∠EAF=∠NCM=∠MCB=46°.
(1)请说明AB∥CD.(把说明理由的过程补充完整,括号里面填写结论得出的依据)
理由:∵∠ACD=∠ NCM =46°( 对顶角相等 ),
又∵∠EAF=46°,
∴∠EAF=∠ACD,
∴AB∥CD( 同位角相等,两直线平行 ).
(2)求∠ABG的度数.
【分析】(1)由对顶角相等可得∠NCM=∠ACD=46°,从而可得∠EAF=∠ACD,可判断AB∥CD;
(2)由平行线的性质可得∠MCB=∠ABC=46°,再由邻补角可求∠ABG的度数.
解:(1)∵∠NCM=∠ACD=46°(对顶角相等),
又∵∠EAF=46°,
∴∠EAF=∠ACD,
∴AB∥CD(同位角相等,两直线平行);
故答案为:NCM;对顶角相等;同位角相等,两直线平行;
(2)∵AB∥CD,
∴∠MCB=∠ABC=46°,
∴∠ABG=180°﹣∠ABC=134°.
21.某校为了了解九年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了两幅尚不完整的统计图,解答下列问题:
(1)这次抽样调查的样本容量是 50 ;请补全频数分布直方图;
(2)在扇形统计图中D组的圆心角度数是 72° ;
(3)请你估计该校九年级体重超过60kg的学生大约有多少名?
【分析】(1)根据A组的百分比和频数得出样本容量,并计算出B组的频数补全频数分布直方图即可;
(2)根据直方图中的数据,可以计算出扇形统计图中D组的圆心角的度数;
(3)根据样本估计总体,用九年级学生总数乘以样本中体重超过60kg的学生的频率即可.
解:(1)这次抽样调查的样本容量是4÷8%=50,
B组的频数=50﹣4﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
故答案为:50;
(2)在扇形统计图中D组的圆心角度数是:360°×=72°,
故答案为:72°;
(3)样本中体重超过60kg的学生是10+8=18(名),
估计该校九年级体重超过60kg的学生大约有1000×=360(名).
22.如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
【分析】由角平分线的定义,平行线的性质即可解答.
解:∵AB∥CD,
∴∠B+∠BCE=180°(两直线平行同旁内角互补),
∵∠B=65°,
∴∠BCE=115°,
∵CM平分∠BCE,
∴∠ECM=∠BCE=57.5°,
∵∠ECM+∠MCN+∠NCD=180°,∠MCN=90°,
∴∠NCD=180°﹣∠ECM﹣∠MCN=180°﹣57.5°﹣90°=32.5°.
23.汽车行驶时,油箱内的剩余油量V(L)与行驶时间t(h)之间的关系如表:
行驶时间t/h 0 1 2 3 4 5 …
剩余油量V/L 40 35 30 25 20 15 …
(1)油箱内原来有 40 L油;
(2)行驶5h时,一共用去 25 L油;
(3)请你写出油箱内的剩余油量V(L)与行驶时间t(h)之间的关系,并指出自变量t的取值范围;
(4)当油箱内的剩余油量是12L时,汽车行驶了多长时间?
【分析】(1)根据观察表格,可得答案;
(2)根据总的油量减去剩余油量,可得答案;
(3)根据总的油量减去用油量,可得函数关系式,根据总油量与每小时的耗油量,可得t的取值范围;
(4)根据函数值,可得相应的自变量的值.
解:(1)行驶0小时,即没耗油,得出油箱内原来有 40L油,
(2)行驶5小时剩余油量是15L,
5小时的用油量是40﹣15=25(L),
故答案为:40,25;
(3)每小时用油5L,剩余油量与行驶时间之间的关系是V=40﹣5t (0≤t≤8),
(4)当V=12时,12=40﹣5t
t=5.6(小时),
答:汽车行驶了5.6小时.
24.小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 分才乘上缆车,缆车的平均速度为180米/分.设小亮出发x 分后行走的路程为y 米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是 3600 米,他途中休息了 20 分.
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度.
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
解:(1)根据图象知:小亮行走的总路程是 3600米,他途中休息了 20分钟.
故答案为 3600,20; …
(2)小亮休息前的速度为:(米/分)
小亮休息后的速度为:(米/分)
(3)小颖所用时间:(分)
小亮比小颖迟到80﹣50﹣10=20(分)
∴小颖到达终点时,小亮离缆车终点的路程为:20×55=1100(米)
同课章节目录
