2020-2021学年山东省淄博市周村区八年级(下)期末数学试卷(五四学制)(Word版含解析)
文档属性
| 名称 | 2020-2021学年山东省淄博市周村区八年级(下)期末数学试卷(五四学制)(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 07:55:37 | ||
图片预览


文档简介
2020-2021学年山东省淄博市周村区八年级(下)期末数学试卷(五四学制)
一、选择题(每小题4分,共48分).
1.下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.式子在实数范围内有意义,则x的取值范围是( )
A.x<3 B.x≥3 C.x≤3 D.x>3
3.下列各式中,运算正确的是( )
A. B. C. D.
4.如果3x=4y(y≠0),那么下列比例式中正确的是( )
A. B. C. D.
5.用配方法解方程x2﹣4x﹣1=0,方程应变形为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.(x﹣2)2=5
6.关于x的一元二次方程(k+1)x2+2x=0有两个不相等的实数根,则k的取值范围为( )
A.k>﹣1 B.k<﹣1 C.k≠﹣1 D.k<0且k≠﹣1
7.如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法判断
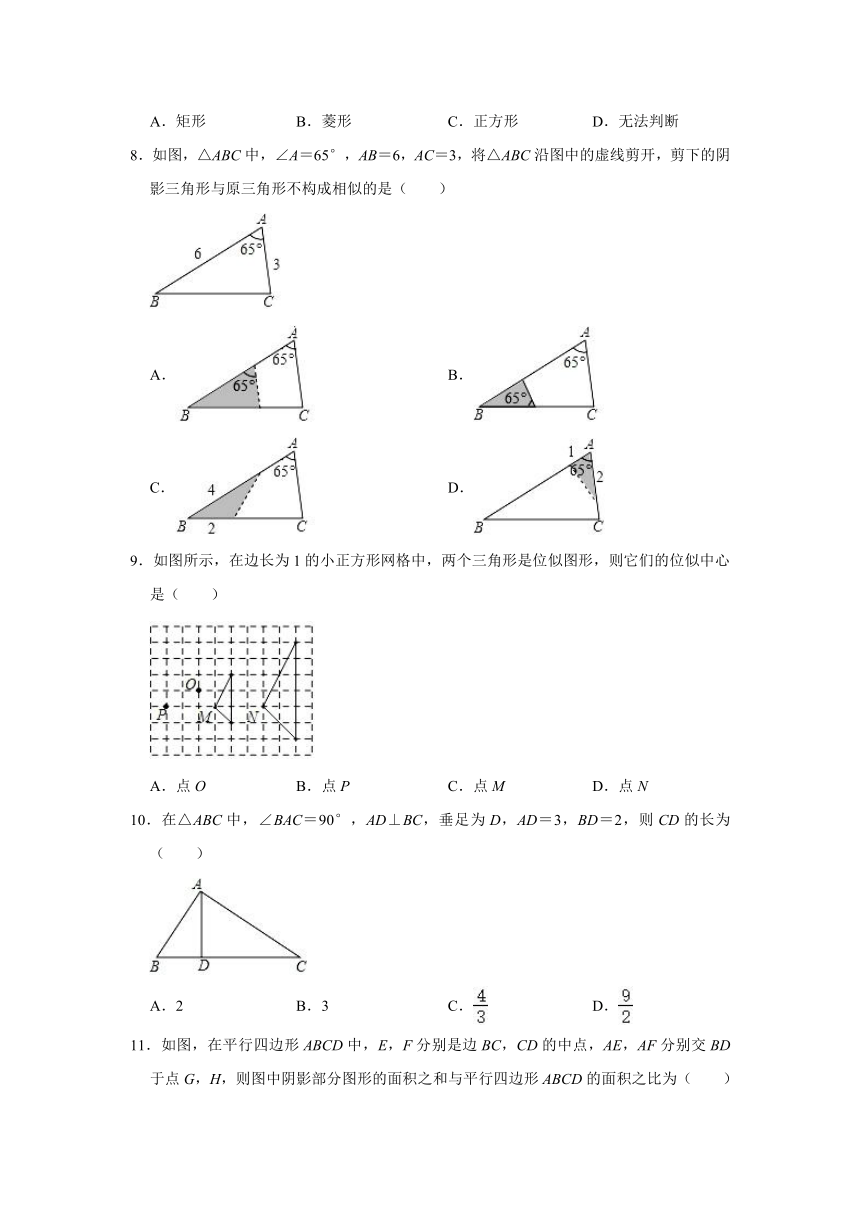
8.如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
9.如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是( )
A.点O B.点P C.点M D.点N
10.在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,BD=2,则CD的长为( )
A.2 B.3 C. D.
11.如图,在平行四边形ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,则图中阴影部分图形的面积之和与平行四边形ABCD的面积之比为( )
A. B. C. D.
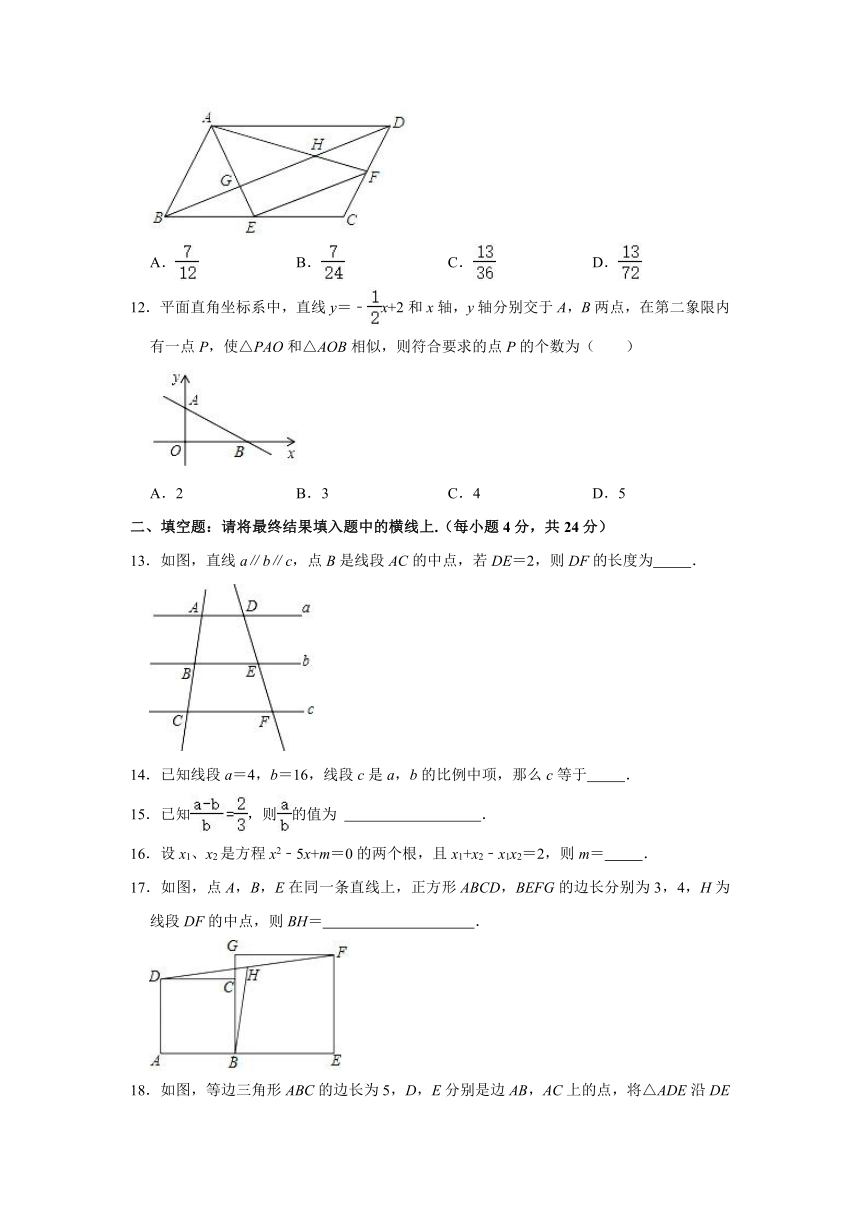
12.平面直角坐标系中,直线y=﹣x+2和x轴,y轴分别交于A,B两点,在第二象限内有一点P,使△PAO和△AOB相似,则符合要求的点P的个数为( )
A.2 B.3 C.4 D.5
二、填空题:请将最终结果填入题中的横线上.(每小题4分,共24分)
13.如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则DF的长度为 .
14.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 .
15.已知,则的值为 .
16.设x1、x2是方程x2﹣5x+m=0的两个根,且x1+x2﹣x1x2=2,则m= .
17.如图,点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为3,4,H为线段DF的中点,则BH= .
18.如图,等边三角形ABC的边长为5,D,E分别是边AB,AC上的点,将△ADE沿DE折叠,点A恰好落在BC边上的点F处,若BF=2,则BD的长是 .
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共78分)
19.已知a=+1,求代数式a2﹣2a+7的值.
20.解方程:(x﹣7)2﹣3x(7﹣x)=0.
21.如图,在△ABC中,点D,E分别在边AB,AC上,连接DE,且AD?AB=AE?AC.
(1)求证:△ADE∽△ACB;
(2)若∠B=55°,∠ADE=75°,求∠A的度数.
22.关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
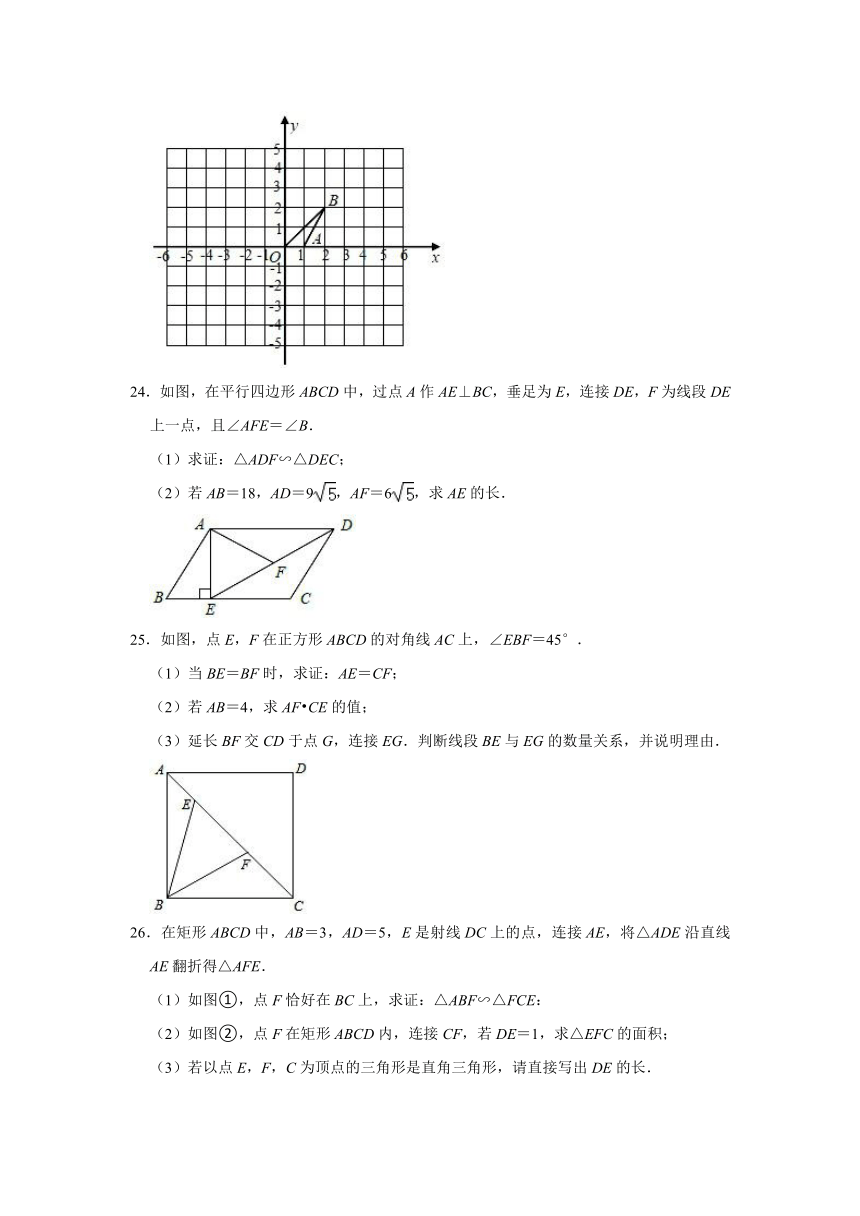
23.如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
24.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=18,AD=9,AF=6,求AE的长.
25.如图,点E,F在正方形ABCD的对角线AC上,∠EBF=45°.
(1)当BE=BF时,求证:AE=CF;
(2)若AB=4,求AF?CE的值;
(3)延长BF交CD于点G,连接EG.判断线段BE与EG的数量关系,并说明理由.
26.在矩形ABCD中,AB=3,AD=5,E是射线DC上的点,连接AE,将△ADE沿直线AE翻折得△AFE.
(1)如图①,点F恰好在BC上,求证:△ABF∽△FCE:
(2)如图②,点F在矩形ABCD内,连接CF,若DE=1,求△EFC的面积;
(3)若以点E,F,C为顶点的三角形是直角三角形,请直接写出DE的长.
参考答案
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共48分)
1.下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形以及轴对称图形的概念对各选项分析判断即可.
解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.不是轴对称图形,是中心对称图形,故本选项不合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.是轴对称图形,不是中心对称图形,故本选项不合题意.
故选:A.
2.式子在实数范围内有意义,则x的取值范围是( )
A.x<3 B.x≥3 C.x≤3 D.x>3
【分析】直接利用二次根式有意义的条件分析得出答案.
解:式子在实数范围内有意义,故x﹣3≥0,
则x的取值范围是:x≥3.
故选:B.
3.下列各式中,运算正确的是( )
A. B. C. D.
【分析】直接利用二次根式的性质分别化简计算得出答案.
解:A、=2,正确;
B、3﹣=2,故此选项错误;
C、2+,无法计算,故此选项错误;
D、=2,故此选项错误.
故选:A.
4.如果3x=4y(y≠0),那么下列比例式中正确的是( )
A. B. C. D.
【分析】根据比例的性质,可得答案.
解:A、由比例的性质,得4x=3y与3x=4y不一致,故A不符合题意;
B、由比例的性质,得xy=12与3x=4y不一致,故B不符合题意;
C、由比例的性质,得4x=3y与3x=4y不一致,故C不符合题意;
D、由比例的性质,得3x=4y与3x=4y一致,故D符合题意;
故选:D.
5.用配方法解方程x2﹣4x﹣1=0,方程应变形为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.(x﹣2)2=5
【分析】常数项移到方程的右边后,两边配上一次项系数一半的平方,写成完全平方式即可得.
解:∵x2﹣4x=1,
∴x2﹣4x+4=1+4,即(x﹣2)2=5,
故选:D.
6.关于x的一元二次方程(k+1)x2+2x=0有两个不相等的实数根,则k的取值范围为( )
A.k>﹣1 B.k<﹣1 C.k≠﹣1 D.k<0且k≠﹣1
【分析】根据根的判别式和一元二方程的定义得出△=22﹣4(k+1)×0>0且k+1≠0,求出即可.
解:∵关于x的一元二次方程(k+1)x2+2x=0有两个不相等的实数根,
∴△=22﹣4(k+1)×0>0且k+1≠0,
解得:k≠﹣1,
故选:C.
7.如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法判断
【分析】由条件可知AB∥CD,AD∥BC,再证明AB=BC即可解决问题.
解:过点D作DE⊥AB于E,DF⊥BC于F.
∵两直尺的宽度相等,
∴DE=DF.
又∵平行四边形ABCD的面积=AB?DE=BC?DF,
∴AB=BC,
∴平行四边形ABCD为菱形.
故选:B.
8.如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
【分析】根据相似三角形的判定定理对各选项进行逐一判定即可.
解:A、根据平行线截得的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
C、两三角形的对应角不一定相等,故两三角形不相似,故本选项符合题意;
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项不符合题意.
故选:C.
9.如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是( )
A.点O B.点P C.点M D.点N
【分析】直接利用位似图形的性质进而连接对应点得出位似中心即可.
解:如图所示:两个三角形的位似中心是:点P.
故选:B.
10.在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,BD=2,则CD的长为( )
A.2 B.3 C. D.
【分析】证明△BDA∽△ADC,根据相似三角形的性质列出比例式,把已知数据代入计算,得到答案.
解:∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵AD⊥BC,
∴∠C+∠CAD=90°,
∴∠C=∠BAD,
∵∠BDA=∠ADC=90°,
∴△BDA∽△ADC,
∴,
即,
解得,DC=,
故选:D.
11.如图,在平行四边形ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,则图中阴影部分图形的面积之和与平行四边形ABCD的面积之比为( )
A. B. C. D.
【分析】依据相似三角形的对应边成比例,即可得到GH=BD,进而得出S△AGH=S△ABD=S四边形ABCD;依据三角形中位线定理,即可得到S△CEF=S△BCD=S四边形ABCD,据此可得阴影部分图形的面积与?ABCD的面积之比.
解:∵BE∥AD,E是BC的中点,
∴△BEG∽△DAG,
∴,即BG=BD,
同理可得,DH=BD,
∴GH=BD,
∴S△AGH=S△ABD=S四边形ABCD,
∵E、F分别是边BC、CD的中点,
∴EF∥BD,EF=BD,
∴△CEF∽△CBD,
∴,
∴S△CEF=S△BCD=S四边形ABCD,,
∴图中阴影部分图形的面积=()S四边形ABCD=S四边形ABCD,
即图中阴影部分图形的面积与?ABCD的面积之比为=7:24,
故选:B.
12.平面直角坐标系中,直线y=﹣x+2和x轴,y轴分别交于A,B两点,在第二象限内有一点P,使△PAO和△AOB相似,则符合要求的点P的个数为( )
A.2 B.3 C.4 D.5
【分析】根据相似三角形的相似条件,画出图形即可解决问题.
解:如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选:C.
二、填空题:请将最终结果填入题中的横线上.(每小题4分,共24分)
13.如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则DF的长度为 4 .
【分析】先求出AB=BC,根据平行线分线段成比例定理得出比例式,代入即可求出EF,再求出DF即可.
解:∵点B是线段AC的中点,
∴AB=BC,
∴=1,
∵直线a∥b∥c,
∴==1,
∵DE=2,
∴EF=2,
∴DF=DE+EF=2+2=4,
故答案为:4.
14.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 8 .
【分析】根据线段比例中项的概念a:c=c:b,可得c2=ab=64,即可求出c的值.
解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得:c=±8,
又∵线段是正数,
∴c=8.
故答案为:8.
15.已知,则的值为 .
【分析】直接利用已知将原式变形进而得出答案.
解:∵,
∴3a﹣3b=2b,
故3a=5b,
∴的值为:.
故答案为:.
16.设x1、x2是方程x2﹣5x+m=0的两个根,且x1+x2﹣x1x2=2,则m= 3 .
【分析】由根与系数的关系可得x1+x2=5、x1x2=m,结合x1+x2﹣x1x2=2可得出关于m的一元一次方程,解之即可得出结论.
解:∵x1、x2是方程x2﹣5x+m=0的两个根,
∴x1+x2=5,x1x2=m.
∵x1+x2﹣x1x2=5﹣m=2,
∴m=3.
故答案为:3.
17.如图,点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为3,4,H为线段DF的中点,则BH= .
【分析】作辅助线,连接BD,BF,可得三角形DBF为直角三角形,求出DF,根据直角三角形斜边中线可得结论.
解:连接BD、BF,
∵四边形ABCD,BEFG是正方形,且边长分别为3和4,
∴∠DBC=∠GBF=45°,BD=3,BF=4,
∴∠DBF=90°,
由勾股定理得:DF==5,
∵H为线段DF的中点,
∴BH=DF=.
故答案为:.
18.如图,等边三角形ABC的边长为5,D,E分别是边AB,AC上的点,将△ADE沿DE折叠,点A恰好落在BC边上的点F处,若BF=2,则BD的长是 .
【分析】根据翻转变换的性质可知,DA=DF,EA=EF,∠DFE=∠A=60°,利用相似三角形△DBF∽△FCE,对应边成比例,列方程求解即可.
解:∵等边三角形ABC的边长为5,BF=2,
∴FC=5﹣2=3,AB=BC=AC=5,∠A=∠B=∠C=60°,
由翻转变换的性质可知,DA=DF,EA=EF,∠DFE=∠A=60°,
∵∠DFC=∠BDF+∠B,即∠DFE+∠EFC=∠BDF+∠B,
∴∠BDF=∠CFE,
又∵∠B=∠C=60°,
∴△DBF∽△FCE,
∴==,
设BD=x,则AD=5﹣x=DF,
即==,
∴EC=,FE=,
又∵EC+EF=EC+EA=AC=5,
∴+=5,
解得x=,
经检验x=是方程的解,
∴BD=,
故答案为:.
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共78分)
19.已知a=+1,求代数式a2﹣2a+7的值.
【分析】将a的值代入a2﹣2a+7=(a﹣1)2+6计算可得.
解:a2﹣2a+7=(a﹣1)2+6,
当时,
原式=(+1﹣1)2+6
=5+6
=11.
20.解方程:(x﹣7)2﹣3x(7﹣x)=0.
【分析】将方程左边多项式第二项提取﹣1变形后,提取公因式x﹣7化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解:方程变形得:(x﹣7)2+3x(x﹣7)=0,
分解因式得:(x﹣7)(x﹣7+3x)=0,即(x﹣7)(4x﹣7)=0,
可得x﹣7=0或4x﹣7=0,
∴x1=7,x2=.
21.如图,在△ABC中,点D,E分别在边AB,AC上,连接DE,且AD?AB=AE?AC.
(1)求证:△ADE∽△ACB;
(2)若∠B=55°,∠ADE=75°,求∠A的度数.
【分析】(1)本题根据相似三角形的判定可以推出△ADE∽△ACB.
(2)由第(1)问可知△ADE∽△ACB,进而得到∠ADE=∠ACB,从而得到∠ACB=75°,在利用三角形的内角和得出所求角即可.
【解答】(1)证明:
∵AD?AB=AE?AC,
∴.
又∵∠A=∠A,
∴△ADE∽△ACB.
(2)解:由(1)知,△ADE∽△ACB,
∴∠ADE=∠ACB.
∵∠ADE=75°,
∴∠ACB=75°.
又∵∠B=55°,
∴∠A=180°﹣∠ACB﹣∠B=50°.
22.关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
【分析】(1)由方程根的情况,根据根的判别式可得到关于m的方程,则可求得m的取值范围;
(2)由(1)中所求m的取值范围,取一个m的值,代入方程求解即可.
解:(1)∵关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个不相等的实数根,
∴△>0,即(﹣2m)2﹣4(m﹣1)2=8m﹣4>0,
解得m>;
(2)当m=1时,方程为x2﹣2x=0,
解得x1=0,x2=2.
【注:答案不唯一】
23.如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
【分析】(1)分别作出三个顶点关于原点的对称点,再首尾顺次连接即可;
(2)分别作出点A、B位似变换后的对应点,再首尾顺次连接即可.
解:(1)如图所示,△A1OB1即为所求;
(2)如图所示,△A2OB2即为所求.
24.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=18,AD=9,AF=6,求AE的长.
【分析】(1)根据四边形ABCD是平行四边形,可得AD∥BC,证明∠ADF=∠CED,∠AFD=∠C.即可得到△ADF∽△DEC;
(2)根据△ADF∽△DEC,可得=,根据AB=18,AD=9,AF=6,得到DE的长,再根据勾股定理即可求出AE的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CED,∠B+∠C=180°,
∵∠AFD+∠AFE=180°,∠AFE=∠B.
∴∠AFD=∠C.
∴△ADF∽△DEC;
(2)解:∵△ADF∽△DEC,
∴=,
∵AB=18,AD=9,AF=6,
∴=,
∴DE=27,
∵AD∥BC,AE⊥BC,
∴AE⊥AD,
在Rt△ADE中,根据勾股定理,得
AE===18.
25.如图,点E,F在正方形ABCD的对角线AC上,∠EBF=45°.
(1)当BE=BF时,求证:AE=CF;
(2)若AB=4,求AF?CE的值;
(3)延长BF交CD于点G,连接EG.判断线段BE与EG的数量关系,并说明理由.
【分析】(1)根据正方形的性质及全等三角形的性质可得结论;
(2)直接根据相似三角形的判定与性质可得答案;
(3)根据相似三角形的判定得△BEF∽△CGF.然后由相似三角形的性质得∠EBF=∠EGF.最后由等角对等边可得结论.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠BAE=∠BCF=45°,
∵BE=BF,
∴∠BEF=∠BFE.
∴∠AEB=∠CFB.
∴△ABE≌△CBF(AAS).
∴AE=CF.
(2)∵∠BEC=∠BAE+∠ABE=45°+∠ABE,
∠ABF=∠EBF+∠ABE=45°+∠ABE,
∴∠BEC=∠ABF.
∵∠BAF=∠BCE=45°,
∴△ABF∽△CEB.
∴.
∴AF?CE=AB?BC=4×4=16.
(3)解法一:EB=EG.理由如下:
如图:
∠EBF=∠GCF=45°,
∠EFB=∠GFC,
∴△BEF∽△CGF.
∴.
即.
∵∠EFG=∠BFC,
∴△EFG∽△BFC.
∴∠EGF=∠BCF=45°.
∴∠EBF=∠EGF.
∴EB=EG.
解法二:EB=EG.理由如下:
如图3,过点E作HK⊥CD交CD于点K,交AB于点H,连接BD,
∵四边形ABCD是正方形,
∴∠BAE=∠BDG=∠ABD=45°.
∴∠ABD=∠EBF=45°.
∴∠ABE=∠DBG.
∴△ABE∽△DBG.
∴.
∴.
在Rt△AHE中,∠HAE=∠AEH=45°,
∴,AH=HE.
∴.
在四边形AHKD中,
∵∠DAH=∠ADK=∠AHK=90°,
∴四边形AHKD是矩形.
∴DK=AH.
∴KG=DG﹣DK=2AH﹣AH=AH.
∴HE=KG.
在Rt△CEK中,∠KEC=∠KCE=45°,
∴EK=CK.
∵DK=AH,
∴AB﹣DK=CD﹣AH.
∴CK=BH.
∴EK=BH.
∵HE=KG,∠BHE=∠EKC=90°,EK=BH,
∴△BHE≌△EKG.
∴BE=EG.
26.在矩形ABCD中,AB=3,AD=5,E是射线DC上的点,连接AE,将△ADE沿直线AE翻折得△AFE.
(1)如图①,点F恰好在BC上,求证:△ABF∽△FCE:
(2)如图②,点F在矩形ABCD内,连接CF,若DE=1,求△EFC的面积;
(3)若以点E,F,C为顶点的三角形是直角三角形,请直接写出DE的长.
【分析】(1)先利用同角的余角相等,判断出∠CEF=∠AFB,即可得出结论;
(2)先判断出△FGE∽△AHF,得出,进而得出AH=5GF,在Rt△AHF中,根据勾股定理求出GF=,即可得出结论;
(3)分点E在线段CD上和DC的延长线上,再分别分两种情况,利用勾股定理直接计算或建立方程求解即可得出结论.
【解答】(1)解:在矩形ABCD中,∠B=∠C=∠D=90°,
由折叠可得:∠D=∠EFA=90°,
∵∠EFA=∠C=90°,
∴∠CEF+∠CFE=∠CFE+∠AFB=90°,
∴∠CEF=∠AFB,
在△ABF和△FCE中
∵∠AFB=∠CEF,∠B=∠C=90°,
∴△ABF∽△FCE;
(2)解:如图1,
过点F作FG⊥DC交DC于点G,FH⊥AB于点H,则∠EGF=∠AHF=90°
在矩形ABCD中,∠D=90°,
由折叠可得:∠D=∠EFA=90°,DE=EF=1,AD=AF=5
∵∠EGF=∠EFA=90°,
∴∠GEF+∠GFE=∠AFH+∠GFE=90°,
∴∠GEF=∠AFH,
在△FGE和△AHF中,
∵∠GEF=∠AFH,∠EGF=∠FHA=90°,
∴△FGE∽△AHF,
∴,
∴,
∴AH=5GF,
在Rt△AHF中,∠AHF=90°,
∵AH2+FH2=AF2,
∴(5GF)2+(5﹣GF)2=52,
∴GF=,
∴△EFC的面积为×2=;
(3)解:设DE=x,
∵以点E、F、C为顶点的三角形是直角三角形,
∴①当点E在线段CD上时,∠DAE<45°,
∴∠AED>45°,由折叠知,∠AEF=∠AED>45°,
∴∠DEF=∠AED+∠AEF>90°,
∴∠CEF<90°,
∴只有∠EFC=90°或∠ECF=90°,
Ⅰ、当∠EFC=90°时,如图2,
由折叠知,∠AFE=∠D=90°,
∴∠AFE+∠EFC=90°,
∴点A,F,C在同一条线上,
即:点F在矩形的对角线AC上,
在Rt△ACD中,AD=5,CD=AB=3,
根据勾股定理得,AC=,
由折叠知,EF=DE=x,AF=AD=5,
∴CF=AC﹣AF=﹣5,
在Rt△ECF中,EF2+CF2=CE2,
∴x2+(﹣5)2=(3﹣x)2,
∴x=,
即:DE=;
Ⅱ、当∠ECF=90°时,如图3,点F在BC上,由折叠知,EF=DE=x,AF=AD=5,
在Rt△ABF中,根据勾股定理得,BF==4,
∴CF=BC﹣BF=1,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
∴(3﹣x)2+12=x2,
∴x=,
即:DE=;
②当点E在DC延长线上时,CF在∠AFE内部,而∠AFE=90°,
∴∠CFE<90°,
∴只有∠CEF=90°或∠ECF=90°,
Ⅰ、当∠CEF=90°时,如图4,
由折叠知,AD=AF=5,∠AFE=90°=∠D=∠CEF,
∴四边形AFED是正方形,
∴DE=AF=5;
Ⅱ、当∠DCF=90°时,如图5,
∵∠ABC=∠BCD=90°,
∴点F在CB的延长线上,
∴∠ABF=90°,
由折叠知,EF=DE=x,AF=AD=5,
在Rt△ABF中,根据勾股定理得,BF==4,
∴CF=BC+BF=9,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
∴(x﹣3)2+92=x2,
∴x=15,
即:DE=15,
综上所述,DE的长为或或5或15,
故答案为或或5或15.
一、选择题(每小题4分,共48分).
1.下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.式子在实数范围内有意义,则x的取值范围是( )
A.x<3 B.x≥3 C.x≤3 D.x>3
3.下列各式中,运算正确的是( )
A. B. C. D.
4.如果3x=4y(y≠0),那么下列比例式中正确的是( )
A. B. C. D.
5.用配方法解方程x2﹣4x﹣1=0,方程应变形为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.(x﹣2)2=5
6.关于x的一元二次方程(k+1)x2+2x=0有两个不相等的实数根,则k的取值范围为( )
A.k>﹣1 B.k<﹣1 C.k≠﹣1 D.k<0且k≠﹣1
7.如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法判断
8.如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
9.如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是( )
A.点O B.点P C.点M D.点N
10.在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,BD=2,则CD的长为( )
A.2 B.3 C. D.
11.如图,在平行四边形ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,则图中阴影部分图形的面积之和与平行四边形ABCD的面积之比为( )
A. B. C. D.
12.平面直角坐标系中,直线y=﹣x+2和x轴,y轴分别交于A,B两点,在第二象限内有一点P,使△PAO和△AOB相似,则符合要求的点P的个数为( )
A.2 B.3 C.4 D.5
二、填空题:请将最终结果填入题中的横线上.(每小题4分,共24分)
13.如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则DF的长度为 .
14.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 .
15.已知,则的值为 .
16.设x1、x2是方程x2﹣5x+m=0的两个根,且x1+x2﹣x1x2=2,则m= .
17.如图,点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为3,4,H为线段DF的中点,则BH= .
18.如图,等边三角形ABC的边长为5,D,E分别是边AB,AC上的点,将△ADE沿DE折叠,点A恰好落在BC边上的点F处,若BF=2,则BD的长是 .
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共78分)
19.已知a=+1,求代数式a2﹣2a+7的值.
20.解方程:(x﹣7)2﹣3x(7﹣x)=0.
21.如图,在△ABC中,点D,E分别在边AB,AC上,连接DE,且AD?AB=AE?AC.
(1)求证:△ADE∽△ACB;
(2)若∠B=55°,∠ADE=75°,求∠A的度数.
22.关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
23.如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
24.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=18,AD=9,AF=6,求AE的长.
25.如图,点E,F在正方形ABCD的对角线AC上,∠EBF=45°.
(1)当BE=BF时,求证:AE=CF;
(2)若AB=4,求AF?CE的值;
(3)延长BF交CD于点G,连接EG.判断线段BE与EG的数量关系,并说明理由.
26.在矩形ABCD中,AB=3,AD=5,E是射线DC上的点,连接AE,将△ADE沿直线AE翻折得△AFE.
(1)如图①,点F恰好在BC上,求证:△ABF∽△FCE:
(2)如图②,点F在矩形ABCD内,连接CF,若DE=1,求△EFC的面积;
(3)若以点E,F,C为顶点的三角形是直角三角形,请直接写出DE的长.
参考答案
一、选择题(在每小题给出的四个选项中,只有一个是正确的,请把正确的选项填在题后的括号内,每小题4分,共48分)
1.下列图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形以及轴对称图形的概念对各选项分析判断即可.
解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.不是轴对称图形,是中心对称图形,故本选项不合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.是轴对称图形,不是中心对称图形,故本选项不合题意.
故选:A.
2.式子在实数范围内有意义,则x的取值范围是( )
A.x<3 B.x≥3 C.x≤3 D.x>3
【分析】直接利用二次根式有意义的条件分析得出答案.
解:式子在实数范围内有意义,故x﹣3≥0,
则x的取值范围是:x≥3.
故选:B.
3.下列各式中,运算正确的是( )
A. B. C. D.
【分析】直接利用二次根式的性质分别化简计算得出答案.
解:A、=2,正确;
B、3﹣=2,故此选项错误;
C、2+,无法计算,故此选项错误;
D、=2,故此选项错误.
故选:A.
4.如果3x=4y(y≠0),那么下列比例式中正确的是( )
A. B. C. D.
【分析】根据比例的性质,可得答案.
解:A、由比例的性质,得4x=3y与3x=4y不一致,故A不符合题意;
B、由比例的性质,得xy=12与3x=4y不一致,故B不符合题意;
C、由比例的性质,得4x=3y与3x=4y不一致,故C不符合题意;
D、由比例的性质,得3x=4y与3x=4y一致,故D符合题意;
故选:D.
5.用配方法解方程x2﹣4x﹣1=0,方程应变形为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.(x﹣2)2=5
【分析】常数项移到方程的右边后,两边配上一次项系数一半的平方,写成完全平方式即可得.
解:∵x2﹣4x=1,
∴x2﹣4x+4=1+4,即(x﹣2)2=5,
故选:D.
6.关于x的一元二次方程(k+1)x2+2x=0有两个不相等的实数根,则k的取值范围为( )
A.k>﹣1 B.k<﹣1 C.k≠﹣1 D.k<0且k≠﹣1
【分析】根据根的判别式和一元二方程的定义得出△=22﹣4(k+1)×0>0且k+1≠0,求出即可.
解:∵关于x的一元二次方程(k+1)x2+2x=0有两个不相等的实数根,
∴△=22﹣4(k+1)×0>0且k+1≠0,
解得:k≠﹣1,
故选:C.
7.如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是( )
A.矩形 B.菱形 C.正方形 D.无法判断
【分析】由条件可知AB∥CD,AD∥BC,再证明AB=BC即可解决问题.
解:过点D作DE⊥AB于E,DF⊥BC于F.
∵两直尺的宽度相等,
∴DE=DF.
又∵平行四边形ABCD的面积=AB?DE=BC?DF,
∴AB=BC,
∴平行四边形ABCD为菱形.
故选:B.
8.如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
【分析】根据相似三角形的判定定理对各选项进行逐一判定即可.
解:A、根据平行线截得的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
C、两三角形的对应角不一定相等,故两三角形不相似,故本选项符合题意;
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项不符合题意.
故选:C.
9.如图所示,在边长为1的小正方形网格中,两个三角形是位似图形,则它们的位似中心是( )
A.点O B.点P C.点M D.点N
【分析】直接利用位似图形的性质进而连接对应点得出位似中心即可.
解:如图所示:两个三角形的位似中心是:点P.
故选:B.
10.在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,BD=2,则CD的长为( )
A.2 B.3 C. D.
【分析】证明△BDA∽△ADC,根据相似三角形的性质列出比例式,把已知数据代入计算,得到答案.
解:∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵AD⊥BC,
∴∠C+∠CAD=90°,
∴∠C=∠BAD,
∵∠BDA=∠ADC=90°,
∴△BDA∽△ADC,
∴,
即,
解得,DC=,
故选:D.
11.如图,在平行四边形ABCD中,E,F分别是边BC,CD的中点,AE,AF分别交BD于点G,H,则图中阴影部分图形的面积之和与平行四边形ABCD的面积之比为( )
A. B. C. D.
【分析】依据相似三角形的对应边成比例,即可得到GH=BD,进而得出S△AGH=S△ABD=S四边形ABCD;依据三角形中位线定理,即可得到S△CEF=S△BCD=S四边形ABCD,据此可得阴影部分图形的面积与?ABCD的面积之比.
解:∵BE∥AD,E是BC的中点,
∴△BEG∽△DAG,
∴,即BG=BD,
同理可得,DH=BD,
∴GH=BD,
∴S△AGH=S△ABD=S四边形ABCD,
∵E、F分别是边BC、CD的中点,
∴EF∥BD,EF=BD,
∴△CEF∽△CBD,
∴,
∴S△CEF=S△BCD=S四边形ABCD,,
∴图中阴影部分图形的面积=()S四边形ABCD=S四边形ABCD,
即图中阴影部分图形的面积与?ABCD的面积之比为=7:24,
故选:B.
12.平面直角坐标系中,直线y=﹣x+2和x轴,y轴分别交于A,B两点,在第二象限内有一点P,使△PAO和△AOB相似,则符合要求的点P的个数为( )
A.2 B.3 C.4 D.5
【分析】根据相似三角形的相似条件,画出图形即可解决问题.
解:如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选:C.
二、填空题:请将最终结果填入题中的横线上.(每小题4分,共24分)
13.如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则DF的长度为 4 .
【分析】先求出AB=BC,根据平行线分线段成比例定理得出比例式,代入即可求出EF,再求出DF即可.
解:∵点B是线段AC的中点,
∴AB=BC,
∴=1,
∵直线a∥b∥c,
∴==1,
∵DE=2,
∴EF=2,
∴DF=DE+EF=2+2=4,
故答案为:4.
14.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 8 .
【分析】根据线段比例中项的概念a:c=c:b,可得c2=ab=64,即可求出c的值.
解:∵线段c是a、b的比例中项,
∴c2=ab=64,
解得:c=±8,
又∵线段是正数,
∴c=8.
故答案为:8.
15.已知,则的值为 .
【分析】直接利用已知将原式变形进而得出答案.
解:∵,
∴3a﹣3b=2b,
故3a=5b,
∴的值为:.
故答案为:.
16.设x1、x2是方程x2﹣5x+m=0的两个根,且x1+x2﹣x1x2=2,则m= 3 .
【分析】由根与系数的关系可得x1+x2=5、x1x2=m,结合x1+x2﹣x1x2=2可得出关于m的一元一次方程,解之即可得出结论.
解:∵x1、x2是方程x2﹣5x+m=0的两个根,
∴x1+x2=5,x1x2=m.
∵x1+x2﹣x1x2=5﹣m=2,
∴m=3.
故答案为:3.
17.如图,点A,B,E在同一条直线上,正方形ABCD,BEFG的边长分别为3,4,H为线段DF的中点,则BH= .
【分析】作辅助线,连接BD,BF,可得三角形DBF为直角三角形,求出DF,根据直角三角形斜边中线可得结论.
解:连接BD、BF,
∵四边形ABCD,BEFG是正方形,且边长分别为3和4,
∴∠DBC=∠GBF=45°,BD=3,BF=4,
∴∠DBF=90°,
由勾股定理得:DF==5,
∵H为线段DF的中点,
∴BH=DF=.
故答案为:.
18.如图,等边三角形ABC的边长为5,D,E分别是边AB,AC上的点,将△ADE沿DE折叠,点A恰好落在BC边上的点F处,若BF=2,则BD的长是 .
【分析】根据翻转变换的性质可知,DA=DF,EA=EF,∠DFE=∠A=60°,利用相似三角形△DBF∽△FCE,对应边成比例,列方程求解即可.
解:∵等边三角形ABC的边长为5,BF=2,
∴FC=5﹣2=3,AB=BC=AC=5,∠A=∠B=∠C=60°,
由翻转变换的性质可知,DA=DF,EA=EF,∠DFE=∠A=60°,
∵∠DFC=∠BDF+∠B,即∠DFE+∠EFC=∠BDF+∠B,
∴∠BDF=∠CFE,
又∵∠B=∠C=60°,
∴△DBF∽△FCE,
∴==,
设BD=x,则AD=5﹣x=DF,
即==,
∴EC=,FE=,
又∵EC+EF=EC+EA=AC=5,
∴+=5,
解得x=,
经检验x=是方程的解,
∴BD=,
故答案为:.
三、解答题.解答要写出必要的文字说明、证明过程或演算步骤(共78分)
19.已知a=+1,求代数式a2﹣2a+7的值.
【分析】将a的值代入a2﹣2a+7=(a﹣1)2+6计算可得.
解:a2﹣2a+7=(a﹣1)2+6,
当时,
原式=(+1﹣1)2+6
=5+6
=11.
20.解方程:(x﹣7)2﹣3x(7﹣x)=0.
【分析】将方程左边多项式第二项提取﹣1变形后,提取公因式x﹣7化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解:方程变形得:(x﹣7)2+3x(x﹣7)=0,
分解因式得:(x﹣7)(x﹣7+3x)=0,即(x﹣7)(4x﹣7)=0,
可得x﹣7=0或4x﹣7=0,
∴x1=7,x2=.
21.如图,在△ABC中,点D,E分别在边AB,AC上,连接DE,且AD?AB=AE?AC.
(1)求证:△ADE∽△ACB;
(2)若∠B=55°,∠ADE=75°,求∠A的度数.
【分析】(1)本题根据相似三角形的判定可以推出△ADE∽△ACB.
(2)由第(1)问可知△ADE∽△ACB,进而得到∠ADE=∠ACB,从而得到∠ACB=75°,在利用三角形的内角和得出所求角即可.
【解答】(1)证明:
∵AD?AB=AE?AC,
∴.
又∵∠A=∠A,
∴△ADE∽△ACB.
(2)解:由(1)知,△ADE∽△ACB,
∴∠ADE=∠ACB.
∵∠ADE=75°,
∴∠ACB=75°.
又∵∠B=55°,
∴∠A=180°﹣∠ACB﹣∠B=50°.
22.关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
【分析】(1)由方程根的情况,根据根的判别式可得到关于m的方程,则可求得m的取值范围;
(2)由(1)中所求m的取值范围,取一个m的值,代入方程求解即可.
解:(1)∵关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个不相等的实数根,
∴△>0,即(﹣2m)2﹣4(m﹣1)2=8m﹣4>0,
解得m>;
(2)当m=1时,方程为x2﹣2x=0,
解得x1=0,x2=2.
【注:答案不唯一】
23.如图,在直角坐标系xOy中,△AOB的顶点坐标分别是A(1,0),O(0,0),B(2,2).
(1)画出△A1OB1,使△A1OB1与△AOB关于点O中心对称;
(2)以点O为位似中心将△AOB放大,得到△A2OB2,使△A2OB2与△AOB的相似比为2:1,画出一个满足条件的△A2OB2.
【分析】(1)分别作出三个顶点关于原点的对称点,再首尾顺次连接即可;
(2)分别作出点A、B位似变换后的对应点,再首尾顺次连接即可.
解:(1)如图所示,△A1OB1即为所求;
(2)如图所示,△A2OB2即为所求.
24.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=18,AD=9,AF=6,求AE的长.
【分析】(1)根据四边形ABCD是平行四边形,可得AD∥BC,证明∠ADF=∠CED,∠AFD=∠C.即可得到△ADF∽△DEC;
(2)根据△ADF∽△DEC,可得=,根据AB=18,AD=9,AF=6,得到DE的长,再根据勾股定理即可求出AE的长.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠CED,∠B+∠C=180°,
∵∠AFD+∠AFE=180°,∠AFE=∠B.
∴∠AFD=∠C.
∴△ADF∽△DEC;
(2)解:∵△ADF∽△DEC,
∴=,
∵AB=18,AD=9,AF=6,
∴=,
∴DE=27,
∵AD∥BC,AE⊥BC,
∴AE⊥AD,
在Rt△ADE中,根据勾股定理,得
AE===18.
25.如图,点E,F在正方形ABCD的对角线AC上,∠EBF=45°.
(1)当BE=BF时,求证:AE=CF;
(2)若AB=4,求AF?CE的值;
(3)延长BF交CD于点G,连接EG.判断线段BE与EG的数量关系,并说明理由.
【分析】(1)根据正方形的性质及全等三角形的性质可得结论;
(2)直接根据相似三角形的判定与性质可得答案;
(3)根据相似三角形的判定得△BEF∽△CGF.然后由相似三角形的性质得∠EBF=∠EGF.最后由等角对等边可得结论.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠BAE=∠BCF=45°,
∵BE=BF,
∴∠BEF=∠BFE.
∴∠AEB=∠CFB.
∴△ABE≌△CBF(AAS).
∴AE=CF.
(2)∵∠BEC=∠BAE+∠ABE=45°+∠ABE,
∠ABF=∠EBF+∠ABE=45°+∠ABE,
∴∠BEC=∠ABF.
∵∠BAF=∠BCE=45°,
∴△ABF∽△CEB.
∴.
∴AF?CE=AB?BC=4×4=16.
(3)解法一:EB=EG.理由如下:
如图:
∠EBF=∠GCF=45°,
∠EFB=∠GFC,
∴△BEF∽△CGF.
∴.
即.
∵∠EFG=∠BFC,
∴△EFG∽△BFC.
∴∠EGF=∠BCF=45°.
∴∠EBF=∠EGF.
∴EB=EG.
解法二:EB=EG.理由如下:
如图3,过点E作HK⊥CD交CD于点K,交AB于点H,连接BD,
∵四边形ABCD是正方形,
∴∠BAE=∠BDG=∠ABD=45°.
∴∠ABD=∠EBF=45°.
∴∠ABE=∠DBG.
∴△ABE∽△DBG.
∴.
∴.
在Rt△AHE中,∠HAE=∠AEH=45°,
∴,AH=HE.
∴.
在四边形AHKD中,
∵∠DAH=∠ADK=∠AHK=90°,
∴四边形AHKD是矩形.
∴DK=AH.
∴KG=DG﹣DK=2AH﹣AH=AH.
∴HE=KG.
在Rt△CEK中,∠KEC=∠KCE=45°,
∴EK=CK.
∵DK=AH,
∴AB﹣DK=CD﹣AH.
∴CK=BH.
∴EK=BH.
∵HE=KG,∠BHE=∠EKC=90°,EK=BH,
∴△BHE≌△EKG.
∴BE=EG.
26.在矩形ABCD中,AB=3,AD=5,E是射线DC上的点,连接AE,将△ADE沿直线AE翻折得△AFE.
(1)如图①,点F恰好在BC上,求证:△ABF∽△FCE:
(2)如图②,点F在矩形ABCD内,连接CF,若DE=1,求△EFC的面积;
(3)若以点E,F,C为顶点的三角形是直角三角形,请直接写出DE的长.
【分析】(1)先利用同角的余角相等,判断出∠CEF=∠AFB,即可得出结论;
(2)先判断出△FGE∽△AHF,得出,进而得出AH=5GF,在Rt△AHF中,根据勾股定理求出GF=,即可得出结论;
(3)分点E在线段CD上和DC的延长线上,再分别分两种情况,利用勾股定理直接计算或建立方程求解即可得出结论.
【解答】(1)解:在矩形ABCD中,∠B=∠C=∠D=90°,
由折叠可得:∠D=∠EFA=90°,
∵∠EFA=∠C=90°,
∴∠CEF+∠CFE=∠CFE+∠AFB=90°,
∴∠CEF=∠AFB,
在△ABF和△FCE中
∵∠AFB=∠CEF,∠B=∠C=90°,
∴△ABF∽△FCE;
(2)解:如图1,
过点F作FG⊥DC交DC于点G,FH⊥AB于点H,则∠EGF=∠AHF=90°
在矩形ABCD中,∠D=90°,
由折叠可得:∠D=∠EFA=90°,DE=EF=1,AD=AF=5
∵∠EGF=∠EFA=90°,
∴∠GEF+∠GFE=∠AFH+∠GFE=90°,
∴∠GEF=∠AFH,
在△FGE和△AHF中,
∵∠GEF=∠AFH,∠EGF=∠FHA=90°,
∴△FGE∽△AHF,
∴,
∴,
∴AH=5GF,
在Rt△AHF中,∠AHF=90°,
∵AH2+FH2=AF2,
∴(5GF)2+(5﹣GF)2=52,
∴GF=,
∴△EFC的面积为×2=;
(3)解:设DE=x,
∵以点E、F、C为顶点的三角形是直角三角形,
∴①当点E在线段CD上时,∠DAE<45°,
∴∠AED>45°,由折叠知,∠AEF=∠AED>45°,
∴∠DEF=∠AED+∠AEF>90°,
∴∠CEF<90°,
∴只有∠EFC=90°或∠ECF=90°,
Ⅰ、当∠EFC=90°时,如图2,
由折叠知,∠AFE=∠D=90°,
∴∠AFE+∠EFC=90°,
∴点A,F,C在同一条线上,
即:点F在矩形的对角线AC上,
在Rt△ACD中,AD=5,CD=AB=3,
根据勾股定理得,AC=,
由折叠知,EF=DE=x,AF=AD=5,
∴CF=AC﹣AF=﹣5,
在Rt△ECF中,EF2+CF2=CE2,
∴x2+(﹣5)2=(3﹣x)2,
∴x=,
即:DE=;
Ⅱ、当∠ECF=90°时,如图3,点F在BC上,由折叠知,EF=DE=x,AF=AD=5,
在Rt△ABF中,根据勾股定理得,BF==4,
∴CF=BC﹣BF=1,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
∴(3﹣x)2+12=x2,
∴x=,
即:DE=;
②当点E在DC延长线上时,CF在∠AFE内部,而∠AFE=90°,
∴∠CFE<90°,
∴只有∠CEF=90°或∠ECF=90°,
Ⅰ、当∠CEF=90°时,如图4,
由折叠知,AD=AF=5,∠AFE=90°=∠D=∠CEF,
∴四边形AFED是正方形,
∴DE=AF=5;
Ⅱ、当∠DCF=90°时,如图5,
∵∠ABC=∠BCD=90°,
∴点F在CB的延长线上,
∴∠ABF=90°,
由折叠知,EF=DE=x,AF=AD=5,
在Rt△ABF中,根据勾股定理得,BF==4,
∴CF=BC+BF=9,
在Rt△ECF中,根据勾股定理得,CE2+CF2=EF2,
∴(x﹣3)2+92=x2,
∴x=15,
即:DE=15,
综上所述,DE的长为或或5或15,
故答案为或或5或15.
同课章节目录
