全等三角形
图片预览






文档简介
(共27张PPT)
全等三角形
能够完全重合的两个图形叫做全等形
A
B
C
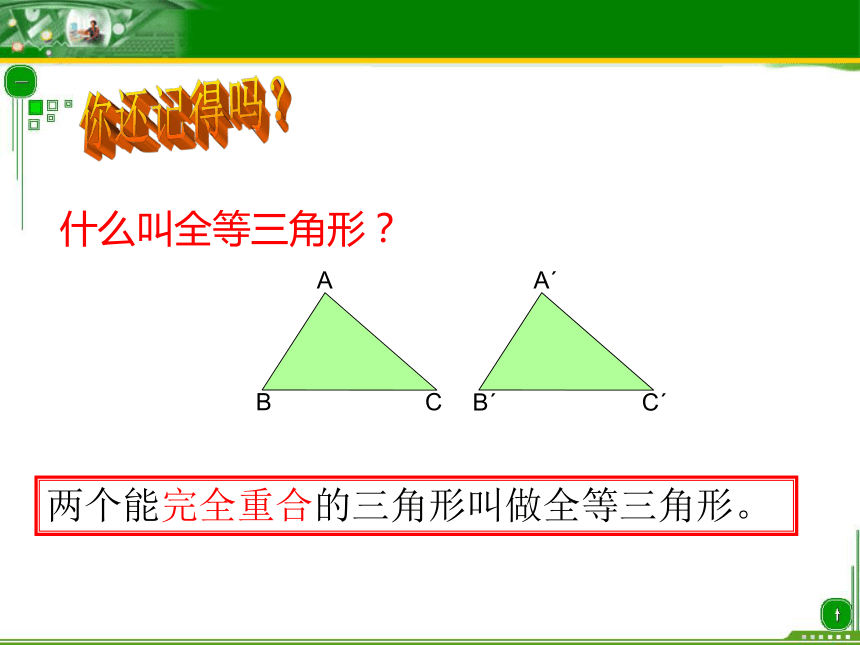
什么叫全等三角形?
两个能完全重合的三角形叫做全等三角形。
Aˊ
Bˊ
Cˊ
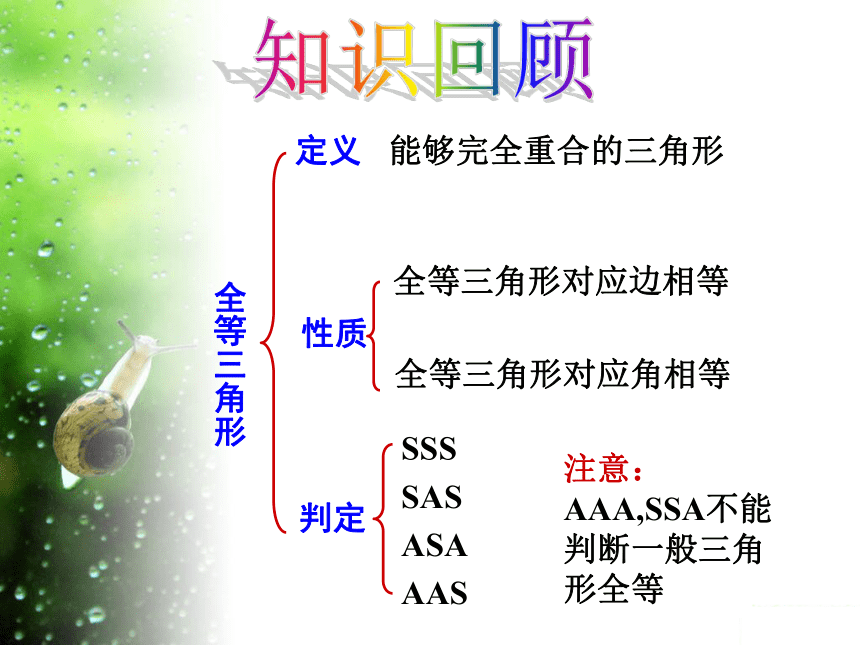
全等三角形
定义
能够完全重合的三角形
性质
全等三角形对应边相等
全等三角形对应角相等
判定
SSS
SAS
ASA
AAS
注意:AAA,SSA不能判断一般三角形全等
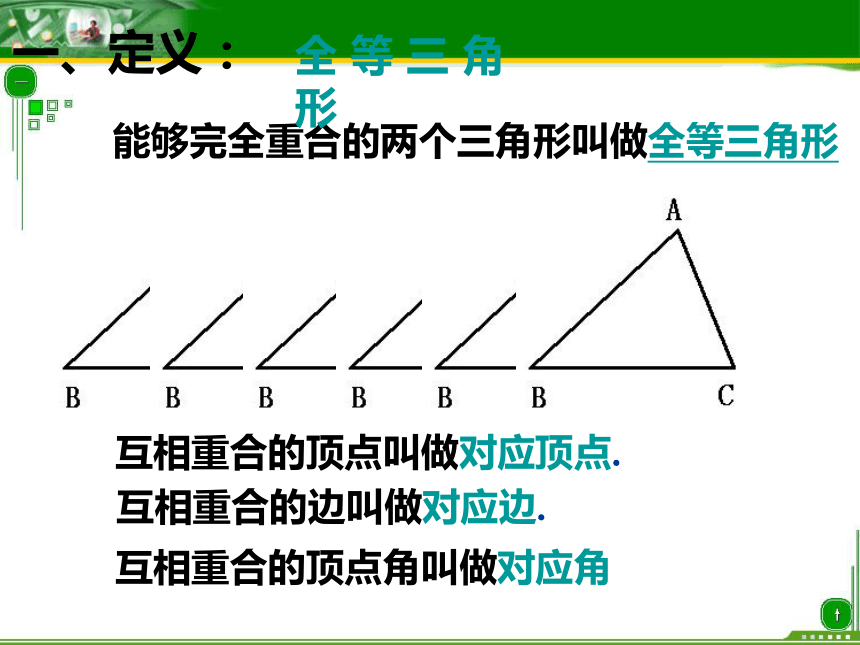
一、定义:
能够完全重合的两个三角形叫做全等三角形
互相重合的顶点叫做对应顶点.
互相重合的边叫做对应边.
互相重合的顶点角叫做对应角
全 等 三 角 形
1.全等三角形的性质:
对应边、对应角、对应线段相等,周长、面积也相等。
2.全等三角形的判定:
知识点
①一般三角形全等的判定:
SAS、ASA、AAS、SSS
②直角三角形全等的判定:
SAS、ASA、AAS、SSS、HL
知识点
3.三角形全等的证题思路:
①
②
③
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
请填空
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
二、全等三角形的性质
(全等三角形的对应边相等)
(全等三角形的对应角相等)
全等三角形的对应边相等,对应角相等。
∵△ABC≌ △A’B’C’
∴ AB=A’B’, BC=B’C’, AC=A’C’
∴ ∠ A= ∠ A’, ∠ B= ∠B’ ,
∠ C= ∠C’
*
6.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
解:∵AE=CF(已知)
A
D
B
C
F
E
∴AE-FE=CF-EF(等量减等量,差相等)
即AF=CE
在△AFD和△CEB中,
∴△AFD≌△CEB
∠AFD=∠CEB(已知)
DF=BE(已知)
AF=CE(已证)
(SAS)
*
7.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
A
C
E
B
D
解:∵ ∠CAE=∠BAD(已知)
∴ ∠CAE+∠BAE=∠BAD+∠BAE
(等量减等量,差相等)
即∠BAC=∠DAE
在△ABC和△ADE中,
∴△ABC≌ △ADE
∠BAC=∠DAE(已证)
AC=AE(已知)
∠B=∠D(已知)
(AAS)
*
8.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。
解: 连接AC
∴△ADC≌△ABC(SSS)
∴ ∠ABC=∠ADC
(全等三角形的对应角相等)
在△ABC和△ADC中,
BC=DC(已知)
AC=AC(公共边)
AB=AD(已知)
*
11. 如图,M是AB的中点 ,∠1 = 2 ,MC=MD.试说明ΔACM ≌ ΔBDM
A
B
M
C
D
(
)
1
2
证明: ∵ M是AB的中点 (已知)
∴ MA=MB(中点定义)
在ΔACM 和ΔBDM中,
MA=MB(已证)
∠1 = ∠2 (已知)
MC=MD(已知)
∴ΔACM ≌ ΔBDM (SAS)
1.请指出图中全等三角形的对应边和对应角
如右图中△ ABD ≌ △CDB,
则AB= ;AD= ;BD= ; ∠ABD=__ ; ∠ADB=______ ; ∠A=__ ;
随堂练习
CD
CB
BD
∠CDB
∠CBD
∠C
AB与CD、AD与CB、BD与DB
∠ABD与∠CDB、
∠ADB与∠CBD、∠A与∠C
3、如图△ ABD ≌ △CDB,
若AB=4,AD=5,BD=6,则BC= ,CD=______,
达标测试
5
4
4、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
达标测试
解:
∵△ABD≌ △EBC
∴AB=EB、BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm
达标测试
1、能够 的两个图形叫做全等形.
两个三角形重合时,互相 _的顶点
叫做对应顶点.记两个全等三角形时,
通常把表示 _顶点的字母写在____
的位置上.
A
B
C
D
E
2、如图△ABC≌ △ADE
若∠D=∠B, ∠C= ∠AED,
则∠DAE= ; ∠DAB= 。
重合
重合
重合
相对应
∠BAC
∠EAC
例题选析
例1:如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一具条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B. ∠AEB=∠ADC
C.BE=CD D.AB=AC
B
例2:已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对
D
例3:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A=∠ C(全等三角形的对应角相等)
你能说明AB∥CD,AD∥BC吗?
1.如图,在△ABC中,AB=AC, ∠BAC=90 °
D是BC上一点,EC⊥BC.EC=BD,
试证明AD=AE.
证明;在△ABC中,AB=AC, ∠BAC=90 °
∴△ ABC是等腰直角三角形.
∴∠ ABC=∠ACB=45 °又∵ EC⊥BC
∴∠ ACE=90 °- ∠ACB=45 °
∴ ∠ ACE= ∠ ABC =45 °
∵ AB=AC , ∠ ACE= ∠ ABC ,
EC=BD
∴ △ABD≌△ACE ∴ AD=AE
2.如图所示,已知CA⊥ AB,DB⊥AB,AC=BE,CE ⊥ ED.试猜想线段CE与DE的大小与位置关系,并说明理由.
证明:∵已知CA⊥ AB,DB⊥AB
∴∠A=∠B=90 °, ∠C+ ∠CED=90°
又∵ CE ⊥ ED, ∴ ∠DEB+ ∠CED=90°
∠C = ∠DEB
又∵ ∠A=∠B ,AC=BE
∴ △CAE= △EBD
∴ CE =DE
3.如图所示,已知△ABE和△ACD是等边三角形,求证:EC=BD.
证明: ∵ △ABE和△ACD是等边三角形
∴AB=AE, AC= AD, ∠EAB=∠DAC=60°
∴ ∠EAB+ ∠BAC =∠DAC + ∠BAC
∴ ∠EAC= ∠DAB
∴ AB=AE
∠EAC= ∠DAB
AC= AD
∴△EAC≌△BAD
∴ EC=BD
谢谢,再见!
欧
全等三角形
能够完全重合的两个图形叫做全等形
A
B
C
什么叫全等三角形?
两个能完全重合的三角形叫做全等三角形。
Aˊ
Bˊ
Cˊ
全等三角形
定义
能够完全重合的三角形
性质
全等三角形对应边相等
全等三角形对应角相等
判定
SSS
SAS
ASA
AAS
注意:AAA,SSA不能判断一般三角形全等
一、定义:
能够完全重合的两个三角形叫做全等三角形
互相重合的顶点叫做对应顶点.
互相重合的边叫做对应边.
互相重合的顶点角叫做对应角
全 等 三 角 形
1.全等三角形的性质:
对应边、对应角、对应线段相等,周长、面积也相等。
2.全等三角形的判定:
知识点
①一般三角形全等的判定:
SAS、ASA、AAS、SSS
②直角三角形全等的判定:
SAS、ASA、AAS、SSS、HL
知识点
3.三角形全等的证题思路:
①
②
③
1、若△AOC≌△BOD,AC=
∠A=
A
B
O
C
D
2、若△ABD≌△ACE,BD= ,
∠BDA=
3、若△ABC≌△CDA,AB=
∠BAC=
A
B
C
D
请填空
BD
∠B
CE
∠CEA
CD
∠DCA
A
B
C
D
E
公共点
公共角
公共边
二、全等三角形的性质
(全等三角形的对应边相等)
(全等三角形的对应角相等)
全等三角形的对应边相等,对应角相等。
∵△ABC≌ △A’B’C’
∴ AB=A’B’, BC=B’C’, AC=A’C’
∴ ∠ A= ∠ A’, ∠ B= ∠B’ ,
∠ C= ∠C’
*
6.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
解:∵AE=CF(已知)
A
D
B
C
F
E
∴AE-FE=CF-EF(等量减等量,差相等)
即AF=CE
在△AFD和△CEB中,
∴△AFD≌△CEB
∠AFD=∠CEB(已知)
DF=BE(已知)
AF=CE(已证)
(SAS)
*
7.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
A
C
E
B
D
解:∵ ∠CAE=∠BAD(已知)
∴ ∠CAE+∠BAE=∠BAD+∠BAE
(等量减等量,差相等)
即∠BAC=∠DAE
在△ABC和△ADE中,
∴△ABC≌ △ADE
∠BAC=∠DAE(已证)
AC=AE(已知)
∠B=∠D(已知)
(AAS)
*
8.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。
解: 连接AC
∴△ADC≌△ABC(SSS)
∴ ∠ABC=∠ADC
(全等三角形的对应角相等)
在△ABC和△ADC中,
BC=DC(已知)
AC=AC(公共边)
AB=AD(已知)
*
11. 如图,M是AB的中点 ,∠1 = 2 ,MC=MD.试说明ΔACM ≌ ΔBDM
A
B
M
C
D
(
)
1
2
证明: ∵ M是AB的中点 (已知)
∴ MA=MB(中点定义)
在ΔACM 和ΔBDM中,
MA=MB(已证)
∠1 = ∠2 (已知)
MC=MD(已知)
∴ΔACM ≌ ΔBDM (SAS)
1.请指出图中全等三角形的对应边和对应角
如右图中△ ABD ≌ △CDB,
则AB= ;AD= ;BD= ; ∠ABD=__ ; ∠ADB=______ ; ∠A=__ ;
随堂练习
CD
CB
BD
∠CDB
∠CBD
∠C
AB与CD、AD与CB、BD与DB
∠ABD与∠CDB、
∠ADB与∠CBD、∠A与∠C
3、如图△ ABD ≌ △CDB,
若AB=4,AD=5,BD=6,则BC= ,CD=______,
达标测试
5
4
4、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
达标测试
解:
∵△ABD≌ △EBC
∴AB=EB、BD=BC
∵BD=DE+EB
∴DE=BD-EB
=BC-AB
=5-3=2cm
达标测试
1、能够 的两个图形叫做全等形.
两个三角形重合时,互相 _的顶点
叫做对应顶点.记两个全等三角形时,
通常把表示 _顶点的字母写在____
的位置上.
A
B
C
D
E
2、如图△ABC≌ △ADE
若∠D=∠B, ∠C= ∠AED,
则∠DAE= ; ∠DAB= 。
重合
重合
重合
相对应
∠BAC
∠EAC
例题选析
例1:如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一具条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B. ∠AEB=∠ADC
C.BE=CD D.AB=AC
B
例2:已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对
D
例3:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A=∠ C(全等三角形的对应角相等)
你能说明AB∥CD,AD∥BC吗?
1.如图,在△ABC中,AB=AC, ∠BAC=90 °
D是BC上一点,EC⊥BC.EC=BD,
试证明AD=AE.
证明;在△ABC中,AB=AC, ∠BAC=90 °
∴△ ABC是等腰直角三角形.
∴∠ ABC=∠ACB=45 °又∵ EC⊥BC
∴∠ ACE=90 °- ∠ACB=45 °
∴ ∠ ACE= ∠ ABC =45 °
∵ AB=AC , ∠ ACE= ∠ ABC ,
EC=BD
∴ △ABD≌△ACE ∴ AD=AE
2.如图所示,已知CA⊥ AB,DB⊥AB,AC=BE,CE ⊥ ED.试猜想线段CE与DE的大小与位置关系,并说明理由.
证明:∵已知CA⊥ AB,DB⊥AB
∴∠A=∠B=90 °, ∠C+ ∠CED=90°
又∵ CE ⊥ ED, ∴ ∠DEB+ ∠CED=90°
∠C = ∠DEB
又∵ ∠A=∠B ,AC=BE
∴ △CAE= △EBD
∴ CE =DE
3.如图所示,已知△ABE和△ACD是等边三角形,求证:EC=BD.
证明: ∵ △ABE和△ACD是等边三角形
∴AB=AE, AC= AD, ∠EAB=∠DAC=60°
∴ ∠EAB+ ∠BAC =∠DAC + ∠BAC
∴ ∠EAC= ∠DAB
∴ AB=AE
∠EAC= ∠DAB
AC= AD
∴△EAC≌△BAD
∴ EC=BD
谢谢,再见!
欧
