七年级数学《平面直角坐标系》导学案
文档属性
| 名称 | 七年级数学《平面直角坐标系》导学案 | 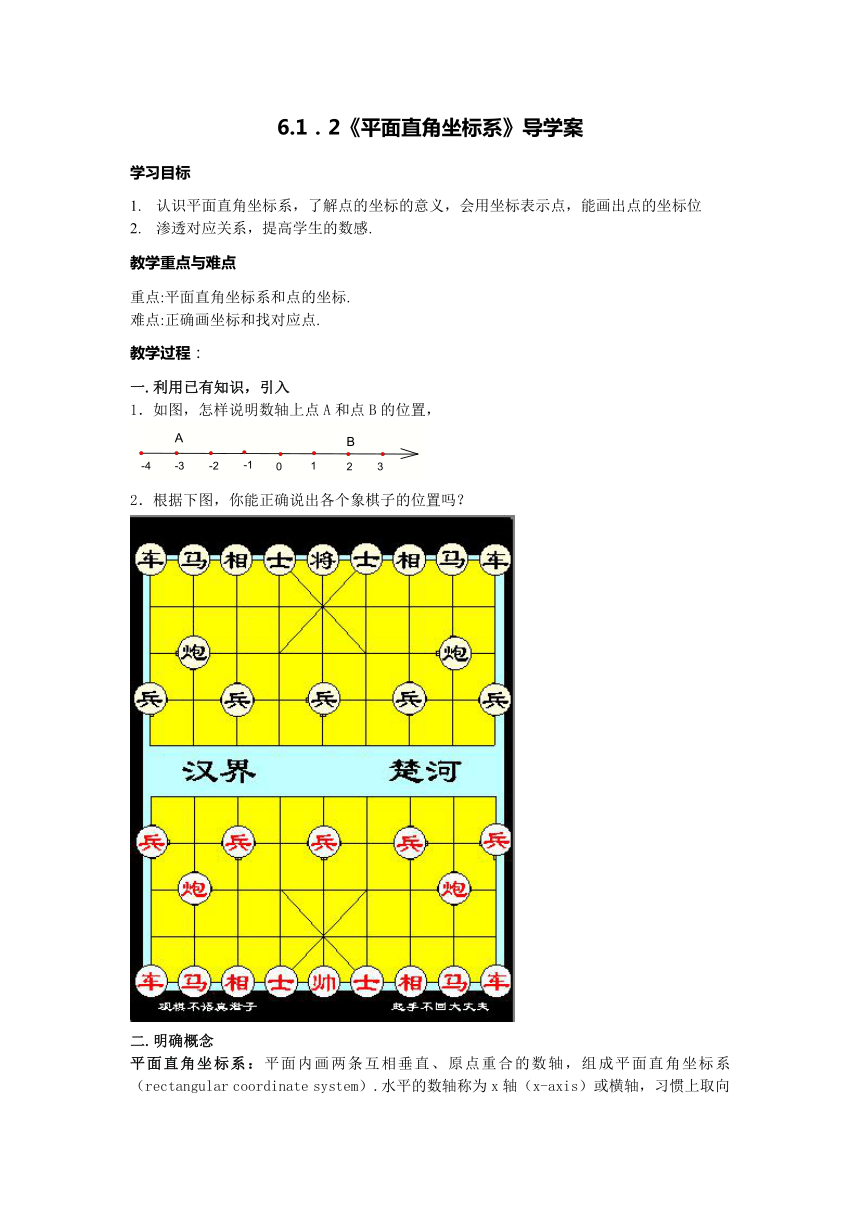 | |
| 格式 | zip | ||
| 文件大小 | 36.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-01 15:11:37 | ||
图片预览


文档简介
6.1.2《平面直角坐标系》导学案
学习目标
认识平面直角坐标系,了解点的坐标的意义,会用坐标表示点,能画出点的坐标位
渗透对应关系,提高学生的数感.
教学重点与难点
重点:平面直角坐标系和点的坐标.
难点:正确画坐标和找对应点.
教学过程:
一.利用已有知识,引入
1.如图,怎样说明数轴上点A和点B的位置,
2.根据下图,你能正确说出各个象棋子的位置吗?
二.明确概念
平面直角坐标系:平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系(rectangular coordinate system).水平的数轴称为x轴(x-axis)或横轴,习惯上取向右为正方向;竖直的数轴为y轴(y-axis)或纵轴,取向上方向为正方向;两个坐标轴的交点为平面直角坐标系的原点。
点的坐标:我们用一对有序数对表示平面上的点,这对数叫坐标。表示方法为(a,b).a是点对应横轴上的数值,b是点在纵轴上对应的数值。
例1 写出图中A、B、C、D点的坐标。
建立平面直角坐标系后,平面被坐标轴分成四部分,分别叫第一象限,第二象限,第三象限和第四象限。
你能说出例1中各点在第几象限吗?
例2 在平面直角坐标系中描出下列各点。
()A(3,4);B(-1,2);C(-3,-2);D(2,-2)
问题1:各象限点的坐标有什么特征?
练习:教材49页:练习1,2。
三.深入探索
教材48页:探索:
识别坐标和点的位置关系,以及由坐标判断两点的关系以及两点所确定的直线的位置关系。
[巩固练习]
教材49页习题6.1——第1题
教材50页——第2,4,5,6。
[小结]
平面直角坐标系;
点的坐标及其表示
各象限内点的坐标的特征
坐标轴上的点的坐标特征
平行于X轴的直线上点的坐标特征
平行于Y轴的直线上点的坐标特征
关于X轴对称的点坐标特征
关于X轴对称的点坐标特征
关于原点对称的点坐标特征
坐标的简单应用
[作业]
必做题:教科书50页:3题
(教材51页综合运用7,8,9,10为练习课内容)
6.1.2 检测题
一、选择题:
1.如图1所示,点A的坐标是 ( )毛
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
2.如图1所示,横坐标和纵坐标都是负数的点是 ( ) A.A点 B.B点 C.C点 D.D点
3.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
4.若点M的坐标是(a,b),且a>0,b<0,则点M在( )
A.第一象限;B.第二象限; C.第三象限;D.第四象限
二、填空题:
1.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.
2.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.
3.在坐标平面内,已知点A(a,b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.
4.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
5.已知点M(a,b),当a>0,b>0时,M在第_______象限;当a____,b______时,M 在第二象限;当a_____,b_______时,M在第四象限;当a<0,b<0时,M在第______象限.
三、基础训练:(共12分)
如果点A的坐标为(a2+1,-1-b2),那么点A在第几象限 为什么
四、提高训练:
如果点A(t-3s,2t+2s),B(14-2t+s,3t+2s-2)关于x轴对称,求s,t的值.
五、探索发现:
如图所示,C,D两点的横坐标分别为2,3,线段CD=1;B,D两点的横坐标分别为-2,3,线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1.
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1 (2)如果y轴上有两点P(0,y1),Q(0,y2)(y1 六、能力提高:
如果│3x-13y+16│+│x+3y-2│=0,那么点P(x,y)在第几象限 点Q(x+1,y-1)在坐标平面内的什么位置
七、实践探究
如图4所示,图中的能走遍棋盘中的任何一个位置吗 若不能,指出哪些位置无法走到;若能,请说明原因.
毛
学习目标
认识平面直角坐标系,了解点的坐标的意义,会用坐标表示点,能画出点的坐标位
渗透对应关系,提高学生的数感.
教学重点与难点
重点:平面直角坐标系和点的坐标.
难点:正确画坐标和找对应点.
教学过程:
一.利用已有知识,引入
1.如图,怎样说明数轴上点A和点B的位置,
2.根据下图,你能正确说出各个象棋子的位置吗?
二.明确概念
平面直角坐标系:平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系(rectangular coordinate system).水平的数轴称为x轴(x-axis)或横轴,习惯上取向右为正方向;竖直的数轴为y轴(y-axis)或纵轴,取向上方向为正方向;两个坐标轴的交点为平面直角坐标系的原点。
点的坐标:我们用一对有序数对表示平面上的点,这对数叫坐标。表示方法为(a,b).a是点对应横轴上的数值,b是点在纵轴上对应的数值。
例1 写出图中A、B、C、D点的坐标。
建立平面直角坐标系后,平面被坐标轴分成四部分,分别叫第一象限,第二象限,第三象限和第四象限。
你能说出例1中各点在第几象限吗?
例2 在平面直角坐标系中描出下列各点。
()A(3,4);B(-1,2);C(-3,-2);D(2,-2)
问题1:各象限点的坐标有什么特征?
练习:教材49页:练习1,2。
三.深入探索
教材48页:探索:
识别坐标和点的位置关系,以及由坐标判断两点的关系以及两点所确定的直线的位置关系。
[巩固练习]
教材49页习题6.1——第1题
教材50页——第2,4,5,6。
[小结]
平面直角坐标系;
点的坐标及其表示
各象限内点的坐标的特征
坐标轴上的点的坐标特征
平行于X轴的直线上点的坐标特征
平行于Y轴的直线上点的坐标特征
关于X轴对称的点坐标特征
关于X轴对称的点坐标特征
关于原点对称的点坐标特征
坐标的简单应用
[作业]
必做题:教科书50页:3题
(教材51页综合运用7,8,9,10为练习课内容)
6.1.2 检测题
一、选择题:
1.如图1所示,点A的坐标是 ( )毛
A.(3,2); B.(3,3); C.(3,-3) ; D.(-3,-3)
2.如图1所示,横坐标和纵坐标都是负数的点是 ( ) A.A点 B.B点 C.C点 D.D点
3.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B C.点C D.点D
4.若点M的坐标是(a,b),且a>0,b<0,则点M在( )
A.第一象限;B.第二象限; C.第三象限;D.第四象限
二、填空题:
1.如图2所示,点A的坐标为_______,点A关于x轴的对称点B的坐标为______, 点B关于y轴的对称点C的坐标为________.
2.在坐标平面内,已知点A(4,-6),那么点A关于x轴的对称点A ′的坐标为_____,点A关于y轴的对称点A″的坐标为_______.
3.在坐标平面内,已知点A(a,b),那么点A关于x轴的对称点A ′的坐标为______,点A关于y轴的对称点A″的坐标为_____.
4.点A(-3,2)在第_______象限,点D(-3,-2)在第_______象限,点C( 3, 2) 在第______象限,点D(-3,-2)在第_______象限,点E(0,2)在______轴上, 点F( 2, 0) 在______轴上.
5.已知点M(a,b),当a>0,b>0时,M在第_______象限;当a____,b______时,M 在第二象限;当a_____,b_______时,M在第四象限;当a<0,b<0时,M在第______象限.
三、基础训练:(共12分)
如果点A的坐标为(a2+1,-1-b2),那么点A在第几象限 为什么
四、提高训练:
如果点A(t-3s,2t+2s),B(14-2t+s,3t+2s-2)关于x轴对称,求s,t的值.
五、探索发现:
如图所示,C,D两点的横坐标分别为2,3,线段CD=1;B,D两点的横坐标分别为-2,3,线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1.
(1)如果x轴上有两点M(x1,0),N(x2,0)(x1
如果│3x-13y+16│+│x+3y-2│=0,那么点P(x,y)在第几象限 点Q(x+1,y-1)在坐标平面内的什么位置
七、实践探究
如图4所示,图中的能走遍棋盘中的任何一个位置吗 若不能,指出哪些位置无法走到;若能,请说明原因.
毛
