北师大版八上数学 1.1.1 认识勾股定理 课件(共20张)
文档属性
| 名称 | 北师大版八上数学 1.1.1 认识勾股定理 课件(共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览

文档简介
(共20张PPT)
1.1
探索勾股定理
第1课时
认识勾股定理
第一章
勾股定理
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
勾股定理
勾股定理与图形的面积
课时导入
复习提问
引出问题
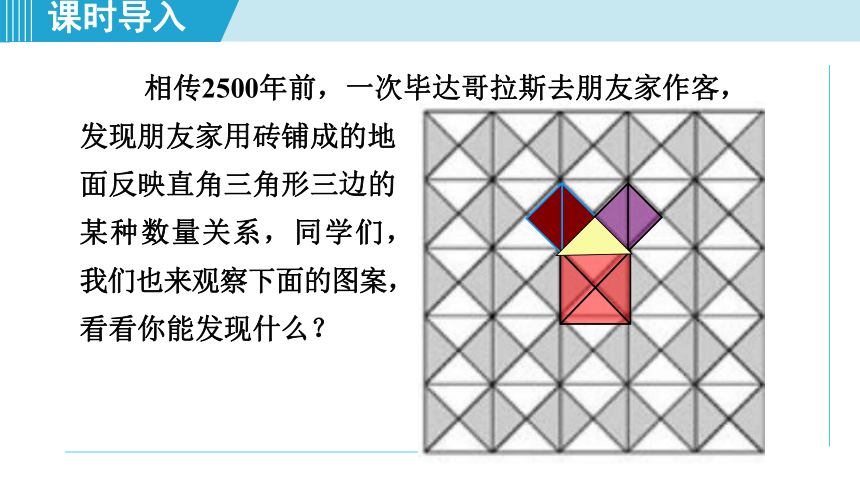
相传2500年前,一次毕达哥拉斯去朋友家作客,
发现朋友家用砖铺成的地
面反映直角三角形三边的
某种数量关系,同学们,
我们也来观察下面的图案,
看看你能发现什么?
课时导入
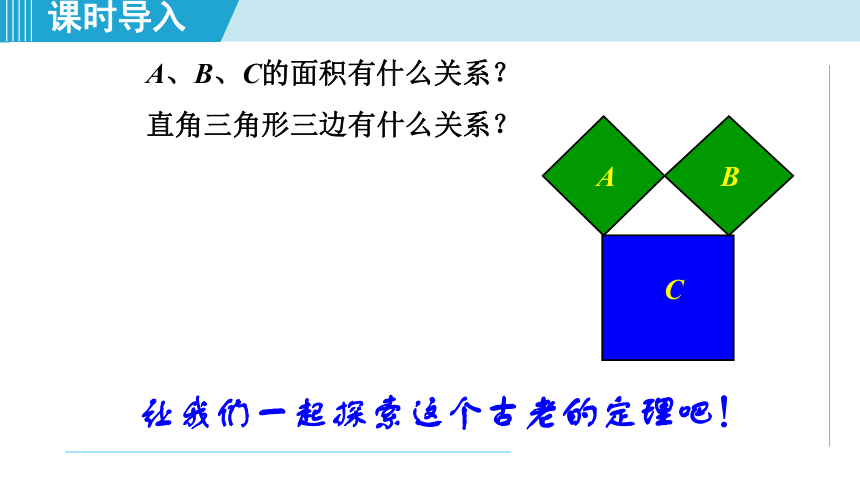
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
让我们一起探索这个古老的定理吧!
弦
股
勾
知识点
勾股定理
知1-导
感悟新知
1
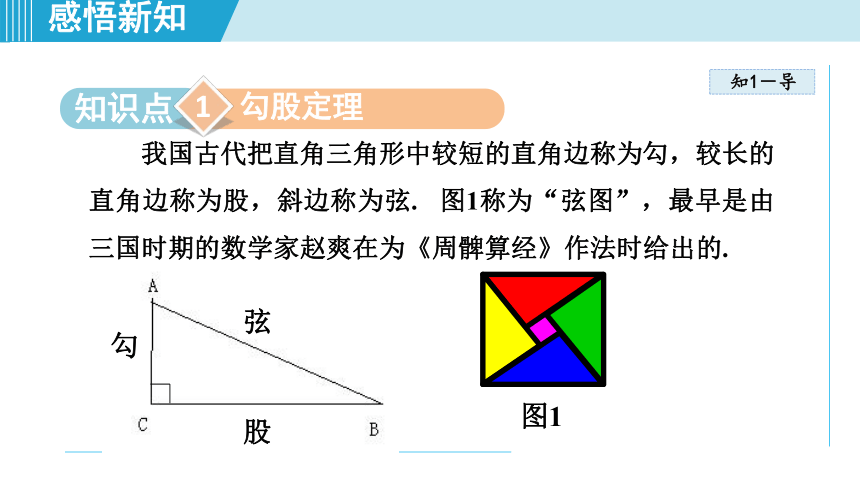
我国古代把直角三角形中较短的直角边称为勾,较长的
直角边称为股,斜边称为弦.
图1称为“弦图”,最早是由
三国时期的数学家赵爽在为《周髀算经》作法时给出的.
图1
知1-讲
感悟新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
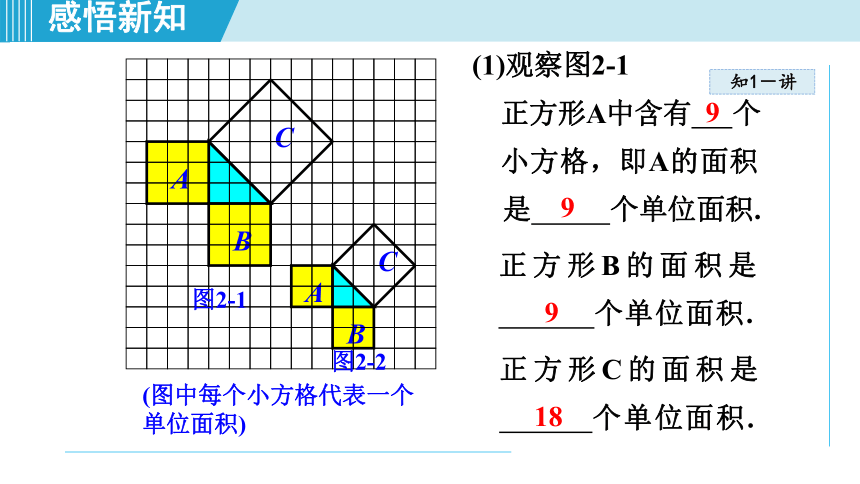
(1)观察图2-1
正方形A中含有
个
小方格,即A的面积
是
个单位面积.
正方形B的面积是
个单位面积.
正方形C的面积是
个单位面积.
9
9
9
18
知1-讲
感悟新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
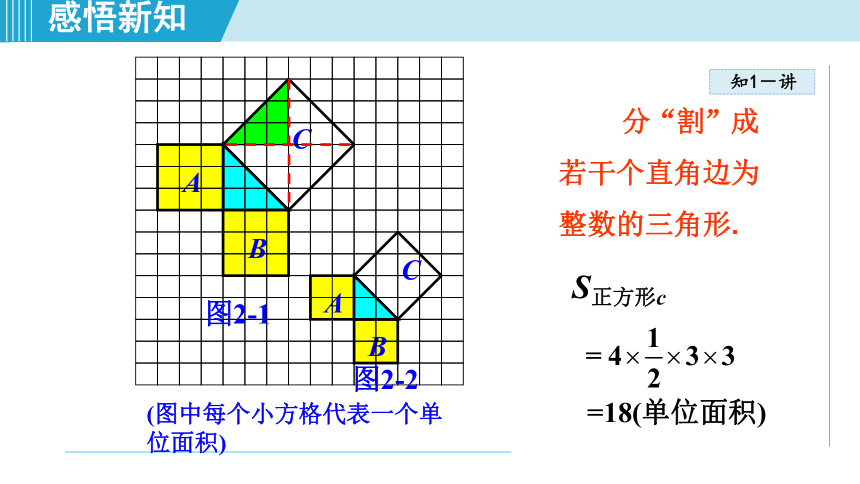
分“割”成若干个直角边为整数的三角形.
=18(单位面积)
S正方形c
知1-讲
感悟新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
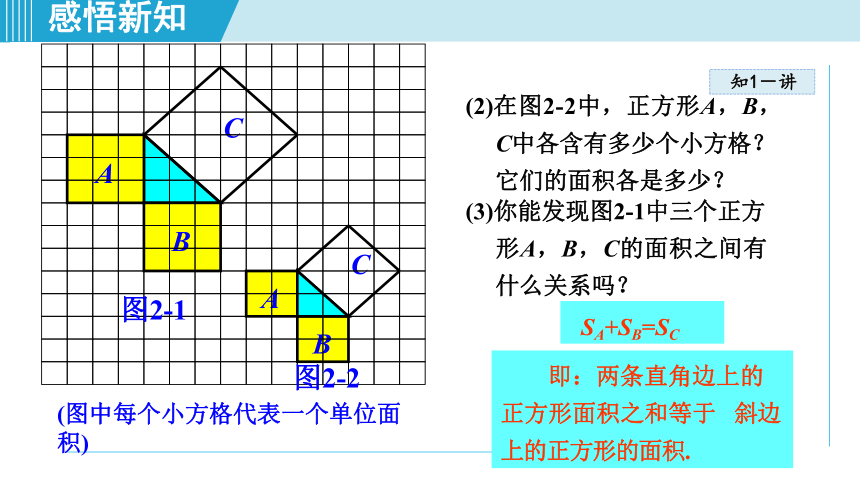
(2)在图2-2中,正方形A,B,
C中各含有多少个小方格?
它们的面积各是多少?
(3)你能发现图2-1中三个正方
形A,B,C的面积之间有
什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积.
A
B
C
a
c
b
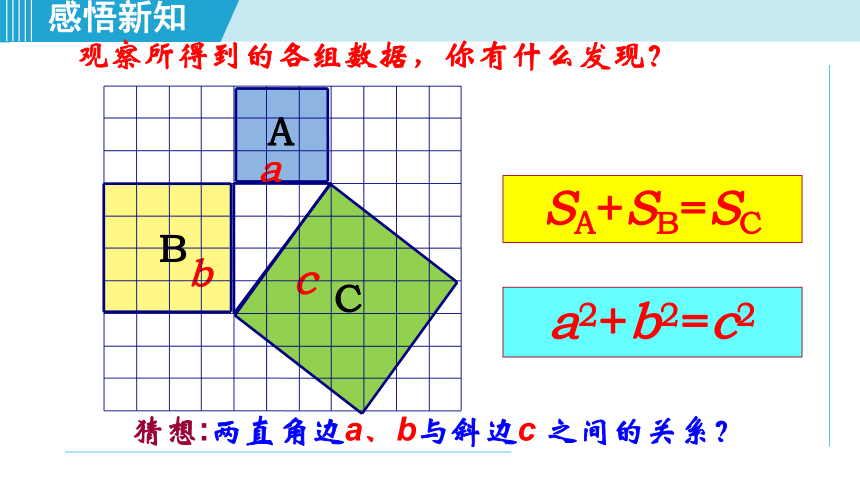
SA+SB=SC
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c
之间的关系?
a2+b2=c2
感悟新知
感悟新知
知1-讲
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
感悟新知
知1-讲
定理:
直角三角形两直角边的平方和等于斜边的平方.
如果用a,b和c分别表示直角三角形的两直角边
和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,
AC=b,BC=a,则a2+b2=c2.
如图,
感悟新知
知1-练
在Rt△ABC中,
∠A,∠B,∠C
的对边分
别为a,b,c,
∠
C=90°.
(1)已知a=3,b=4,
求c;
(2)已知c=13,a=5,求b;
(3)已知a
∶
b=3
∶
4,c=10,求b.
导引:
紧扣勾股定理及其变形公式解答.
例
1
感悟新知
知1-练
解:(1)因为∠C=90°,a=3,b=4,
所以由勾股定理,得c2=a2+b2=32+42=25,所以c=5.
(2)因为∠C=90°,c=13,a=5,
所以由勾股定理,得b2=c2-a2=132-52=144,所以b=12.
(3)因为a
∶
b=3
∶
4,
所以b=
a.
因为∠C=90°,c=10,b=
a,所以由勾股定理,得
a2+(
a)2=
102,解得a=6(负值舍去).
所以b=8.
知1-讲
总
结
感悟新知
分清待求的是斜边还是直角边,以便合理选
择直接用勾股定理,
还是用变形公式.
若求斜边,
则直接用勾股定理;若求直角边,则用变形公式.
知识点
勾股定理与图形的面积
知2-练
感悟新知
2
观察如图所示的图形,回答问题:
(1)如图①,△
DEF
为直角三角形,正方形P
的面积
为9,正方形Q
的面积为15,则正方形M
的面积为____
;
(2)如图②,分别以直角三角形ABC
的三边为直径向三角形外作三个半圆,则这三个半圆形的面积之间的关系式是_________
(用图中字母表示);
例2
感悟新知
知2-练
(3)如图③,如果直角三角形两直角边的长分别为3
和
4,分别以直角三角形的三边为直径作
半圆,请你利用
(2)中得出的结论求阴
影部分的面积.
导引:紧扣勾股定理所揭示的图形面积之间的关系解答.
感悟新知
知2-练
解:(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,
三角形的面积为S△,则S阴影=S1+S2+S△
-S3=S△
=
×3×4=6.
知2-讲
总
结
感悟新知
与直角三角形三边相连的正方形、半圆及正多
边形、圆都具有相同的结论:两直角边上图形面积的
和等于斜边上图形的面积.
课堂小结
勾股定理
1.
勾股定理的适用条件:直角三角形;它反映了直角
三角形三边关系.
2.由勾股定理的基本关系式:a2+b2=c2可得到一些
变形关系式:c2=a2+b2=(a+b)2-2ab=(a-b)2
+2ab;a2=c2-b2=(c+b)(c-b)等.
必做:
请完成教材课后习题
课后作业
作业
1.1
探索勾股定理
第1课时
认识勾股定理
第一章
勾股定理
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
勾股定理
勾股定理与图形的面积
课时导入
复习提问
引出问题
相传2500年前,一次毕达哥拉斯去朋友家作客,
发现朋友家用砖铺成的地
面反映直角三角形三边的
某种数量关系,同学们,
我们也来观察下面的图案,
看看你能发现什么?
课时导入
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
A
B
C
让我们一起探索这个古老的定理吧!
弦
股
勾
知识点
勾股定理
知1-导
感悟新知
1
我国古代把直角三角形中较短的直角边称为勾,较长的
直角边称为股,斜边称为弦.
图1称为“弦图”,最早是由
三国时期的数学家赵爽在为《周髀算经》作法时给出的.
图1
知1-讲
感悟新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(1)观察图2-1
正方形A中含有
个
小方格,即A的面积
是
个单位面积.
正方形B的面积是
个单位面积.
正方形C的面积是
个单位面积.
9
9
9
18
知1-讲
感悟新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
分“割”成若干个直角边为整数的三角形.
=18(单位面积)
S正方形c
知1-讲
感悟新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(2)在图2-2中,正方形A,B,
C中各含有多少个小方格?
它们的面积各是多少?
(3)你能发现图2-1中三个正方
形A,B,C的面积之间有
什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积.
A
B
C
a
c
b
SA+SB=SC
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c
之间的关系?
a2+b2=c2
感悟新知
感悟新知
知1-讲
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理
(毕达哥拉斯定理)
感悟新知
知1-讲
定理:
直角三角形两直角边的平方和等于斜边的平方.
如果用a,b和c分别表示直角三角形的两直角边
和斜边,那么a2+b2=c2.
数学表达式:
在Rt△ABC中,∠C=90°,AB=c,
AC=b,BC=a,则a2+b2=c2.
如图,
感悟新知
知1-练
在Rt△ABC中,
∠A,∠B,∠C
的对边分
别为a,b,c,
∠
C=90°.
(1)已知a=3,b=4,
求c;
(2)已知c=13,a=5,求b;
(3)已知a
∶
b=3
∶
4,c=10,求b.
导引:
紧扣勾股定理及其变形公式解答.
例
1
感悟新知
知1-练
解:(1)因为∠C=90°,a=3,b=4,
所以由勾股定理,得c2=a2+b2=32+42=25,所以c=5.
(2)因为∠C=90°,c=13,a=5,
所以由勾股定理,得b2=c2-a2=132-52=144,所以b=12.
(3)因为a
∶
b=3
∶
4,
所以b=
a.
因为∠C=90°,c=10,b=
a,所以由勾股定理,得
a2+(
a)2=
102,解得a=6(负值舍去).
所以b=8.
知1-讲
总
结
感悟新知
分清待求的是斜边还是直角边,以便合理选
择直接用勾股定理,
还是用变形公式.
若求斜边,
则直接用勾股定理;若求直角边,则用变形公式.
知识点
勾股定理与图形的面积
知2-练
感悟新知
2
观察如图所示的图形,回答问题:
(1)如图①,△
DEF
为直角三角形,正方形P
的面积
为9,正方形Q
的面积为15,则正方形M
的面积为____
;
(2)如图②,分别以直角三角形ABC
的三边为直径向三角形外作三个半圆,则这三个半圆形的面积之间的关系式是_________
(用图中字母表示);
例2
感悟新知
知2-练
(3)如图③,如果直角三角形两直角边的长分别为3
和
4,分别以直角三角形的三边为直径作
半圆,请你利用
(2)中得出的结论求阴
影部分的面积.
导引:紧扣勾股定理所揭示的图形面积之间的关系解答.
感悟新知
知2-练
解:(1)24
(2)S1+S2=S3
(3)设两个小半圆形的面积分别为S1,S2,大半圆
形的面积为S3,
三角形的面积为S△,则S阴影=S1+S2+S△
-S3=S△
=
×3×4=6.
知2-讲
总
结
感悟新知
与直角三角形三边相连的正方形、半圆及正多
边形、圆都具有相同的结论:两直角边上图形面积的
和等于斜边上图形的面积.
课堂小结
勾股定理
1.
勾股定理的适用条件:直角三角形;它反映了直角
三角形三边关系.
2.由勾股定理的基本关系式:a2+b2=c2可得到一些
变形关系式:c2=a2+b2=(a+b)2-2ab=(a-b)2
+2ab;a2=c2-b2=(c+b)(c-b)等.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
