冀教版七上数学 1.3.1绝对值与相反数的认识课件(19张)
文档属性
| 名称 | 冀教版七上数学 1.3.1绝对值与相反数的认识课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 18:42:56 | ||
图片预览






文档简介
(共19张PPT)
1.3
绝对值与相反数
第1课时
绝对值与相反
数的认识
第一章
有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
绝对值的定义
相反数的定义
课时导入
复习提问
引出问题
复习提问
引出问题
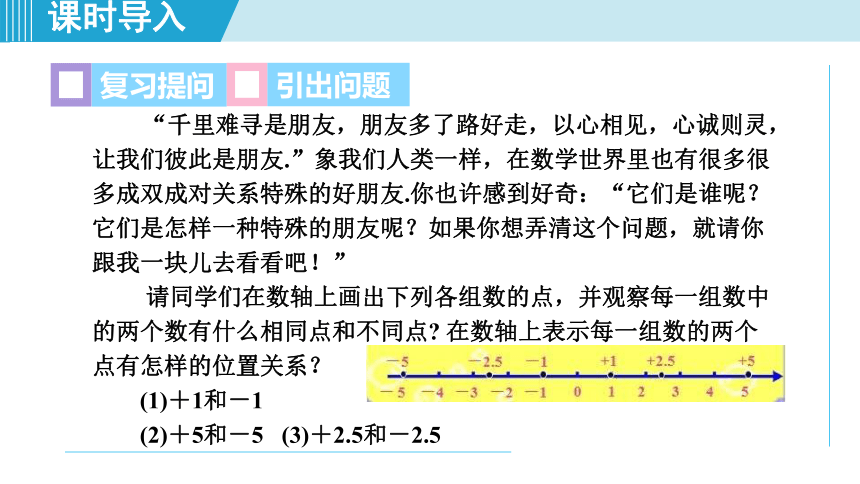
“千里难寻是朋友,朋友多了路好走,以心相见,心诚则灵,让我们彼此是朋友.”象我们人类一样,在数学世界里也有很多很多成双成对关系特殊的好朋友.你也许感到好奇:“它们是谁呢?它们是怎样一种特殊的朋友呢?如果你想弄清这个问题,就请你跟我一块儿去看看吧!”
请同学们在数轴上画出下列各组数的点,并观察每一组数中的两个数有什么相同点和不同点?
在数轴上表示每一组数的两个点有怎样的位置关系?
(1)+1和-1
(2)+5和-5
(3)+2.5和-2.5
知识点
绝对值的定义
知1-导
感悟新知
1
画一条数轴,在数轴上标出表示4,-2,
0的
点,并写出这些点到原点的距离.
知1-讲
归
纳
感悟新知
在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值.
如数a的绝对值可记作|a|,读作a的绝对值.
因为距离不可能是负数,所以一个数的绝对值一定是一个非负数
知1-讲
感悟新知
方法点拨
绝对值即“距离”,数轴上表示一个数的点离原点越远,则这个数的绝对值越大;反之,数轴上表示一个数的点离原点越近,则这个数的绝对值越小
知1-练
感悟新知
例
1
在数轴上标出表示下列各数的点,并写出它们的绝对值.
2.5,6,-4,-1.5,0.
解:如下图.
2.5的绝对值是2.5,6的绝对值是6,-4的绝对值是4,-1.5的绝对值是1.5,0的绝对值是0,即|2.5|=2.5,|6|=6,|-4|=4,|-1.5|=1.5,|0|=0.
-6
-5
-1
-2
-3
-4
0
1
2
3
4
5
6
7
知1-讲
总
结
感悟新知
本题运用了定义法,首先要在数轴上表示出各
数,然后观察各点到原点的距离,即可得到各数的
绝对值.
知1-练
感悟新知
1.在数轴上标出表示下列各数的点,并写出它们的绝对值.
2.5,6,-4,-1.5,0.
解:如图.
|2.5|=2.5,|6|=6,|-4|=4,
|-1.5|=1.5,|0|=0.
知1-练
感悟新知
2.
【中考·连云港】数轴上表示-2的点与原点的距
离是________.
3.
【中考·泉州】-3的绝对值是( )
A.3
B.-3
C.-
D.
2
A
知2-导
感悟新知
知识点
相反数的定义
2
(1)相反数的几何定义:在数轴上表示两个数的点,如果分别位于原点两侧,并且到原点的距离相等,那么这两个数互为相反数.如图所示,4与-4互为相反数,
互为相反数.
在数轴上,表示互为相反数的两点,位于原点的两侧,并且到原点的距离相等,也就是说,它们相对原点的位置只有方向不同.
(2)相反数的代数定义:符号不同、绝对值相等的两个数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数.
0的相反数是0.
知2-讲
感悟新知
特别解读
数轴上与原点的距离是
a(a是一个正数)的点有两个,分别在原点的左右两边,它们表示的数互为相反数
.
知2-讲
感悟新知
归
纳
像3和-3,5和-5,
等这样符号不同、
绝对值相等的两个数,我们称其中一个数是另一个
数的相反数,这两个数互为相反数.
0的相反数规
定为0.
知2-练
感悟新知
例2
下列说法正确的是( )
A.-2是相反数
B.-
与-2互为相反数
C.-3与+2互为相反数
D.-
与0.5互为相反数
导引:判断两个数是否互为相反数,按其定义从两
个方面去看:符号(+,-)和符号后面的数(相同).
D
知2-讲
感悟新知
总
结
(
1
)相反数不能单独存在,前提是“互为”.
(
2
)判断两个数是否互为相反数,要从两个方面看,一是符号不能相同;二是符号后面的数一定要相同.
知2-练
感悟新知
1.
下列说法正确的是( )
A.因为相反数是成对出现的,所以0没有
相反数
B.符号不同的两个数互为相反数
C.正数与负数互为相反数
D.只有0的相反数是它本身,
D
知2-练
感悟新知
2.【中考·广东】-2的相反数是( )
A.2
B.-2
C.
D.-
3.【中考·广元】一个数的相反数是3,这个数
是( )
A.
B.-
C.3
D.-3
A
D
课堂小结
绝对值与相反数的认识
1.相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a的相
反数是-a,特殊的:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个
点所表示的数互为相反数.
2.多重符号化简的方法规律:
方法一:把所有的正号去掉;负号的个数是偶数时结
果为正,是奇数时结果为负,即“奇负偶正”.
方法二:采用两个同号得正,异号得负,分成化简.
必做:
请完成教材课后习题
课后作业
作业
1.3
绝对值与相反数
第1课时
绝对值与相反
数的认识
第一章
有理数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
绝对值的定义
相反数的定义
课时导入
复习提问
引出问题
复习提问
引出问题
“千里难寻是朋友,朋友多了路好走,以心相见,心诚则灵,让我们彼此是朋友.”象我们人类一样,在数学世界里也有很多很多成双成对关系特殊的好朋友.你也许感到好奇:“它们是谁呢?它们是怎样一种特殊的朋友呢?如果你想弄清这个问题,就请你跟我一块儿去看看吧!”
请同学们在数轴上画出下列各组数的点,并观察每一组数中的两个数有什么相同点和不同点?
在数轴上表示每一组数的两个点有怎样的位置关系?
(1)+1和-1
(2)+5和-5
(3)+2.5和-2.5
知识点
绝对值的定义
知1-导
感悟新知
1
画一条数轴,在数轴上标出表示4,-2,
0的
点,并写出这些点到原点的距离.
知1-讲
归
纳
感悟新知
在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值.
如数a的绝对值可记作|a|,读作a的绝对值.
因为距离不可能是负数,所以一个数的绝对值一定是一个非负数
知1-讲
感悟新知
方法点拨
绝对值即“距离”,数轴上表示一个数的点离原点越远,则这个数的绝对值越大;反之,数轴上表示一个数的点离原点越近,则这个数的绝对值越小
知1-练
感悟新知
例
1
在数轴上标出表示下列各数的点,并写出它们的绝对值.
2.5,6,-4,-1.5,0.
解:如下图.
2.5的绝对值是2.5,6的绝对值是6,-4的绝对值是4,-1.5的绝对值是1.5,0的绝对值是0,即|2.5|=2.5,|6|=6,|-4|=4,|-1.5|=1.5,|0|=0.
-6
-5
-1
-2
-3
-4
0
1
2
3
4
5
6
7
知1-讲
总
结
感悟新知
本题运用了定义法,首先要在数轴上表示出各
数,然后观察各点到原点的距离,即可得到各数的
绝对值.
知1-练
感悟新知
1.在数轴上标出表示下列各数的点,并写出它们的绝对值.
2.5,6,-4,-1.5,0.
解:如图.
|2.5|=2.5,|6|=6,|-4|=4,
|-1.5|=1.5,|0|=0.
知1-练
感悟新知
2.
【中考·连云港】数轴上表示-2的点与原点的距
离是________.
3.
【中考·泉州】-3的绝对值是( )
A.3
B.-3
C.-
D.
2
A
知2-导
感悟新知
知识点
相反数的定义
2
(1)相反数的几何定义:在数轴上表示两个数的点,如果分别位于原点两侧,并且到原点的距离相等,那么这两个数互为相反数.如图所示,4与-4互为相反数,
互为相反数.
在数轴上,表示互为相反数的两点,位于原点的两侧,并且到原点的距离相等,也就是说,它们相对原点的位置只有方向不同.
(2)相反数的代数定义:符号不同、绝对值相等的两个数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数.
0的相反数是0.
知2-讲
感悟新知
特别解读
数轴上与原点的距离是
a(a是一个正数)的点有两个,分别在原点的左右两边,它们表示的数互为相反数
.
知2-讲
感悟新知
归
纳
像3和-3,5和-5,
等这样符号不同、
绝对值相等的两个数,我们称其中一个数是另一个
数的相反数,这两个数互为相反数.
0的相反数规
定为0.
知2-练
感悟新知
例2
下列说法正确的是( )
A.-2是相反数
B.-
与-2互为相反数
C.-3与+2互为相反数
D.-
与0.5互为相反数
导引:判断两个数是否互为相反数,按其定义从两
个方面去看:符号(+,-)和符号后面的数(相同).
D
知2-讲
感悟新知
总
结
(
1
)相反数不能单独存在,前提是“互为”.
(
2
)判断两个数是否互为相反数,要从两个方面看,一是符号不能相同;二是符号后面的数一定要相同.
知2-练
感悟新知
1.
下列说法正确的是( )
A.因为相反数是成对出现的,所以0没有
相反数
B.符号不同的两个数互为相反数
C.正数与负数互为相反数
D.只有0的相反数是它本身,
D
知2-练
感悟新知
2.【中考·广东】-2的相反数是( )
A.2
B.-2
C.
D.-
3.【中考·广元】一个数的相反数是3,这个数
是( )
A.
B.-
C.3
D.-3
A
D
课堂小结
绝对值与相反数的认识
1.相反数的意义:
代数意义:(1)成对出现;(2)只有符号不同,即a的相
反数是-a,特殊的:0的相反数是0.
几何意义:数轴上原点两旁且到原点距离相等的两个
点所表示的数互为相反数.
2.多重符号化简的方法规律:
方法一:把所有的正号去掉;负号的个数是偶数时结
果为正,是奇数时结果为负,即“奇负偶正”.
方法二:采用两个同号得正,异号得负,分成化简.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
