三角形全等的判定
图片预览


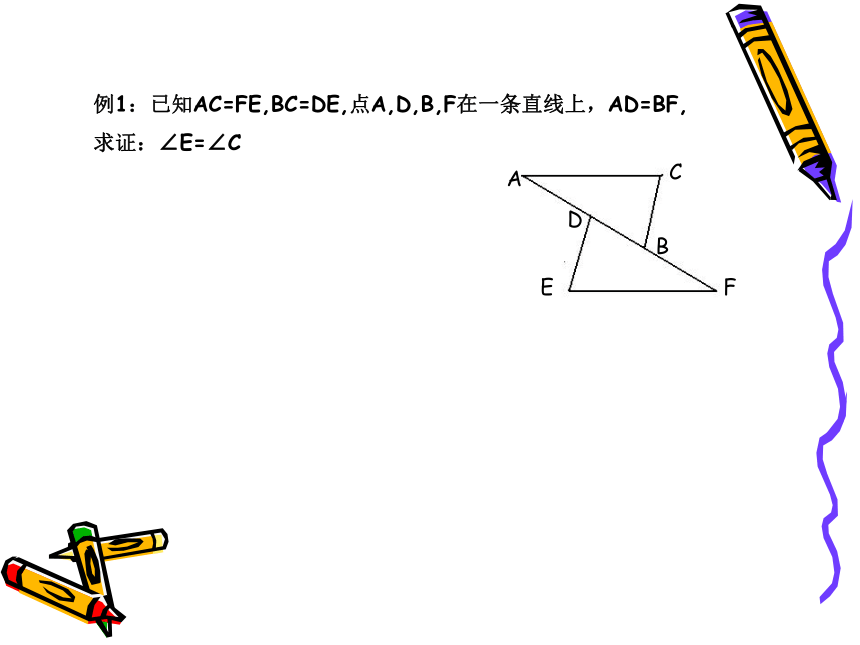
文档简介
(共27张PPT)
三角形全等的条件(复习)
知识梳理:
1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2:全等三角形有哪些性质?
3:三角形全等的判定方法有哪些?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
(3):全等三角形的对应边上的对应中线、角平分线、高线分别相等。
SSS、SAS、ASA、AAS、HL(RT△)
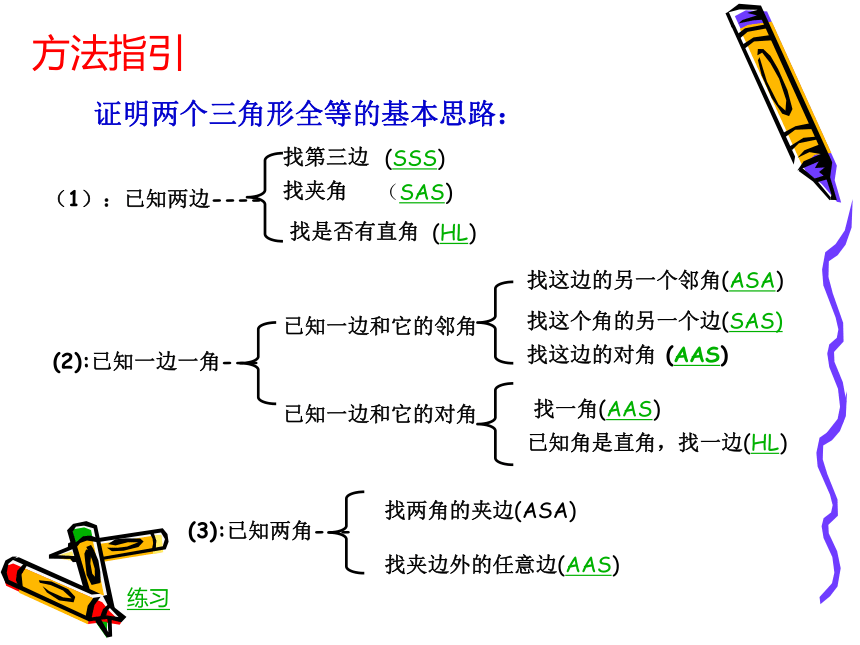
方法指引
证明两个三角形全等的基本思路:
(1):已知两边----
找第三边
(SSS)
找夹角
(SAS)
(2):已知一边一角---
已知一边和它的邻角
找是否有直角
(HL)
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
找一角(AAS)
已知角是直角,找一边(HL)
(3):已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
练习
例1:已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=BF,
求证:∠E=∠C
A
B
D
F
E
C
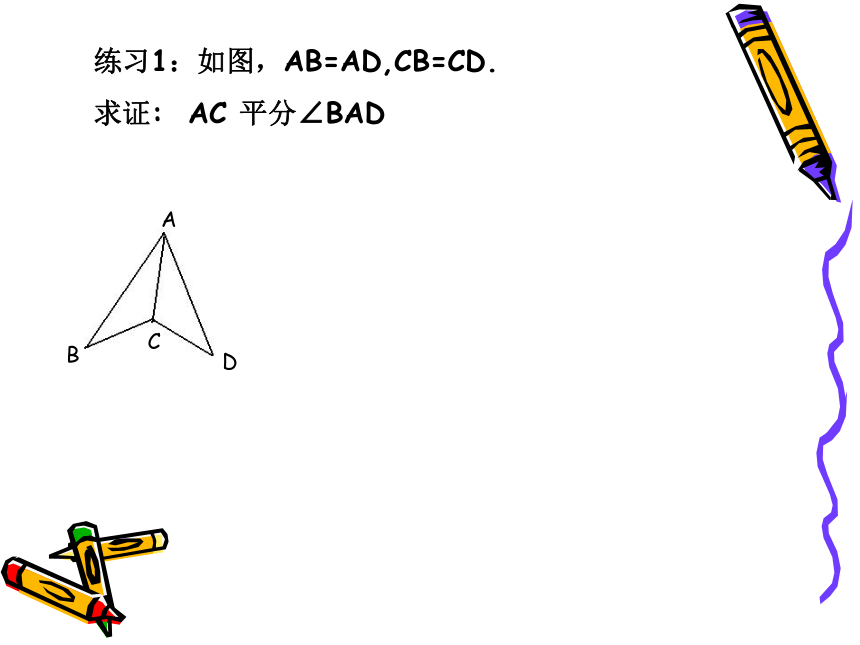
练习1:如图,AB=AD,CB=CD.
求证: AC 平分∠BAD
A
D
C
B
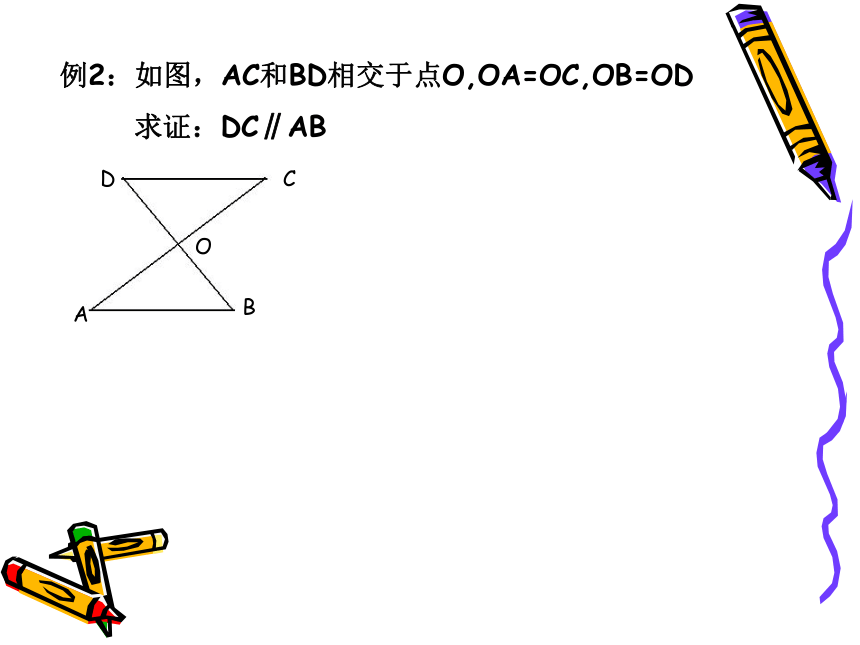
例2:如图,AC和BD相交于点O,OA=OC,OB=OD
求证:DC∥AB
A
O
D
B
C
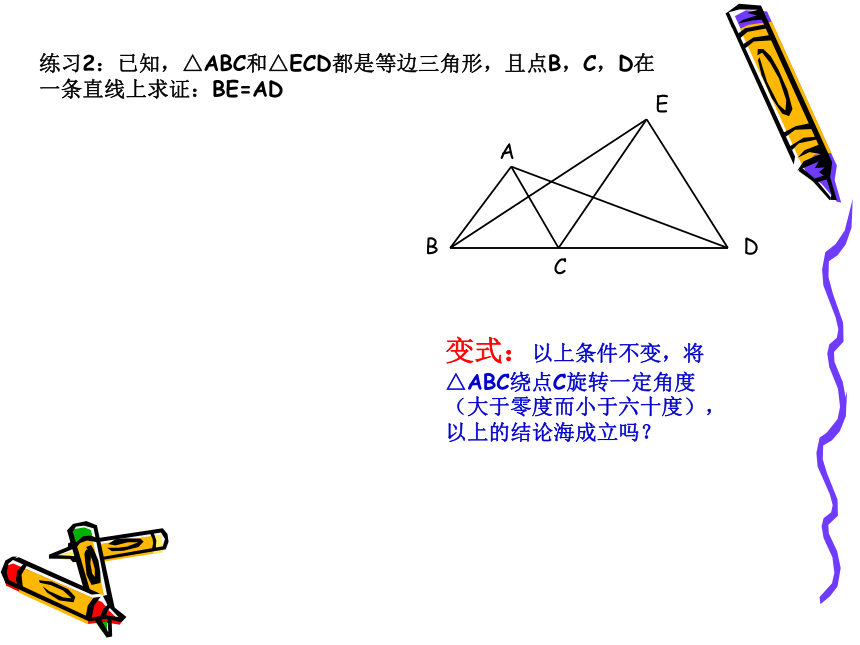
练习2:已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
E
D
C
A
B
变式:以上条件不变,将△ABC绕点C旋转一定角度(大于零度而小于六十度),以上的结论海成立吗?
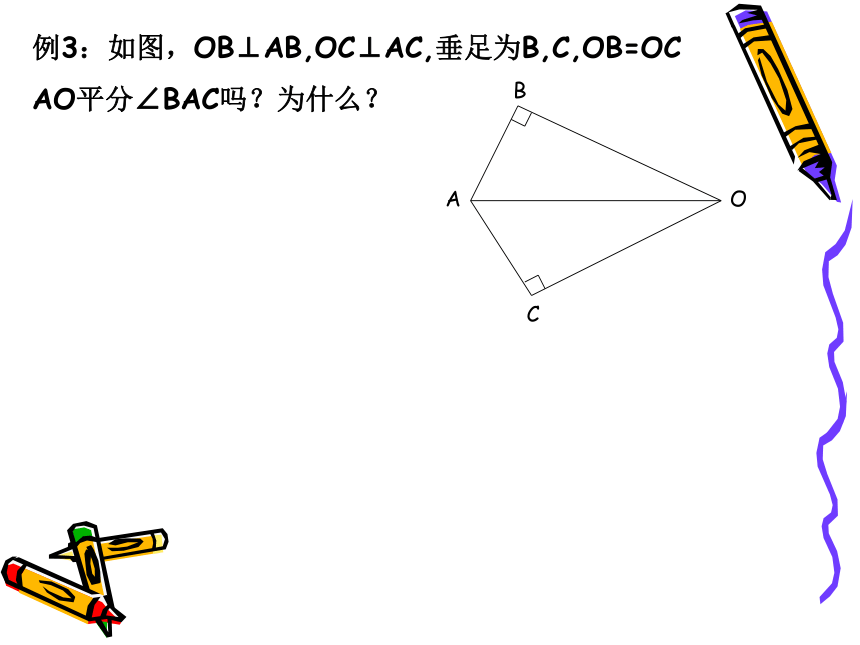
例3:如图,OB⊥AB,OC⊥AC,垂足为B,C,OB=OC
AO平分∠BAC吗?为什么?
O
C
B
A
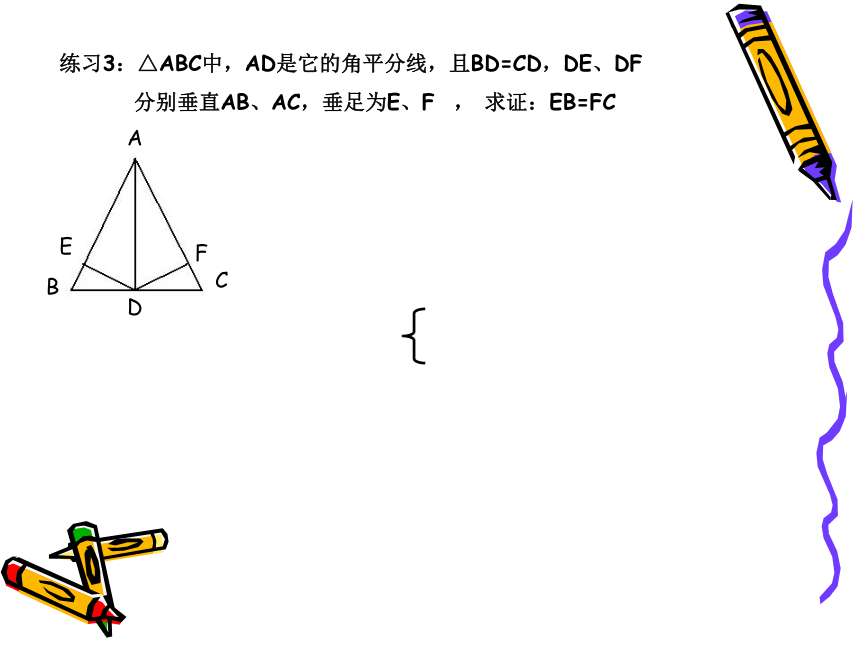
练习3:△ABC中,AD是它的角平分线,且BD=CD,DE、DF
分别垂直AB、AC,垂足为E、F , 求证:EB=FC
F
E
D
C
B
A
例4:如图,D在AB上,E在AC上,AB=AC ,
∠B=∠C, 试问AD=AE吗?为什么?
E
D
C
B
A
练习4: 如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带那块去合适?为什么?
B
A
AB
例5:已知 AC=DB, ∠1=∠2.
求证: ∠A=∠D
2
1
D
C
B
A
练习5:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
4
3
2
1
E
D
C
B
A
例6:如图所示,AB与CD相交于点O, ∠A=∠B,OA=OB 添加条件 所以 △AOC≌△BOD 理由是
A
O
D
C
B
∠C=∠D
∠AOC=∠BOD
AAS
ASA
E
D
C
B
A
例7:如图所示,AB=AD,∠E=∠C
要想使△ABC≌△ADE可以添加的条
件是
依据是
∠EDA=∠B
∠DAE=∠BAC
∠BAD=∠EAC
AAS
例8:如图,已知AB=CD,DE⊥AC,BF⊥AC,AE=CF
求证:△ABF≌△CDE
F
E
D
C
B
A
F
E
D
C
B
A
例9:如图,已知AC∥EF,DE∥BA,若使△ABC≌△EDF,还需要补
充的条件可以是
或
或
或
AB=ED
AC=EF
BC=DF
DC=BF
返回
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
△ABF≌△DEC
△CBF≌△FEC
△ABC≌△DEF
答:
练2
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
△ABF≌△DEC
答:
证明:
∵ AB∥DE
∴ ∠A=∠D
在△ABF和△DEC 中
AB=DE
∠A=∠D
AF=DC
∴ △ABF≌△DEC (SAS)
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
△ABF≌△DEC
答:
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
答:
△ABC≌△DEF
证明:
∵ AB∥DE
∴ ∠A=∠D
∵ AF=DC
∴ AF+FC=DC+FC
∴ AC=DF
在△ABC和△DEF中
AC=DF
∠A=∠D
AB=DE
∴ △ABC≌△DEF (SAS)
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
答:
△CBF≌△FEC
证明:
∵ △ABC≌△DEF
∴ BC=EF
∵ △ABF≌△DEC
∴ BF=EC
在△CBF和△FEC中
BF=EC
BC=EF
CF=FC
∴ △CBF≌△FEC (SSS)
练习
2:如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知: EG∥AF
求证:
G
F
E
D
C
B
A
高
3:如图,AB∥A′B′,AC∥A′C′,且BB′=CC′你能说明AC=A′C′的理由吗?
C′
C
B′
A′
B
A
练习
高
总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
交流平台
本节课你还有理解不透澈的地方吗?
祝同学们学习进步
再见
三角形全等的条件(复习)
知识梳理:
1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2:全等三角形有哪些性质?
3:三角形全等的判定方法有哪些?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
(3):全等三角形的对应边上的对应中线、角平分线、高线分别相等。
SSS、SAS、ASA、AAS、HL(RT△)
方法指引
证明两个三角形全等的基本思路:
(1):已知两边----
找第三边
(SSS)
找夹角
(SAS)
(2):已知一边一角---
已知一边和它的邻角
找是否有直角
(HL)
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
找一角(AAS)
已知角是直角,找一边(HL)
(3):已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
练习
例1:已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=BF,
求证:∠E=∠C
A
B
D
F
E
C
练习1:如图,AB=AD,CB=CD.
求证: AC 平分∠BAD
A
D
C
B
例2:如图,AC和BD相交于点O,OA=OC,OB=OD
求证:DC∥AB
A
O
D
B
C
练习2:已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
E
D
C
A
B
变式:以上条件不变,将△ABC绕点C旋转一定角度(大于零度而小于六十度),以上的结论海成立吗?
例3:如图,OB⊥AB,OC⊥AC,垂足为B,C,OB=OC
AO平分∠BAC吗?为什么?
O
C
B
A
练习3:△ABC中,AD是它的角平分线,且BD=CD,DE、DF
分别垂直AB、AC,垂足为E、F , 求证:EB=FC
F
E
D
C
B
A
例4:如图,D在AB上,E在AC上,AB=AC ,
∠B=∠C, 试问AD=AE吗?为什么?
E
D
C
B
A
练习4: 如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带那块去合适?为什么?
B
A
AB
例5:已知 AC=DB, ∠1=∠2.
求证: ∠A=∠D
2
1
D
C
B
A
练习5:如图,已知E在AB上,∠1=∠2, ∠3=∠4,那么AC等于AD吗?为什么?
4
3
2
1
E
D
C
B
A
例6:如图所示,AB与CD相交于点O, ∠A=∠B,OA=OB 添加条件 所以 △AOC≌△BOD 理由是
A
O
D
C
B
∠C=∠D
∠AOC=∠BOD
AAS
ASA
E
D
C
B
A
例7:如图所示,AB=AD,∠E=∠C
要想使△ABC≌△ADE可以添加的条
件是
依据是
∠EDA=∠B
∠DAE=∠BAC
∠BAD=∠EAC
AAS
例8:如图,已知AB=CD,DE⊥AC,BF⊥AC,AE=CF
求证:△ABF≌△CDE
F
E
D
C
B
A
F
E
D
C
B
A
例9:如图,已知AC∥EF,DE∥BA,若使△ABC≌△EDF,还需要补
充的条件可以是
或
或
或
AB=ED
AC=EF
BC=DF
DC=BF
返回
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
△ABF≌△DEC
△CBF≌△FEC
△ABC≌△DEF
答:
练2
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
△ABF≌△DEC
答:
证明:
∵ AB∥DE
∴ ∠A=∠D
在△ABF和△DEC 中
AB=DE
∠A=∠D
AF=DC
∴ △ABF≌△DEC (SAS)
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
△ABF≌△DEC
答:
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
答:
△ABC≌△DEF
证明:
∵ AB∥DE
∴ ∠A=∠D
∵ AF=DC
∴ AF+FC=DC+FC
∴ AC=DF
在△ABC和△DEF中
AC=DF
∠A=∠D
AB=DE
∴ △ABC≌△DEF (SAS)
练习
1:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全等三角形?请任选一对给予证明。
F
E
D
C
B
A
答:
△CBF≌△FEC
证明:
∵ △ABC≌△DEF
∴ BC=EF
∵ △ABF≌△DEC
∴ BF=EC
在△CBF和△FEC中
BF=EC
BC=EF
CF=FC
∴ △CBF≌△FEC (SSS)
练习
2:如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。(只写出一种情况)①AB=AC ②DE=DF ③BE=CF
已知: EG∥AF
求证:
G
F
E
D
C
B
A
高
3:如图,AB∥A′B′,AC∥A′C′,且BB′=CC′你能说明AC=A′C′的理由吗?
C′
C
B′
A′
B
A
练习
高
总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
交流平台
本节课你还有理解不透澈的地方吗?
祝同学们学习进步
再见
