23.2 中心对称-2021-2022学年九年级数学上册高频易错必刷题汇编(人教版)(含答案)
文档属性
| 名称 | 23.2 中心对称-2021-2022学年九年级数学上册高频易错必刷题汇编(人教版)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 19:37:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
23.2 中心对称 高频易错必刷题汇编
一、选择题
1.(2021?徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
2.(2021?广元)下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )
A.医疗废物 B.中国红十字会
C.医疗卫生服务机构 D.国际急救
3.(2021?大连模拟)在平面直角坐标系中,点P,Q的坐标分别为(2,﹣3),(2,3),则点P与点Q( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=1对称
4.(2021?青岛_????¨?????????????_△ABC的3个顶点都在格点上,将△ABC先向左平移4个单位长度,再作关于原点O的中心对称图形,得到△A′B′C′,则点A的对应点A′的坐标是( )21教育网
A.(﹣3,﹣2) B.(﹣3,2) C.(2,﹣2) D.(3,﹣2)
5.(2021?淮安模拟)若点A(1+m,1﹣n)与点B(﹣3,2)关于原点对称,则m+n的值为( )
A.﹣1 B.2 C.3 D.5
6.(2021?宁波模拟)两_?????¨????????????_(非正方形)纸片按如图呈中心对称方式放置在一个大正方形内,记重叠部分为①,不重叠部分为②和③;若已知正方形面积,且图形①和图形③相似,则下列可求的是( )
A.矩形的面积 B.矩形的周长
C.图形①的面积 D.图形②的面积
7.(2021?长沙模拟)若点A(a+b,1)与点B(﹣5,a﹣b)关于原点对称,则点P(a,b)的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,﹣3) D.(﹣3,2)
8.(2020?市南二模)_??¨???é???????±???_点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(6,50°)或P(6,﹣310°)或P(6,410°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(6,﹣490°) B.Q(6,590°) C.Q(6,﹣110°) D.Q(6,230°)
9.(2021?_???????¨??????????_面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2020A2021B2021(n是正整数)的顶点A2021的坐标是( )21cnjy.com
A.(4041,) B.(4041,﹣) C.(4043,) D.(4043,﹣)
10.(2021?安_?????????????????¨_菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )www.21-cn-jy.com
A.3+ B.2+2 C.2+ D.1+2
二、填空题
11.(2020?西城模拟)请写出一个是中心对称图形而不是轴对称图形的多边形,它的名字可以是 .
12.(2021?临沂)在平面_???è§?????????????_,平行四边形ABCD的对称中心是坐标原点,顶点A、B的坐标分别是(﹣1,1)、(2,1),将平行四边形ABCD沿x轴向右平移3个单位长度,则顶点C的对应点C1的坐标是 .
13.(2021?淮_??¨?¨???????è§????_以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣2,3)]等于 .21·世纪*教育网
14.(2020_?????°????????????_,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(﹣1,1),C(3,1).△A'B'C′是△ABC关于x轴的对称图形,将△A'B'C'绕点B'逆时针旋转180°,点A'的对应点为M,则点M的坐标为 .www-2-1-cnjy-com
15.(2020?九_?±?????¨??????????_,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 °的角后,两张硬纸片所构成的图形是中心对称图形.
16.(2020?台州)用_???????¤§?????????_地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为 .(用含a,b的代数式表示)2-1-c-n-j-y
三、解答题
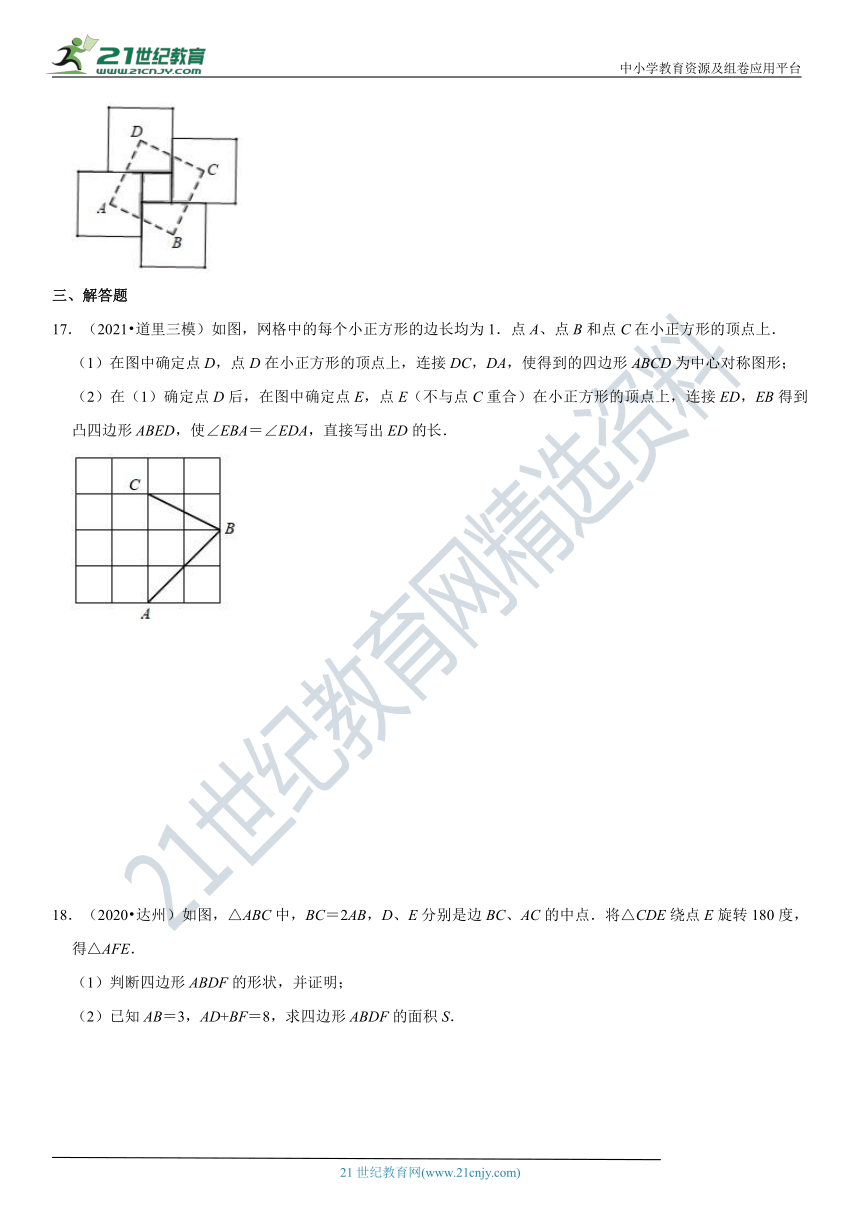
17.(2021?道里三模)如图,网格中的每个小正方形的边长均为1.点A、点B和点C在小正方形的顶点上.
(1)在图中确定点D,点D在小正方形的顶点上,连接DC,DA,使得到的四边形ABCD为中心对称图形;
(2)在(1)确定点D后,在_???????????????E_,点E(不与点C重合)在小正方形的顶点上,连接ED,EB得到凸四边形ABED,使∠EBA=∠EDA,直接写出ED的长.21教育名师原创作品
18.(2020?达州)如图,△ABC中,BC=2AB,D、E分别是边BC、AC的中点.将△CDE绕点E旋转180度,得△AFE.
(1)判断四边形ABDF的形状,并证明;
(2)已知AB=3,AD+BF=8,求四边形ABDF的面积S.
19.(2021?平江模拟)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
20.(2021?_???é???¨??????????_图,正方形OABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.【版权所有:21教育】
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方形BD_EF???????§°???_心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
23.2 中心对称 高频易错必刷题汇编
一、选择题
1.(2021?徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
解:A.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.是轴对称图形,也是中心对称图形,故此选项不符合题意;
C.不是轴对称图形,是中心对称图形,故此选项不符合题意;
D.是轴对称图形,不是中心对称图形,故此选项符合题意.
答案:D.
2.(2021?广元)下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )
A.医疗废物 B.中国红十字会
C.医疗卫生服务机构 D.国际急救
解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.既是轴对称图形又是中心对称图形,故此选项符合题意;
D.不是轴对称图形,也不是中心对称图形,故此选项不合题意.
答案:C.
3.(2021?大连模拟)在平面直角坐标系中,点P,Q的坐标分别为(2,﹣3),(2,3),则点P与点Q( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=1对称
解:因为点P(2,﹣3)与点Q(2,3)的横坐标相同,纵坐标互为相反数,
所以点P(2,﹣3)与点Q(2,3)关于x轴对称.
答案:A.
4.(2021?青岛二模)如图,_???ABC???3_个顶点都在格点上,将△ABC先向左平移4个单位长度,再作关于原点O的中心对称图形,得到△A′B′C′,则点A的对应点A′的坐标是( )
A.(﹣3,﹣2) B.(﹣3,2) C.(2,﹣2) D.(3,﹣2)
解:由题意可知A的坐标为A(1,2),
将△ABC先向左平移4个单位长度后点A的对应点坐标为(﹣3,2).
再作关于原点O的中心对称图形,得到△A′B′C′,则点A的对应点A′的坐标是(3,﹣2).
答案:D.
5.(2021?淮安模拟)若点A(1+m,1﹣n)与点B(﹣3,2)关于原点对称,则m+n的值为( )
A.﹣1 B.2 C.3 D.5
解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于原点对称,
∴1+m=3,1﹣n=﹣2,
解得:m=2,n=3,
则m+n的值为:2+3=5.
答案:D.
6.(2021?宁波模拟)两张_??¨???????????????_非正方形)纸片按如图呈中心对称方式放置在一个大正方形内,记重叠部分为①,不重叠部分为②和③;若已知正方形面积,且图形①和图形③相似,则下列可求的是( )
A.矩形的面积 B.矩形的周长
C.图形①的面积 D.图形②的面积
解:设正方形的边长为c,矩形的长,宽分别为a,b,则=,
化简得到,2a2﹣2b2=3ac﹣3bc,即2(a﹣b)(a+b)=3c(a﹣b),
∵a≠b,
∴2(a+b)=3c,
即矩形的周长为3c,
答案:B.
7.(2021?长沙模拟)若点A(a+b,1)与点B(﹣5,a﹣b)关于原点对称,则点P(a,b)的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,﹣3) D.(﹣3,2)
解:∵点A(a+b,1)与点B(﹣5,a﹣b)关于原点对称,
∴,
解得:,
故点P(a,b)的坐标是(2,3).
答案:A.
8.(202_0?????????????¨?_)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(6,50°)或P(6,﹣310°)或P(6,410°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(6,﹣490°) B.Q(6,590°) C.Q(6,﹣110°) D.Q(6,230°)
解:∵P(6,50°)或P(6,﹣310°)或P(6,410°),
∴由点P关于点O成中心对称的点Q可得:点Q的极坐标为(6,230°),(6,﹣490°),(6,590°),
答案:C.
9.(2021?河南模拟)平_é?????è§??????????_中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2020A2021B2021(n是正整数)的顶点A2021的坐标是( )21·cn·jy·com
A.(4041,) B.(4041,﹣) C.(4043,) D.(4043,﹣)
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为:(1,),B1的坐标为:(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣=﹣,
∴点A2的坐标是:(3,﹣),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣)=,
∴点A3的坐标是:(5,),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣=﹣,
∴点A4的坐标是:(7,﹣),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×4﹣1,…,
∴An的横坐标是:2n﹣1,A2n+1的横坐标是:2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是:,当n为偶数时,An的纵坐标是:﹣,
∴顶点A2n+1的纵坐标是:,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是:(4n+1,),
∴△B2020A2021B2021的顶点A2021的横坐标是:4×1010+1=4041,纵坐标是:,2·1·c·n·j·y
答案:A.
10.(2021?_??????????????????_在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )21*cnjy*com
A.3+ B.2+2 C.2+ D.1+2
解:如图,连接BD,AC.
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD=2,∠BAO=∠DAO=60°,BD⊥AC,
∴∠ABO=∠CBO=30°,
∴OA=AB=1,OB=OA=,
∵OE⊥AB,OF⊥BC,
∴∠BEO=∠BFO=90°,
在△BEO和△BFO中,
,
∴△BEO≌△BFO(AAS),
∴OE=OF,BE=BF,
∵∠EBF=60°,
∴△BEF是等边三角形,
∴EF=BE=×=,
同法可证,△DGH,△OEH,△OFG都是等边三角形,
∴EF=GH=,EH=FG=,
∴四边形EFGH的周长=3+,
答案:A.
二、填空题
11.(2020?西城模拟)请写出一个是中心对称图形而不是轴对称图形的多边形,它的名字可以是 平行四边形.(答案不唯一) .21世纪教育网版权所有
解:由平行四边形的性质可知,平行四边形是中心对称图形而不是轴对称图形.
答案:平行四边形(答案不唯一).
12.(2021?临_????????¨???é?????_角坐标系中,平行四边形ABCD的对称中心是坐标原点,顶点A、B的坐标分别是(﹣1,1)、(2,1),将平行四边形ABCD沿x轴向右平移3个单位长度,则顶点C的对应点C1的坐标是 (4,﹣1) .【来源:21·世纪·教育·网】
解:∵平行四边形ABCD的对称中心是坐标原点,
∴点A,点C关于原点对称,
∵A(﹣1,1),
∴C(1,﹣1),
∴将平行四边形ABCD沿x轴向右平移3个单位长度,则顶点C的对应点C1的坐标是(4,﹣1),
答案:(4,﹣1).
13.(20_21????·???¨?¨?_拟)规定以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣2,3)]等于 (2,3) .【出处:21教育名师】
解:∵①f(m,n)=(m,﹣n),②g(m,n)=(﹣m,﹣n),
∴g[f(﹣2,3)]=g(﹣2,﹣3)=(2,3).
答案:(2,3).
14.(2020?泰安)_??????????°???????_形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(﹣1,1),C(3,1).△A'B'C′是△ABC关于x轴的对称图形,将△A'B'C'绕点B'逆时针旋转180°,点A'的对应点为M,则点M的坐标为 (﹣2,1) .
解:将△A'B'C'绕点B'逆时针旋转180°,如图所示:
所以点M的坐标为(﹣2,1),
答案:(﹣2,1).
15.(2020?九江一模)如图_?????¤????????¨é??_合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 60 °的角后,两张硬纸片所构成的图形是中心对称图形.
解:正三角形要想变成和正偶数边形有关的多边形,边数最少也应是6边形,而六边形的中心角是60°,
所以至少旋转60°角后,两张图案构成的图形是中心对称图形.
答案:60.
16.(2020?台州)_??¨???????¤§??????_形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为 (a+b) .(用含a,b的代数式表示)【来源:21cnj*y.co*m】
解:如图,连接DK,DN,
∵∠KDN=∠MDT=90°,
∴∠KDM=∠NDT,
∵DK=DN,∠DKM=∠DNT=45°,
∴△DKM≌△DNT(ASA),
∴S△DKM=S△DNT,
∴S四边形DMNT=S△DKN=a,
∴正方形ABCD的面积=4×a+b=a+b.
答案:(a+b).
三、解答题
17.(2021?道里三模)如图,网格中的每个小正方形的边长均为1.点A、点B和点C在小正方形的顶点上.
(1)在图中确定点D,点D在小正方形的顶点上,连接DC,DA,使得到的四边形ABCD为中心对称图形;
(2)在(1)确定点D后,在_???????????????E_,点E(不与点C重合)在小正方形的顶点上,连接ED,EB得到凸四边形ABED,使∠EBA=∠EDA,直接写出ED的长.
解:(1)如图:
此时,由勾股定理得:CD=AB=2,AD=BC=.
∴四边形ABCD是平行四边形.
∴四边形ABCD是中心对称图形.
(2)如上图,此时∠EBA=45°,
∵AD?=AE?=1?+2?=5,DE?=1?+3?=10.
∴AD?+AE?=DE?.
∴△ADE是等腰直角三角形.
∠EDA=45°.
∴∠EDA=∠EBA.
ED=.
18.(2020?达州)如图,△ABC中,BC=2AB,D、E分别是边BC、AC的中点.将△CDE绕点E旋转180度,得△AFE.
(1)判断四边形ABDF的形状,并证明;
(2)已知AB=3,AD+BF=8,求四边形ABDF的面积S.
解:(1)结论:四边形ABDF是菱形.
∵CD=DB,CE=EA,
∴DE∥AB,AB=2DE,
由旋转的性质可知,DE=EF,
∴AB=DF,AB∥DF,
∴四边形ABDF是平行四边形,
∵BC=2AB,BD=DC,
∴BA=BD,
∴平行四边形ABDF是菱形.
(2)连接BF,AD交于点O.
∵四边形ABDF是菱形,
∴AD⊥BF,OB=OF,AO=OD,设OA=x,OB=y,
则有,
∴x+y=4,
∴x2+2xy+y2=16,
∴2xy=7,
∴S菱形ABDF=×BF×AD=2xy=7.
19.(2021?平江模拟)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
20.(2021?无锡模拟)如_???????????????O_ABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.21*cnjy*com
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方_???BDEF???_对称中心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
解:(1)结论:AD=CF.
理由:连接AD,CF.
∵四边形ABCO和四边形BDEF都是正方形,
∴AB=BC,BD=BF,∠ABC=∠FBD=90°,
∴∠ABD=∠FBD,
∴△ABD≌△CBF(SAS),
∴AD=CF.
(2)结论:点G的位置不发生变化.
理由:过点F作FH⊥CB交CB的延长线于点H.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠BFH=90°,
∴∠CBD=∠BFH,
∵BD=BF,
∴△BCD≌△FHB(AAS),
∴CD=BH=m﹣2,BC=FH=2,
∴F(4,﹣m),
又D(m,0),
∴M(2+,﹣),
作MN⊥x轴,在△CMN中,MN=,CN=,
∴△CMN是等腰直角三角形,
∴△OCG也是等腰直角三角形,
∴OG=OC=2,
∴G(0,2).
_21?????????è?????(www.21cnjy.com)_
23.2 中心对称 高频易错必刷题汇编
一、选择题
1.(2021?徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
2.(2021?广元)下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )
A.医疗废物 B.中国红十字会
C.医疗卫生服务机构 D.国际急救
3.(2021?大连模拟)在平面直角坐标系中,点P,Q的坐标分别为(2,﹣3),(2,3),则点P与点Q( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=1对称
4.(2021?青岛_????¨?????????????_△ABC的3个顶点都在格点上,将△ABC先向左平移4个单位长度,再作关于原点O的中心对称图形,得到△A′B′C′,则点A的对应点A′的坐标是( )21教育网
A.(﹣3,﹣2) B.(﹣3,2) C.(2,﹣2) D.(3,﹣2)
5.(2021?淮安模拟)若点A(1+m,1﹣n)与点B(﹣3,2)关于原点对称,则m+n的值为( )
A.﹣1 B.2 C.3 D.5
6.(2021?宁波模拟)两_?????¨????????????_(非正方形)纸片按如图呈中心对称方式放置在一个大正方形内,记重叠部分为①,不重叠部分为②和③;若已知正方形面积,且图形①和图形③相似,则下列可求的是( )
A.矩形的面积 B.矩形的周长
C.图形①的面积 D.图形②的面积
7.(2021?长沙模拟)若点A(a+b,1)与点B(﹣5,a﹣b)关于原点对称,则点P(a,b)的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,﹣3) D.(﹣3,2)
8.(2020?市南二模)_??¨???é???????±???_点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(6,50°)或P(6,﹣310°)或P(6,410°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(6,﹣490°) B.Q(6,590°) C.Q(6,﹣110°) D.Q(6,230°)
9.(2021?_???????¨??????????_面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2020A2021B2021(n是正整数)的顶点A2021的坐标是( )21cnjy.com
A.(4041,) B.(4041,﹣) C.(4043,) D.(4043,﹣)
10.(2021?安_?????????????????¨_菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )www.21-cn-jy.com
A.3+ B.2+2 C.2+ D.1+2
二、填空题
11.(2020?西城模拟)请写出一个是中心对称图形而不是轴对称图形的多边形,它的名字可以是 .
12.(2021?临沂)在平面_???è§?????????????_,平行四边形ABCD的对称中心是坐标原点,顶点A、B的坐标分别是(﹣1,1)、(2,1),将平行四边形ABCD沿x轴向右平移3个单位长度,则顶点C的对应点C1的坐标是 .
13.(2021?淮_??¨?¨???????è§????_以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣2,3)]等于 .21·世纪*教育网
14.(2020_?????°????????????_,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(﹣1,1),C(3,1).△A'B'C′是△ABC关于x轴的对称图形,将△A'B'C'绕点B'逆时针旋转180°,点A'的对应点为M,则点M的坐标为 .www-2-1-cnjy-com
15.(2020?九_?±?????¨??????????_,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 °的角后,两张硬纸片所构成的图形是中心对称图形.
16.(2020?台州)用_???????¤§?????????_地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为 .(用含a,b的代数式表示)2-1-c-n-j-y
三、解答题
17.(2021?道里三模)如图,网格中的每个小正方形的边长均为1.点A、点B和点C在小正方形的顶点上.
(1)在图中确定点D,点D在小正方形的顶点上,连接DC,DA,使得到的四边形ABCD为中心对称图形;
(2)在(1)确定点D后,在_???????????????E_,点E(不与点C重合)在小正方形的顶点上,连接ED,EB得到凸四边形ABED,使∠EBA=∠EDA,直接写出ED的长.21教育名师原创作品
18.(2020?达州)如图,△ABC中,BC=2AB,D、E分别是边BC、AC的中点.将△CDE绕点E旋转180度,得△AFE.
(1)判断四边形ABDF的形状,并证明;
(2)已知AB=3,AD+BF=8,求四边形ABDF的面积S.
19.(2021?平江模拟)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
20.(2021?_???é???¨??????????_图,正方形OABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.【版权所有:21教育】
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方形BD_EF???????§°???_心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
23.2 中心对称 高频易错必刷题汇编
一、选择题
1.(2021?徐州)下列图形,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
解:A.不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.是轴对称图形,也是中心对称图形,故此选项不符合题意;
C.不是轴对称图形,是中心对称图形,故此选项不符合题意;
D.是轴对称图形,不是中心对称图形,故此选项符合题意.
答案:D.
2.(2021?广元)下列图形均表示医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是( )
A.医疗废物 B.中国红十字会
C.医疗卫生服务机构 D.国际急救
解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.既是轴对称图形又是中心对称图形,故此选项符合题意;
D.不是轴对称图形,也不是中心对称图形,故此选项不合题意.
答案:C.
3.(2021?大连模拟)在平面直角坐标系中,点P,Q的坐标分别为(2,﹣3),(2,3),则点P与点Q( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=1对称
解:因为点P(2,﹣3)与点Q(2,3)的横坐标相同,纵坐标互为相反数,
所以点P(2,﹣3)与点Q(2,3)关于x轴对称.
答案:A.
4.(2021?青岛二模)如图,_???ABC???3_个顶点都在格点上,将△ABC先向左平移4个单位长度,再作关于原点O的中心对称图形,得到△A′B′C′,则点A的对应点A′的坐标是( )
A.(﹣3,﹣2) B.(﹣3,2) C.(2,﹣2) D.(3,﹣2)
解:由题意可知A的坐标为A(1,2),
将△ABC先向左平移4个单位长度后点A的对应点坐标为(﹣3,2).
再作关于原点O的中心对称图形,得到△A′B′C′,则点A的对应点A′的坐标是(3,﹣2).
答案:D.
5.(2021?淮安模拟)若点A(1+m,1﹣n)与点B(﹣3,2)关于原点对称,则m+n的值为( )
A.﹣1 B.2 C.3 D.5
解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于原点对称,
∴1+m=3,1﹣n=﹣2,
解得:m=2,n=3,
则m+n的值为:2+3=5.
答案:D.
6.(2021?宁波模拟)两张_??¨???????????????_非正方形)纸片按如图呈中心对称方式放置在一个大正方形内,记重叠部分为①,不重叠部分为②和③;若已知正方形面积,且图形①和图形③相似,则下列可求的是( )
A.矩形的面积 B.矩形的周长
C.图形①的面积 D.图形②的面积
解:设正方形的边长为c,矩形的长,宽分别为a,b,则=,
化简得到,2a2﹣2b2=3ac﹣3bc,即2(a﹣b)(a+b)=3c(a﹣b),
∵a≠b,
∴2(a+b)=3c,
即矩形的周长为3c,
答案:B.
7.(2021?长沙模拟)若点A(a+b,1)与点B(﹣5,a﹣b)关于原点对称,则点P(a,b)的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,﹣3) D.(﹣3,2)
解:∵点A(a+b,1)与点B(﹣5,a﹣b)关于原点对称,
∴,
解得:,
故点P(a,b)的坐标是(2,3).
答案:A.
8.(202_0?????????????¨?_)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(6,50°)或P(6,﹣310°)或P(6,410°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(6,﹣490°) B.Q(6,590°) C.Q(6,﹣110°) D.Q(6,230°)
解:∵P(6,50°)或P(6,﹣310°)或P(6,410°),
∴由点P关于点O成中心对称的点Q可得:点Q的极坐标为(6,230°),(6,﹣490°),(6,590°),
答案:C.
9.(2021?河南模拟)平_é?????è§??????????_中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2020A2021B2021(n是正整数)的顶点A2021的坐标是( )21·cn·jy·com
A.(4041,) B.(4041,﹣) C.(4043,) D.(4043,﹣)
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为:(1,),B1的坐标为:(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣=﹣,
∴点A2的坐标是:(3,﹣),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣)=,
∴点A3的坐标是:(5,),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣=﹣,
∴点A4的坐标是:(7,﹣),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×4﹣1,…,
∴An的横坐标是:2n﹣1,A2n+1的横坐标是:2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是:,当n为偶数时,An的纵坐标是:﹣,
∴顶点A2n+1的纵坐标是:,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是:(4n+1,),
∴△B2020A2021B2021的顶点A2021的横坐标是:4×1010+1=4041,纵坐标是:,2·1·c·n·j·y
答案:A.
10.(2021?_??????????????????_在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )21*cnjy*com
A.3+ B.2+2 C.2+ D.1+2
解:如图,连接BD,AC.
∵四边形ABCD是菱形,∠BAD=120°,
∴AB=BC=CD=AD=2,∠BAO=∠DAO=60°,BD⊥AC,
∴∠ABO=∠CBO=30°,
∴OA=AB=1,OB=OA=,
∵OE⊥AB,OF⊥BC,
∴∠BEO=∠BFO=90°,
在△BEO和△BFO中,
,
∴△BEO≌△BFO(AAS),
∴OE=OF,BE=BF,
∵∠EBF=60°,
∴△BEF是等边三角形,
∴EF=BE=×=,
同法可证,△DGH,△OEH,△OFG都是等边三角形,
∴EF=GH=,EH=FG=,
∴四边形EFGH的周长=3+,
答案:A.
二、填空题
11.(2020?西城模拟)请写出一个是中心对称图形而不是轴对称图形的多边形,它的名字可以是 平行四边形.(答案不唯一) .21世纪教育网版权所有
解:由平行四边形的性质可知,平行四边形是中心对称图形而不是轴对称图形.
答案:平行四边形(答案不唯一).
12.(2021?临_????????¨???é?????_角坐标系中,平行四边形ABCD的对称中心是坐标原点,顶点A、B的坐标分别是(﹣1,1)、(2,1),将平行四边形ABCD沿x轴向右平移3个单位长度,则顶点C的对应点C1的坐标是 (4,﹣1) .【来源:21·世纪·教育·网】
解:∵平行四边形ABCD的对称中心是坐标原点,
∴点A,点C关于原点对称,
∵A(﹣1,1),
∴C(1,﹣1),
∴将平行四边形ABCD沿x轴向右平移3个单位长度,则顶点C的对应点C1的坐标是(4,﹣1),
答案:(4,﹣1).
13.(20_21????·???¨?¨?_拟)规定以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣2,3)]等于 (2,3) .【出处:21教育名师】
解:∵①f(m,n)=(m,﹣n),②g(m,n)=(﹣m,﹣n),
∴g[f(﹣2,3)]=g(﹣2,﹣3)=(2,3).
答案:(2,3).
14.(2020?泰安)_??????????°???????_形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(﹣1,1),C(3,1).△A'B'C′是△ABC关于x轴的对称图形,将△A'B'C'绕点B'逆时针旋转180°,点A'的对应点为M,则点M的坐标为 (﹣2,1) .
解:将△A'B'C'绕点B'逆时针旋转180°,如图所示:
所以点M的坐标为(﹣2,1),
答案:(﹣2,1).
15.(2020?九江一模)如图_?????¤????????¨é??_合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转 60 °的角后,两张硬纸片所构成的图形是中心对称图形.
解:正三角形要想变成和正偶数边形有关的多边形,边数最少也应是6边形,而六边形的中心角是60°,
所以至少旋转60°角后,两张图案构成的图形是中心对称图形.
答案:60.
16.(2020?台州)_??¨???????¤§??????_形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为 (a+b) .(用含a,b的代数式表示)【来源:21cnj*y.co*m】
解:如图,连接DK,DN,
∵∠KDN=∠MDT=90°,
∴∠KDM=∠NDT,
∵DK=DN,∠DKM=∠DNT=45°,
∴△DKM≌△DNT(ASA),
∴S△DKM=S△DNT,
∴S四边形DMNT=S△DKN=a,
∴正方形ABCD的面积=4×a+b=a+b.
答案:(a+b).
三、解答题
17.(2021?道里三模)如图,网格中的每个小正方形的边长均为1.点A、点B和点C在小正方形的顶点上.
(1)在图中确定点D,点D在小正方形的顶点上,连接DC,DA,使得到的四边形ABCD为中心对称图形;
(2)在(1)确定点D后,在_???????????????E_,点E(不与点C重合)在小正方形的顶点上,连接ED,EB得到凸四边形ABED,使∠EBA=∠EDA,直接写出ED的长.
解:(1)如图:
此时,由勾股定理得:CD=AB=2,AD=BC=.
∴四边形ABCD是平行四边形.
∴四边形ABCD是中心对称图形.
(2)如上图,此时∠EBA=45°,
∵AD?=AE?=1?+2?=5,DE?=1?+3?=10.
∴AD?+AE?=DE?.
∴△ADE是等腰直角三角形.
∠EDA=45°.
∴∠EDA=∠EBA.
ED=.
18.(2020?达州)如图,△ABC中,BC=2AB,D、E分别是边BC、AC的中点.将△CDE绕点E旋转180度,得△AFE.
(1)判断四边形ABDF的形状,并证明;
(2)已知AB=3,AD+BF=8,求四边形ABDF的面积S.
解:(1)结论:四边形ABDF是菱形.
∵CD=DB,CE=EA,
∴DE∥AB,AB=2DE,
由旋转的性质可知,DE=EF,
∴AB=DF,AB∥DF,
∴四边形ABDF是平行四边形,
∵BC=2AB,BD=DC,
∴BA=BD,
∴平行四边形ABDF是菱形.
(2)连接BF,AD交于点O.
∵四边形ABDF是菱形,
∴AD⊥BF,OB=OF,AO=OD,设OA=x,OB=y,
则有,
∴x+y=4,
∴x2+2xy+y2=16,
∴2xy=7,
∴S菱形ABDF=×BF×AD=2xy=7.
19.(2021?平江模拟)如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
20.(2021?无锡模拟)如_???????????????O_ABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.21*cnjy*com
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方_???BDEF???_对称中心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
解:(1)结论:AD=CF.
理由:连接AD,CF.
∵四边形ABCO和四边形BDEF都是正方形,
∴AB=BC,BD=BF,∠ABC=∠FBD=90°,
∴∠ABD=∠FBD,
∴△ABD≌△CBF(SAS),
∴AD=CF.
(2)结论:点G的位置不发生变化.
理由:过点F作FH⊥CB交CB的延长线于点H.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠BFH=90°,
∴∠CBD=∠BFH,
∵BD=BF,
∴△BCD≌△FHB(AAS),
∴CD=BH=m﹣2,BC=FH=2,
∴F(4,﹣m),
又D(m,0),
∴M(2+,﹣),
作MN⊥x轴,在△CMN中,MN=,CN=,
∴△CMN是等腰直角三角形,
∴△OCG也是等腰直角三角形,
∴OG=OC=2,
∴G(0,2).
_21?????????è?????(www.21cnjy.com)_
同课章节目录
