七年级数学三角形中位线

(共26张PPT)
达县沿河乡中心学校 谯勉华
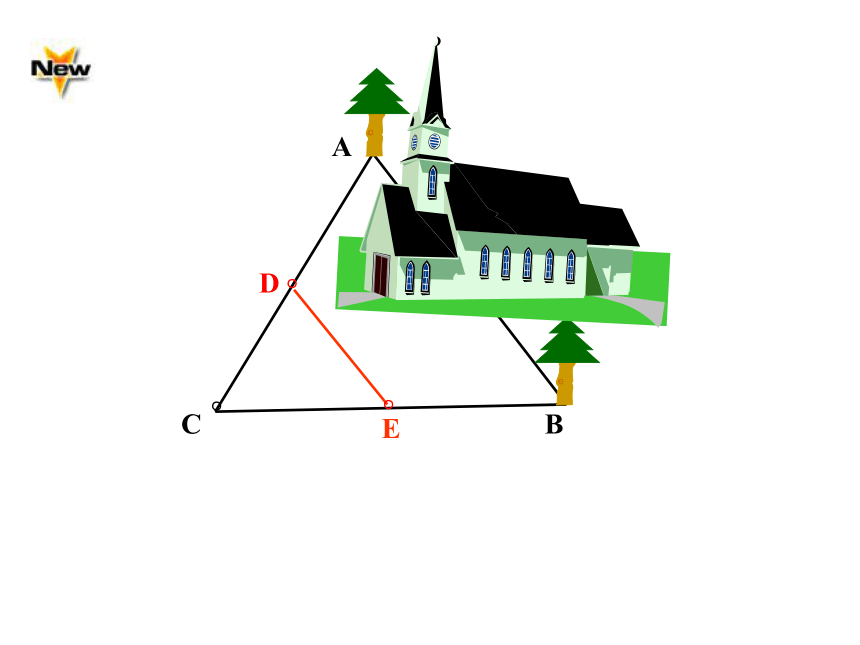
如图，A、B两棵树被一座高大建筑物隔开，现在要测量出A、B两树间的距离 ，但又无法直接去测量，请问该怎么办呢？
A
B
。
。
A
B
。
。
C
。
D
。
E
。
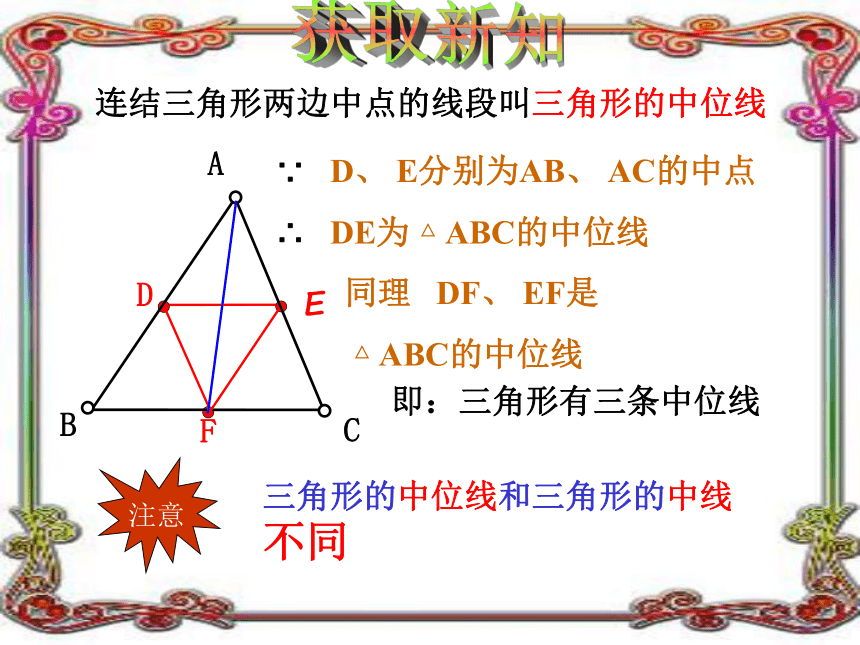
连结三角形两边中点的线段叫三角形的中位线
即：三角形有三条中位线
∵ D、 E分别为AB、 AC的中点
∴ DE为 △ ABC的中位线
三角形的中位线和三角形的中线不同
注意
同理 DF、 EF是
△ ABC的中位线
E
D
F
A
C
B
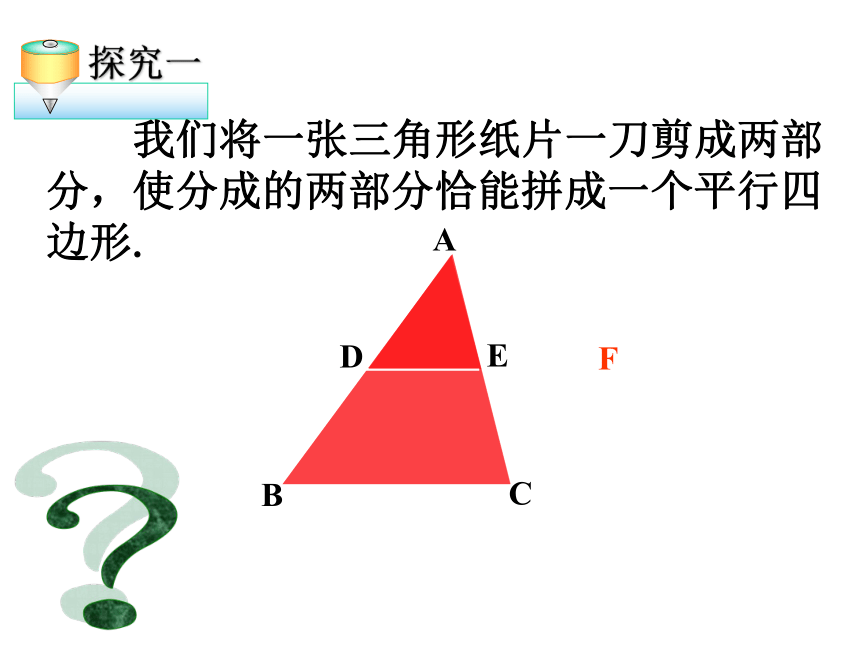
我们将一张三角形纸片一刀剪成两部分，使分成的两部分恰能拼成一个平行四边形.
A
B
C
D
E
F
探究一
A
B
C
D
E
F
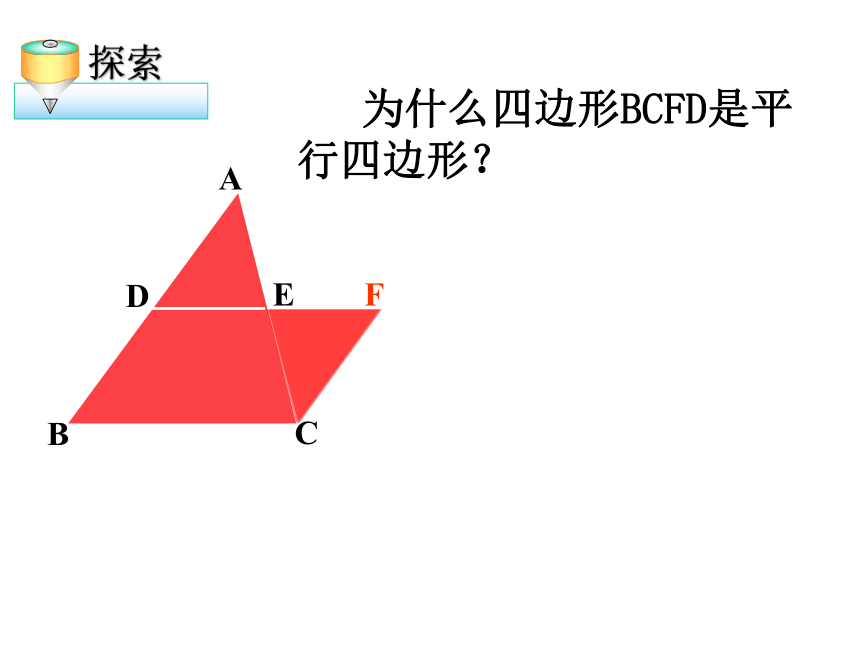
为什么四边形BCFD是平行四边形？
探索
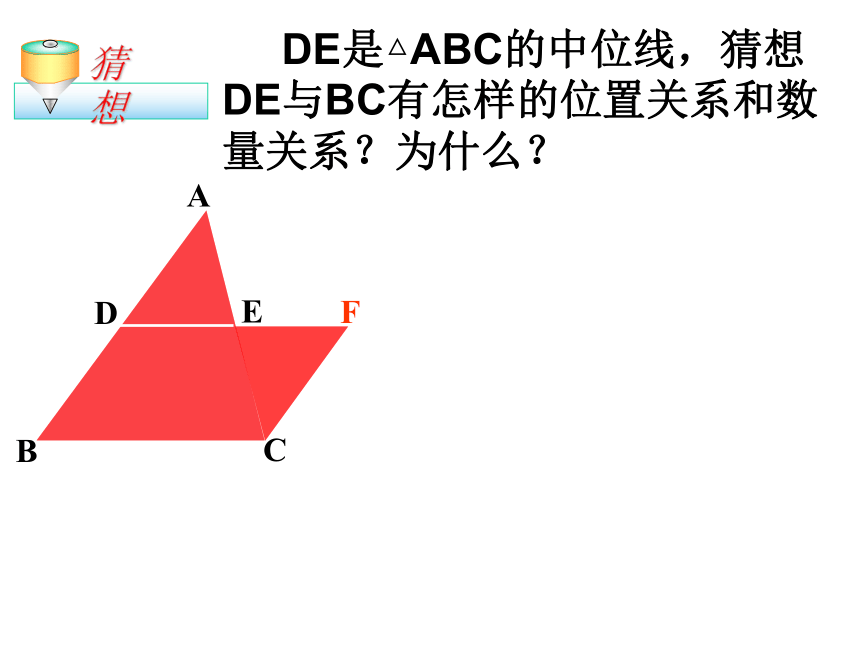
DE是△ABC的中位线，猜想DE与BC有怎样的位置关系和数量关系？为什么？
猜 想
A
B
C
D
E
F
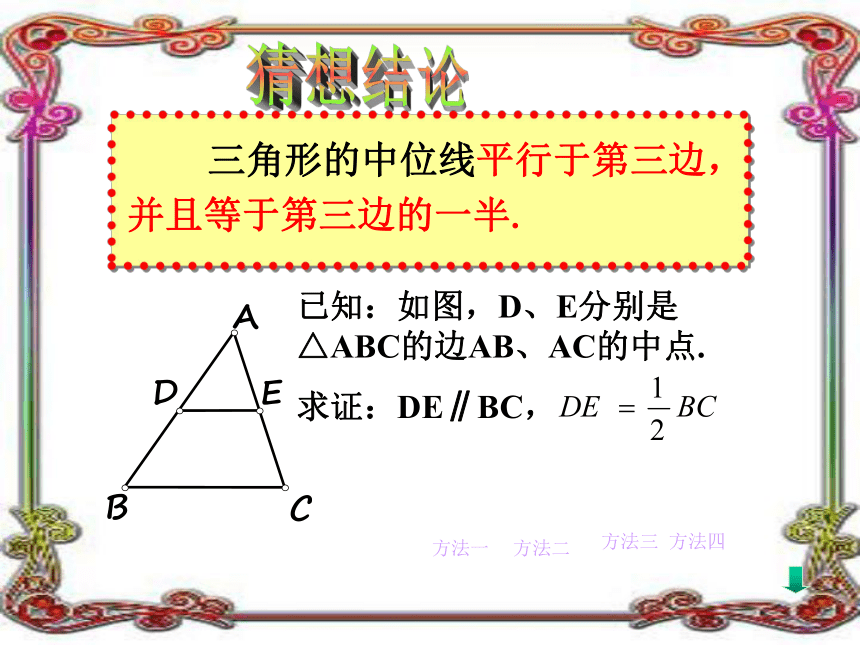
　　三角形的中位线平行于第三边，并且等于第三边的一半.
已知：如图，D、E分别是△ABC的边AB、AC的中点.
求证：DE∥BC，
方法二
方法三
方法一
C
E
D
B
A
方法四
C
E
D
F
B
A
返回
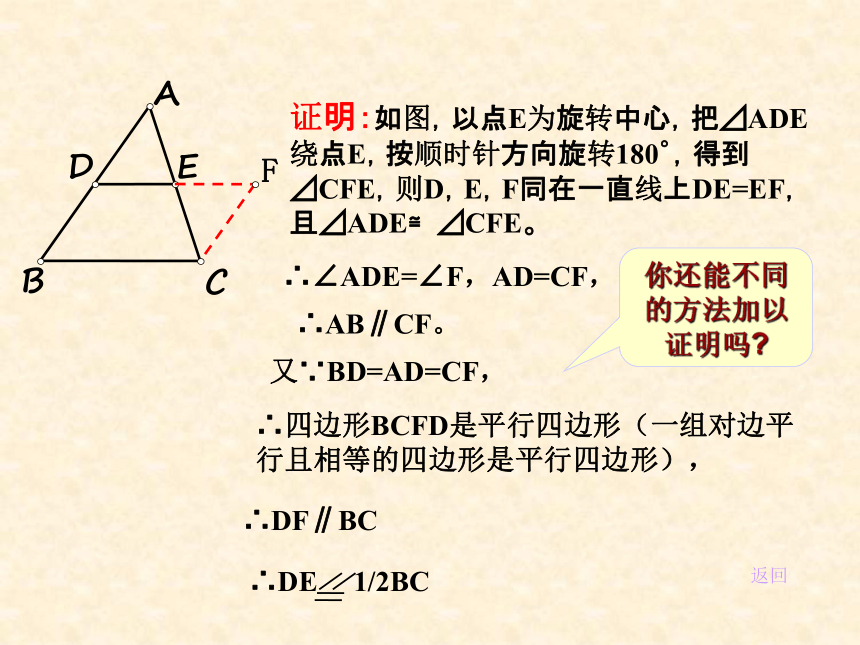
你还能不同的方法加以证明吗
证明：如图，以点E为旋转中心，把⊿ADE绕点E，按顺时针方向旋转180゜，得到⊿CFE，则D，E，F同在一直线上DE=EF，且⊿ADE≌⊿CFE。
∴∠ADE=∠F，AD=CF，
∴AB∥CF。
又∵BD=AD=CF，
∴四边形BCFD是平行四边形（一组对边平行且相等的四边形是平行四边形），
∴DF∥BC
∴DE 1/2BC
C
E
D
F
B
A
证法二：过点C作AB的平行线交DE的延长线于F
∵CF∥AB，
∴∠A=∠ECF
又AE=EC，∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD，
∴DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF=1/2BC
返回
A
B
C
E
D
F
证法三：如图，延长DE至F,
使EF=DE，
连接CD、AF、CF
∵AE=EC
∴DE=EF
∴四边形ADCF是平行四边形∴AD FC
又D为AB中点，
∴DB FC
∴四边形BCFD是平行四边形
∴DE// BC 且DE=EF=1/2BC
返回
A
C
E
D
F
G
B
证法四：如图，过E作AB的平行线交BC于F，自A作BC的平行线交FE于G
∵AG∥BC∴∠EAG=∠ECF
又∵ AE=EC, ∠AEG=∠CEF
∴△AEG≌△CEF∴AG=FC，GE=EF
又AB∥GF，AG∥BF∴四边形ABFG是平行四边形
∴BF=AG=FC，AB=GF
又D为AB中点，E为GF中点，
∴DB EF
∴四边形DBFE是平行四边形
∴DE∥BF，即DE∥BC，DE=BF=FC
即DE=1/2BC
返回
　　三角形的中位线平行于第三边，并且等于第三边的一半.
几何语言：
∵DE是△ABC的中位线 ∵ AD=BD,AE=CE
∴DE∥BC,且DE=1/2BC ∴DE∥BC,且 DE=1/2BC
C
E
D
B
A
画出△ABC中所有的中位线
B
D
A
E
C
F
三条中位线围成一个新的三角形，它与原来的三角形有无关系 哪方面有关系
(1) △DEF的周长与 △ABC的周长有什么关系
(2) △DEF的面积与 △ABC的面积有什么关系
４个小的三角形之间有什么关系
热身练习:
(3)若∠B=40O ，则∠EFD=______
A
B
C
E
F
D
如图，已知△ABC，D、E、F分别是BC、AB、AC边上的中点。
(1)若△ABC的周长为18cm，它的三条中位线围成的△DEF的周长是________
400
9cm
(2)图中有_____个平行四边形
3
如图，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G．
求证：　
证明 :连结ED，
∵　D、E分别是边BC、AB的中点，
∴　DE∥AC，
（三角形的中位线平行于第三边并且等于第三边的一半），
∴　△ACG∽△DEG，
∴
∴
如果在图1中，取AC的中点F，假设BF与AD交于G′，如图2，那么我们
同理有 ，所以
有 ，即两图中的点G与G′是重合的．
三角形三条边上的中线交于一点，这个点就是三角形的重心，重心与一边中点的连线
的长是对应中线长的
．
猜一猜：画一个任意四边形，并画出四边的中点，再顺次连接四边形的中点，得到的四边形的形状是什么？
已知：如图，在四边形ABCD中，E、F、G、H分别是 AB、BC、CD、DA的中点.
求证：四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
从例题中你能得到什么结论？
顺次连接四边形各边中点的线段组成一个
平行四边形
A
B
C
D
E
F
G
H
1、如图,DE是△ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.
F
E
D
C
B
A
O
作业题
2.已知: 如图,DE,EF是⊿ABC的两条中位线.求证:四边形BFED是平行四边形.
D
B
C
F
E
A
(第3题)
作业题
3.已知: 如图,在RT△ABC中，∠ACB=90°，CD是斜边AB的中线，MN是中位线。求证：CD=MN
作业题
B
A
C
D
M
N
4 、已知：如图，△ABC是锐角三角形。分别以AB，AC为边向外侧作等边三角形ABM和等边三角形CAN。D，E，F分别是MB，BC，CN的中点，连结DE，EF。
A
B
C
D
E
F
N
M
求证：DE=EF
作业题