1 4 1空间向量与平行、垂直关系 课件 19张-2021-2022学年吉林省白山市抚松县第一中学高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1 4 1空间向量与平行、垂直关系 课件 19张-2021-2022学年吉林省白山市抚松县第一中学高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 20:27:42 | ||
图片预览


文档简介
1、理解直线的方向向量和平面的法向量,会用待定系数法求平面的法向量;
2、能用向量方法判定空间线面的平行和垂直关系。
研究
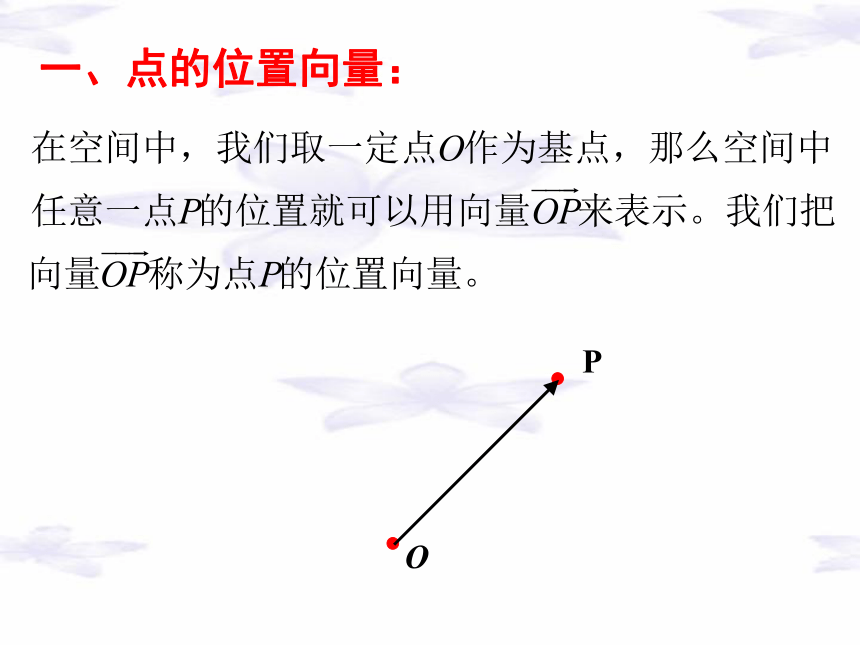
O
P
一、点的位置向量:
A
B
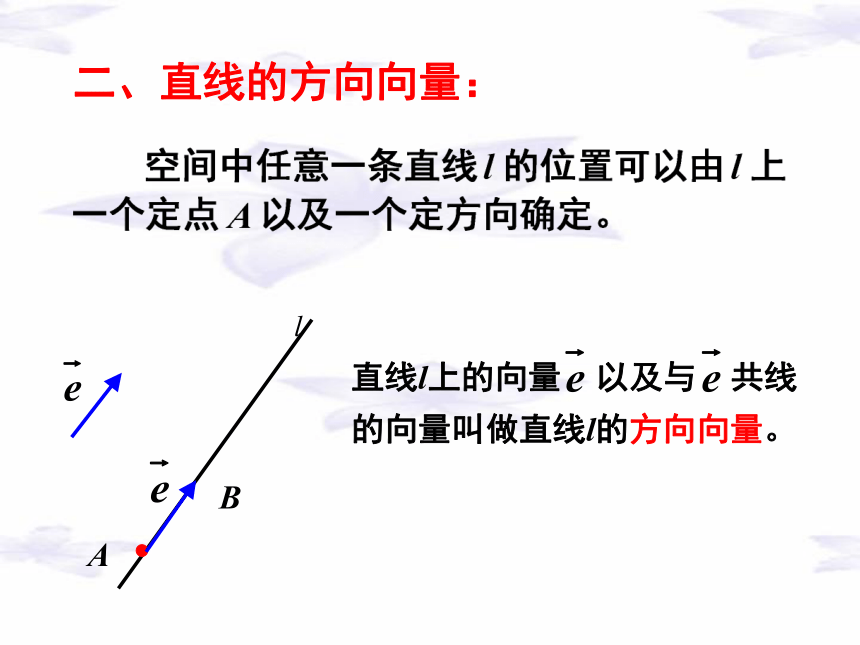
直线l上的向量 以及与 共线的向量叫做直线l的方向向量。
二、直线的方向向量:
P
O
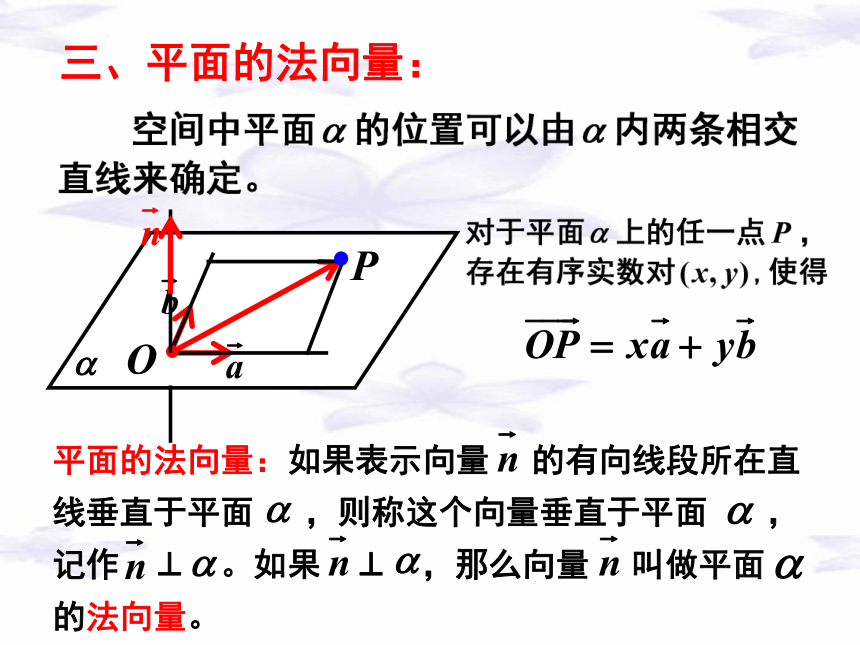
三、平面的法向量:
平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ 。如果 ⊥ ,那么向量 叫做平面 的法向量。
l
A
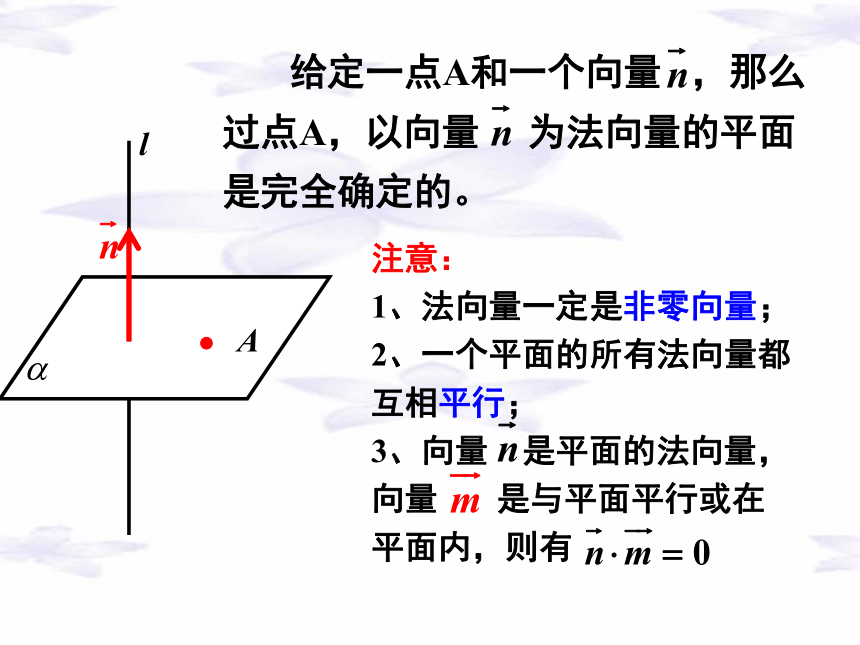
给定一点A和一个向量 ,那么过点A,以向量 为法向量的平面是完全确定的。
注意:
1、法向量一定是非零向量;
2、一个平面的所有法向量都互相平行;
3、向量 是平面的法向量,向量 是与平面平行或在平面内,则有
因为方向向量与法向量可以确定直线和平面的位置,所以可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系。
那么如何用直线的方向向量表示空间两直线平行、垂直的位置关系呢?
如何用平面的法向量表示空间两平面平行、垂直的位置关系呢?
l1
l2
l1
四、平行关系:
线面平行:
线线平行:
面面平行:
l1
l2
l1
五、垂直关系:
线线垂直:
线面垂直:
面面垂直:
【总一总★成竹在胸】
一、点的位置向量:
二、直线的方向向量:
三、平面的法向量:
四、平行关系:
五、垂直关系:
2、能用向量方法判定空间线面的平行和垂直关系。
研究
O
P
一、点的位置向量:
A
B
直线l上的向量 以及与 共线的向量叫做直线l的方向向量。
二、直线的方向向量:
P
O
三、平面的法向量:
平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ 。如果 ⊥ ,那么向量 叫做平面 的法向量。
l
A
给定一点A和一个向量 ,那么过点A,以向量 为法向量的平面是完全确定的。
注意:
1、法向量一定是非零向量;
2、一个平面的所有法向量都互相平行;
3、向量 是平面的法向量,向量 是与平面平行或在平面内,则有
因为方向向量与法向量可以确定直线和平面的位置,所以可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系。
那么如何用直线的方向向量表示空间两直线平行、垂直的位置关系呢?
如何用平面的法向量表示空间两平面平行、垂直的位置关系呢?
l1
l2
l1
四、平行关系:
线面平行:
线线平行:
面面平行:
l1
l2
l1
五、垂直关系:
线线垂直:
线面垂直:
面面垂直:
【总一总★成竹在胸】
一、点的位置向量:
二、直线的方向向量:
三、平面的法向量:
四、平行关系:
五、垂直关系:
