2 5 2圆的切线方程 -2021-2022学年高二数学人教A版(2019)选择性必修第一册(16张PPT)
文档属性
| 名称 | 2 5 2圆的切线方程 -2021-2022学年高二数学人教A版(2019)选择性必修第一册(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 615.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览


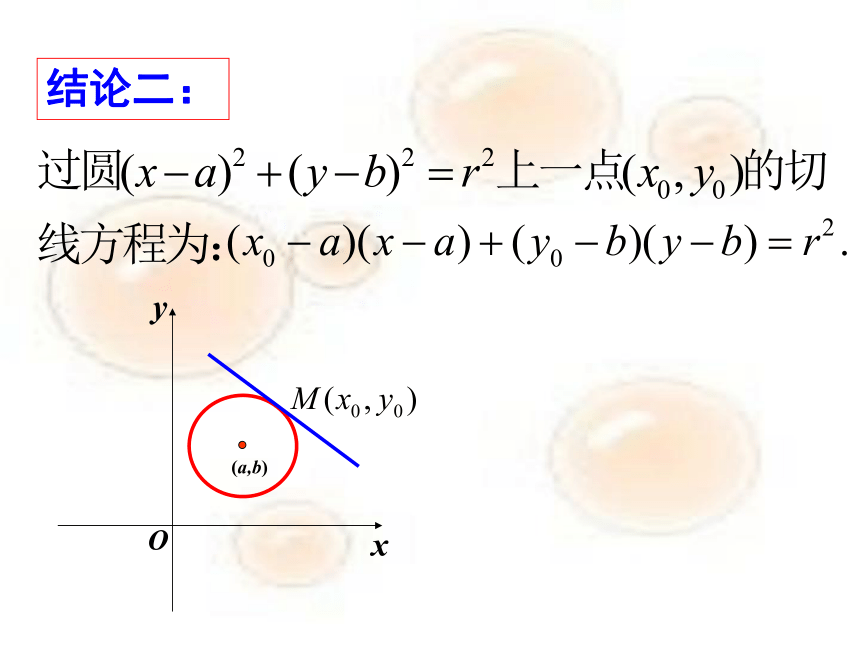
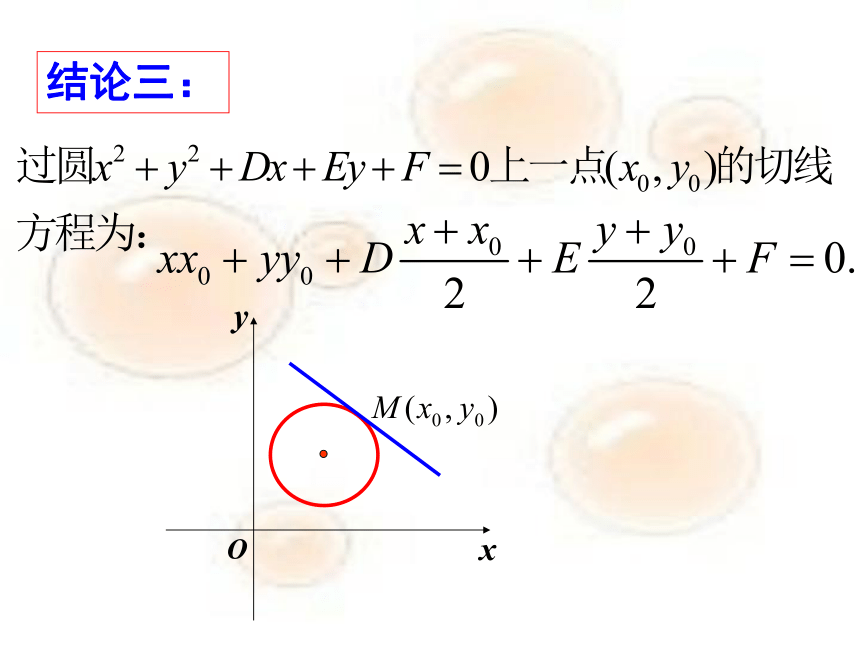

文档简介
掌握圆的切线方程的类型,及求切线方程的方法。
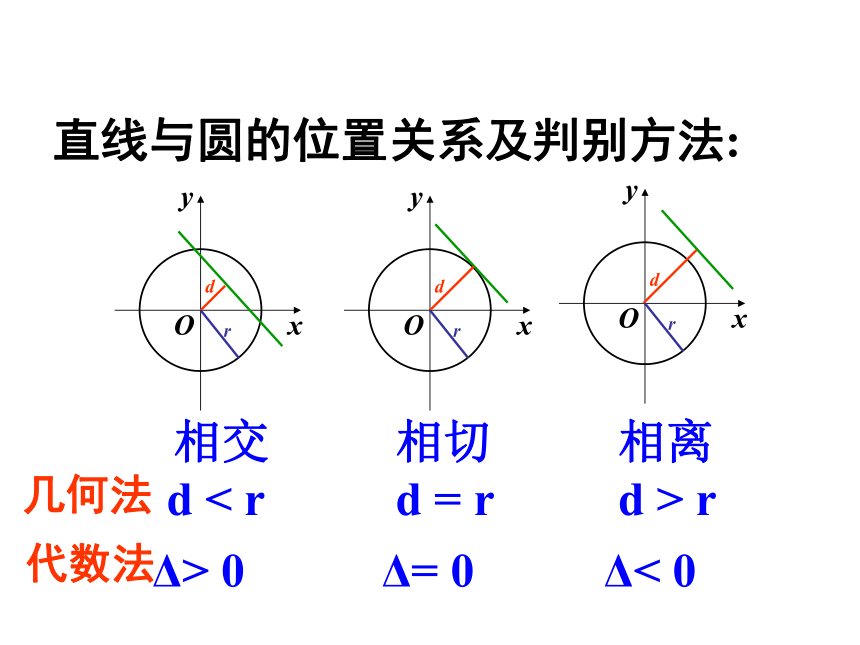
直线与圆的位置关系及判别方法:
d
r
x
y
O
d
r
x
y
O
d
r
x
y
O
相交
相切
相离
d < r
d = r
d > r
Δ> 0
Δ= 0
Δ< 0
几何法
代数法
圆的切线方程的几种基本类型:
1.过圆上一点的切线方程
2.过圆外一点的切线方程
3.已知斜率的切线方程
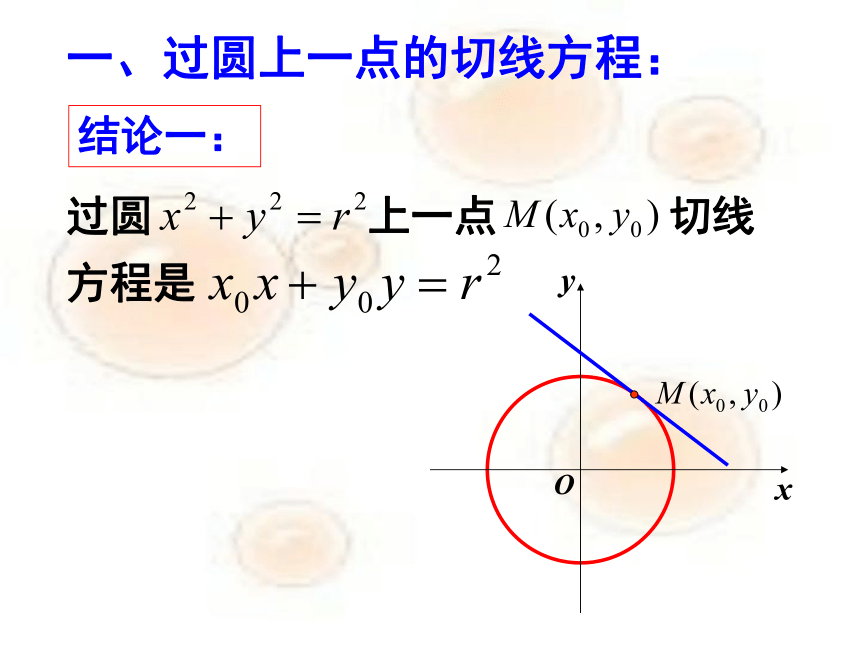
结论一:
过圆 上一点 切线方程是
y
x
O
一、过圆上一点的切线方程:
y
x
O
(a,b)
结论二:
y
x
O
结论三:
设切线方程为 y-yo= k(x-xo)
(1) 利用 _______________________________
待定 k;
(2) 利用 _______________________________
待定 k;
圆心到切线的距离等于圆半径
联立方程组消去一元后判别式等于零
注:此时切线一般有两条,故 k 有二解,
若只求出一解,需考虑 ___________
k 不存在
二、过圆外一点的切线方程:
三、已知斜率的切线方程:
o
x
A
B
y
已知直线L:y=x+b与曲线C:
有两个不同的公共点,求实数b的取值范围。
l2
l1
【总一总★成竹在胸】
圆上一点
圆外一点
圆的切线
斜率已知
结论1
结论2
结论3
几何法
代数法
应用
1、预习圆和圆有哪几种的位置关系;
2、预习圆和圆的位置关系的判定方法。
直线与圆的位置关系及判别方法:
d
r
x
y
O
d
r
x
y
O
d
r
x
y
O
相交
相切
相离
d < r
d = r
d > r
Δ> 0
Δ= 0
Δ< 0
几何法
代数法
圆的切线方程的几种基本类型:
1.过圆上一点的切线方程
2.过圆外一点的切线方程
3.已知斜率的切线方程
结论一:
过圆 上一点 切线方程是
y
x
O
一、过圆上一点的切线方程:
y
x
O
(a,b)
结论二:
y
x
O
结论三:
设切线方程为 y-yo= k(x-xo)
(1) 利用 _______________________________
待定 k;
(2) 利用 _______________________________
待定 k;
圆心到切线的距离等于圆半径
联立方程组消去一元后判别式等于零
注:此时切线一般有两条,故 k 有二解,
若只求出一解,需考虑 ___________
k 不存在
二、过圆外一点的切线方程:
三、已知斜率的切线方程:
o
x
A
B
y
已知直线L:y=x+b与曲线C:
有两个不同的公共点,求实数b的取值范围。
l2
l1
【总一总★成竹在胸】
圆上一点
圆外一点
圆的切线
斜率已知
结论1
结论2
结论3
几何法
代数法
应用
1、预习圆和圆有哪几种的位置关系;
2、预习圆和圆的位置关系的判定方法。
