2 5 3圆与圆的位置关系 -2021-2022学年高二数学人教A版(2019)选择性必修第一册(15张PPT)
文档属性
| 名称 | 2 5 3圆与圆的位置关系 -2021-2022学年高二数学人教A版(2019)选择性必修第一册(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 626.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览



文档简介
1、理解圆和圆的位置关系有哪几种位置及判定方法;
2、理解并掌握过交点的圆系方程。
1、点和圆的位置关系有几种?如何判定?
答:三种。点在圆外;点在圆上;点在圆内。
设点P(x0,y0),圆(x-a)2+(y-b)2=r2,
圆心(a,b)到P(x0,y0)的距离为d,则:
代数法:点在圆内?(x0 -a)2+(y0 -b)2<r2
点在圆上?(x0 -a)2+(y0 -b)2=r2
点在圆外?(x0 -a)2+(y0 -b)2>r2
几何法:点在圆内?d 点在圆上?d=r
点在圆外?d>r
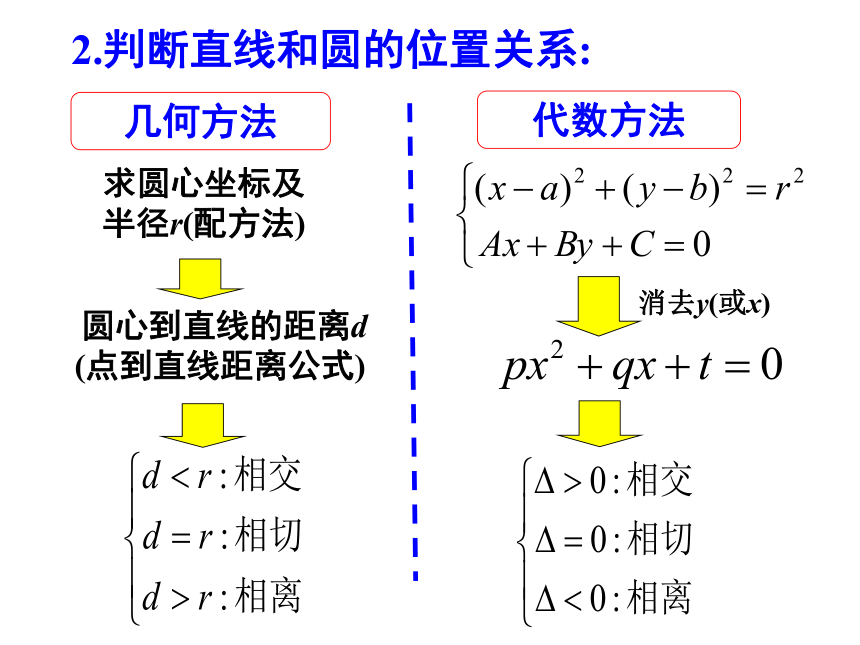
2.判断直线和圆的位置关系:
几何方法
求圆心坐标及
半径r(配方法)
圆心到直线的距离d
(点到直线距离公式)
代数方法
消去y(或x)
直线和圆的位置关系
几何方法
代数方法
圆和圆的位置关系
几何方法
代数方法
类比
猜想
?
O1
r1
?
O2
r2
d
?
O1
r1
?
O2
r2
d
?
O1
r1
?
O2
r2
d
?
O2
r2
d
?
O1
r1
?
r1
d
?
O2
r2
O1
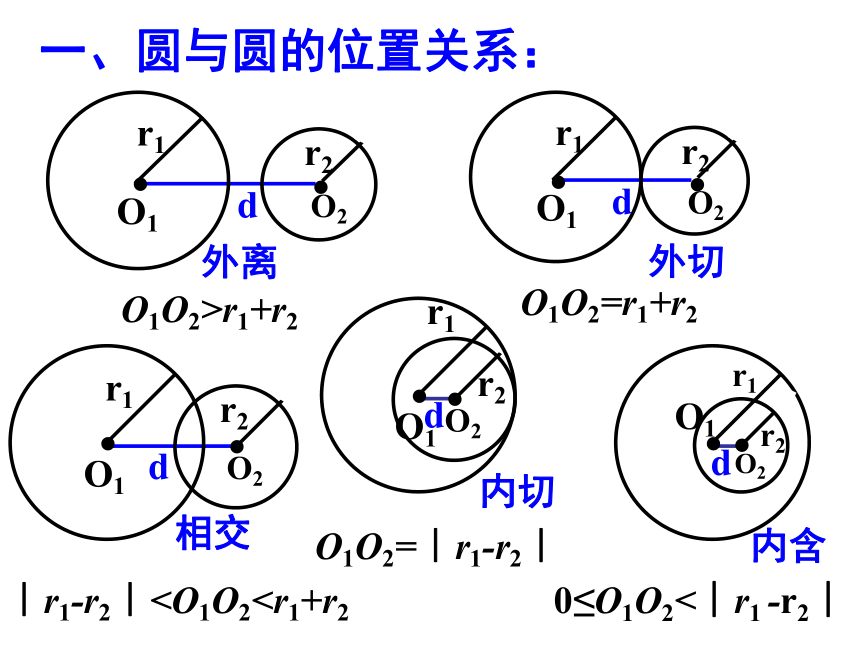
一、圆与圆的位置关系:
外离
O1O2>r1+r2
O1O2=r1+r2
外切
︱r1-r2︱相交
O1O2=︱r1-r2︱
内切
0≤O1O2<︱r1 -r2︱
内含
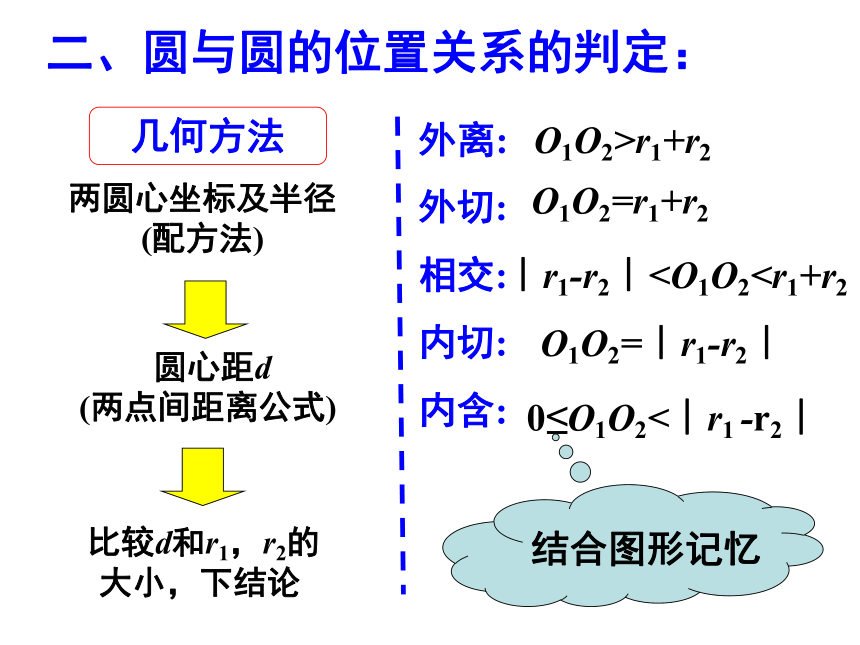
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
外离:
外切:
相交:
内切:
内含:
结合图形记忆
二、圆与圆的位置关系的判定:
O1O2>r1+r2
O1O2=r1+r2
︱r1-r2︱O1O2=︱r1-r2︱
0≤O1O2<︱r1 -r2︱
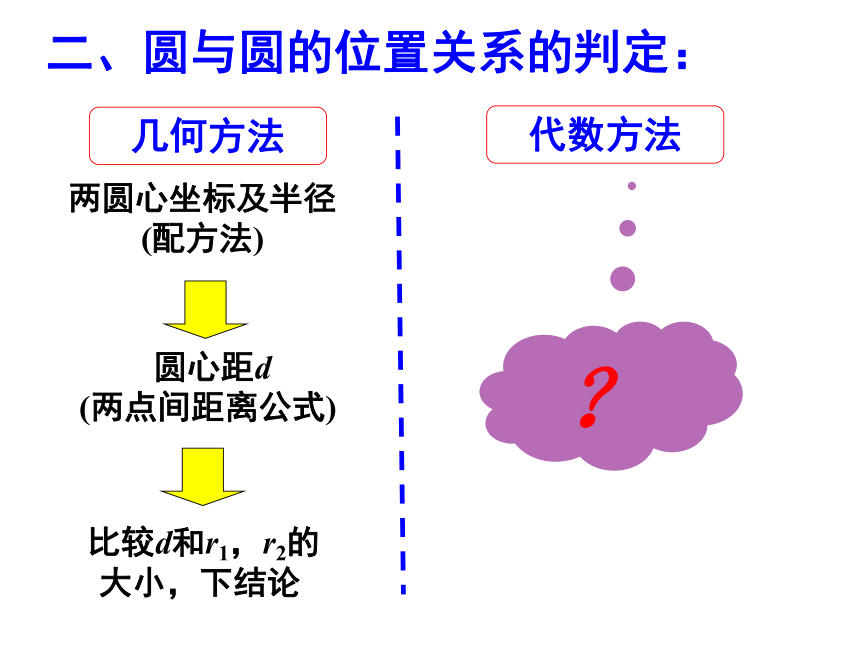
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
代数方法
?
判断C1和C2的位置关系:
解:联立两个方程组得
所以圆C1与圆C2有两个不同的A(x1,y1),B(x2,y2)
判断两圆位置关系
几何方法
代数方法
各有何优劣,如何选用?
(1)当Δ=0时,有一个交点,两圆位置关系如何?
内切或外切
(2)当Δ<0时,没有交点,两圆位置关系如何?
几何方法直观,但不能求出交点;
代数方法能求出交点,
但Δ=0,Δ<0时,不能判断圆的位置关系。
内含或外离
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
代数方法
消去y(或x)
三、共点圆系方程:
此圆系方程少一个圆C2
例1:求过两圆 x 2 + y 2 -4x + 2y = 0 和
x 2 + y 2 -2y -4 = 0 的交点,
解:设所求圆方程为
故所求圆方程为
圆心在直线 2x + 4y = 1上的圆方程。
例2:求两圆C1:x2+y 2-10x-10y=0 和
C2: x2+ y2+6x+2y- 40=0 的公共弦长。
解:
A
B
C2
C1
D
2、理解并掌握过交点的圆系方程。
1、点和圆的位置关系有几种?如何判定?
答:三种。点在圆外;点在圆上;点在圆内。
设点P(x0,y0),圆(x-a)2+(y-b)2=r2,
圆心(a,b)到P(x0,y0)的距离为d,则:
代数法:点在圆内?(x0 -a)2+(y0 -b)2<r2
点在圆上?(x0 -a)2+(y0 -b)2=r2
点在圆外?(x0 -a)2+(y0 -b)2>r2
几何法:点在圆内?d
点在圆外?d>r
2.判断直线和圆的位置关系:
几何方法
求圆心坐标及
半径r(配方法)
圆心到直线的距离d
(点到直线距离公式)
代数方法
消去y(或x)
直线和圆的位置关系
几何方法
代数方法
圆和圆的位置关系
几何方法
代数方法
类比
猜想
?
O1
r1
?
O2
r2
d
?
O1
r1
?
O2
r2
d
?
O1
r1
?
O2
r2
d
?
O2
r2
d
?
O1
r1
?
r1
d
?
O2
r2
O1
一、圆与圆的位置关系:
外离
O1O2>r1+r2
O1O2=r1+r2
外切
︱r1-r2︱
O1O2=︱r1-r2︱
内切
0≤O1O2<︱r1 -r2︱
内含
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
外离:
外切:
相交:
内切:
内含:
结合图形记忆
二、圆与圆的位置关系的判定:
O1O2>r1+r2
O1O2=r1+r2
︱r1-r2︱
0≤O1O2<︱r1 -r2︱
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
代数方法
?
判断C1和C2的位置关系:
解:联立两个方程组得
所以圆C1与圆C2有两个不同的A(x1,y1),B(x2,y2)
判断两圆位置关系
几何方法
代数方法
各有何优劣,如何选用?
(1)当Δ=0时,有一个交点,两圆位置关系如何?
内切或外切
(2)当Δ<0时,没有交点,两圆位置关系如何?
几何方法直观,但不能求出交点;
代数方法能求出交点,
但Δ=0,Δ<0时,不能判断圆的位置关系。
内含或外离
几何方法
两圆心坐标及半径
(配方法)
圆心距d
(两点间距离公式)
比较d和r1,r2的
大小,下结论
二、圆与圆的位置关系的判定:
代数方法
消去y(或x)
三、共点圆系方程:
此圆系方程少一个圆C2
例1:求过两圆 x 2 + y 2 -4x + 2y = 0 和
x 2 + y 2 -2y -4 = 0 的交点,
解:设所求圆方程为
故所求圆方程为
圆心在直线 2x + 4y = 1上的圆方程。
例2:求两圆C1:x2+y 2-10x-10y=0 和
C2: x2+ y2+6x+2y- 40=0 的公共弦长。
解:
A
B
C2
C1
D
