5 6函数y=Asin(ωx+φ)的图象 -2021-2022学年高一数学人教A版(2019)必修第一册(25张PPT)
文档属性
| 名称 | 5 6函数y=Asin(ωx+φ)的图象 -2021-2022学年高一数学人教A版(2019)必修第一册(25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 20:42:23 | ||
图片预览




文档简介
(1)y=sinx与y=sin(x+?)的图象关系;
(2)y=sinx与y=sin?x的图象关系;
(3)y=sinx与y=Asinx的图象关系;
(4)y=sinx与y=Asin(?x+?)的图象关系。
y
x
O
1
1
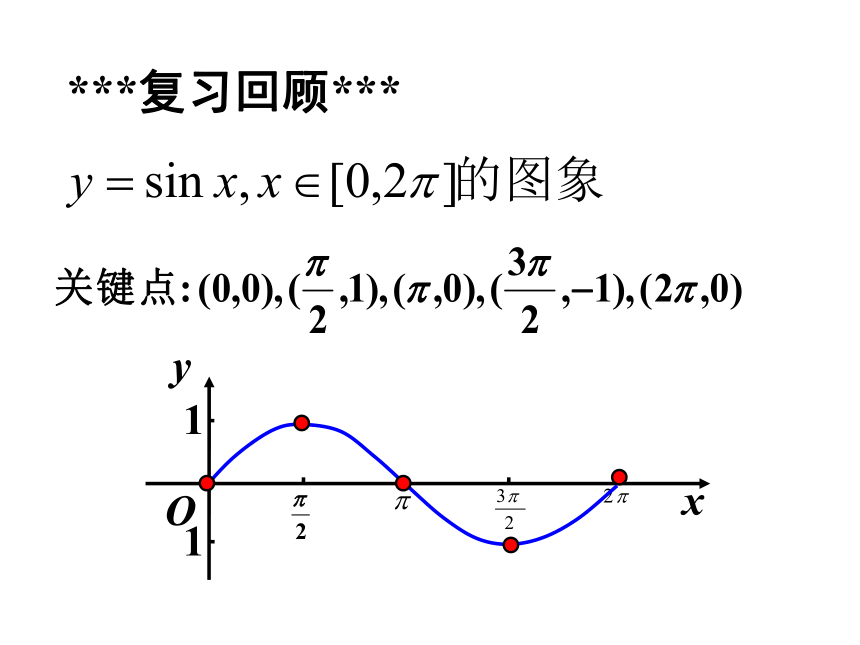
***复习回顾***
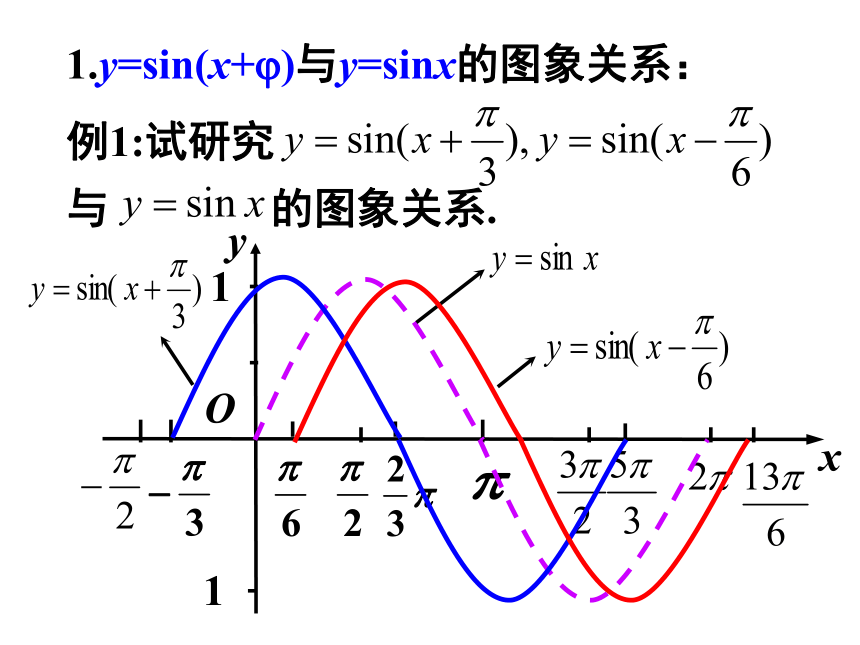
1.y=sin(x+?)与y=sinx的图象关系:
例1:试研究 与 的图象关系.
y
1
-1
O
x
所有的点向左(? >0)
或向右(? <0)平移
| ? | 个单位
一、函数y=sin(x+?)图象:
函数 y=sin(x+?)(??0) 的图象可以看作是把y=sinx 的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动|?|个单位而得到的.
y=sinx
y=sin(x+?)
?的变化引起图象位置发生变化(左加右减)
平移变换
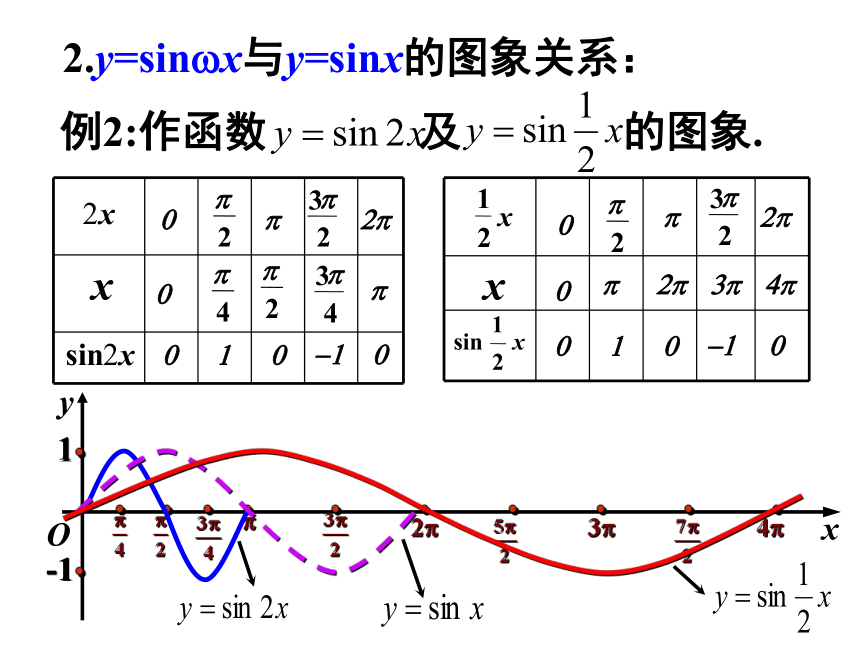
2.y=sin?x与y=sinx的图象关系:
例2:作函数 及 的图象.
p
2p
2
p
2
3
p
0
4
p
2
p
4
3
p
p
0
x
2
1
sin
x
x
1
0
0
-1
0
p
2p
2
p
2
3
p
0
x
2
1
1
0
0
-1
0
p
2p
3p
4p
0
y
O
x
-1
1
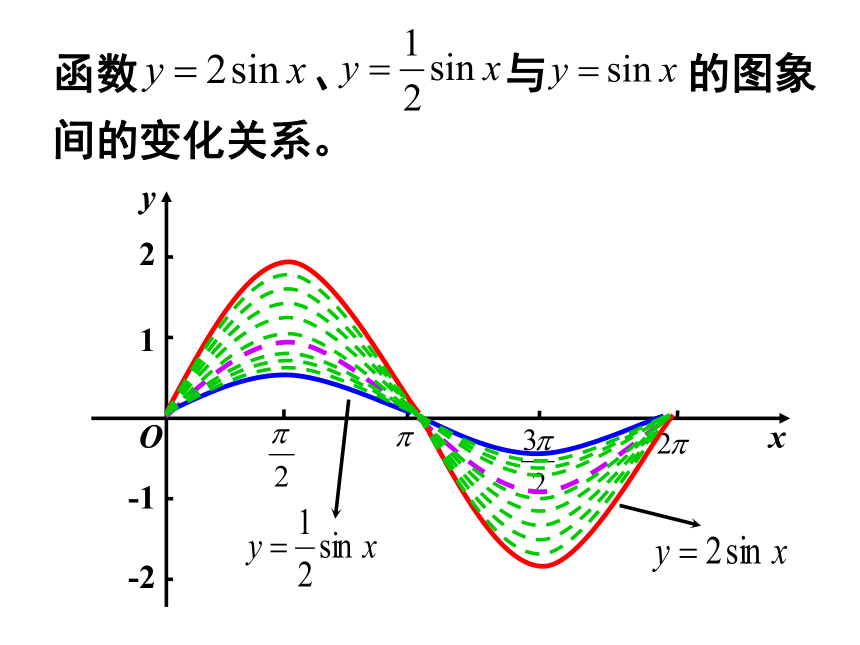
函数 、 与 的图象间的变化关系。
-1
y
O
x
1
所有的点横坐标缩短(?>1)或伸长(0< ?<1) 1/?倍
二、函数y=sin?x(?>0)图象:
函数 y=sin?x (?>0且??0) 的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当0< ?<1时)到原来的1/?倍(纵坐标不变)而得到的。
周期变换
y=sinx
y=sin?x
纵坐标不变
?决定函数的周期:
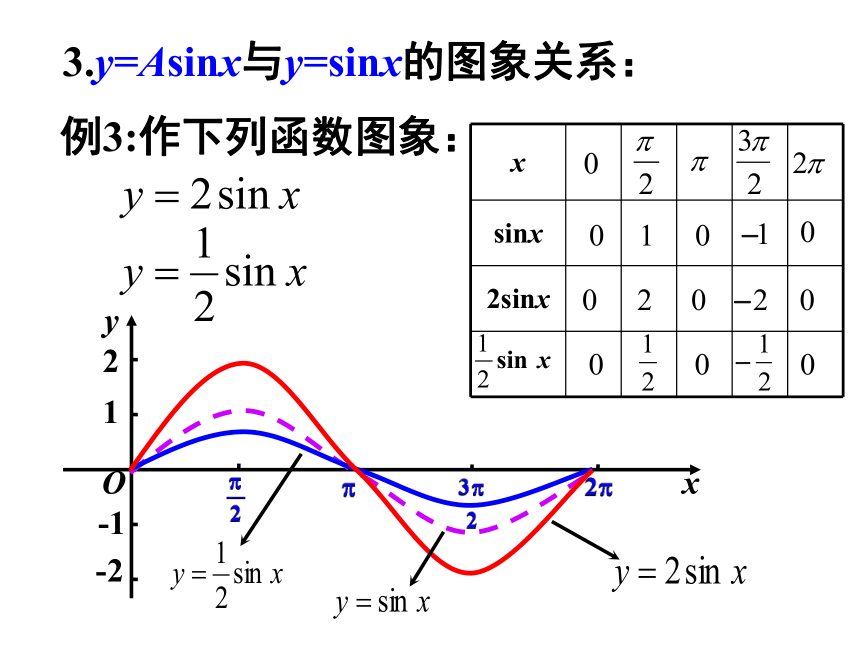
3.y=Asinx与y=sinx的图象关系:
2sinx
sinx
x
例3:作下列函数图象:
x
O
1
-1
y
2
-2
函数 、 与 的图象间的变化关系。
x
O
1
-1
y
2
-2
振幅变换
y=sinx
y=Asinx
所有的点纵坐标伸长(A>1)或缩短(0< A<1) A倍
横坐标不变
三、函数y=Asinx(A>0)图象:
函数 y=Asinx(A>0且A?1) 的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0< A<1时)到原来的A倍(横坐标不变)而得到的。
A的大小决定这个函数的最大(小)值
y=Asinx,x?R的值域是[-A, A],
最大值是A,最小值是-A。
例4:如何由 变换得
的图象?
1
-1
2
-2
o
x
3
-3
y
方法1:(按 顺序变换)
1
-1
2
-2
o
x
3
-3
y
方法2:(按 顺序变换)
y=sinx
y=sin(x+?)
横坐标缩短?>1 (伸长0y=sin(?x+?)
纵坐标伸长A>1 (缩短0y=Asin(?x+?)
y=sinx
y=Asin(?x+?)
总结:
向左?>0 (向右?<0)
方法1:(按 顺序变换)
平移|?|个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短?>1 (伸长0y=sin?x
纵坐标伸长A>1 (缩短0y=Asin(?x+?)
y=sinx
y=Asin(?x+?)
总结:
纵坐标不变
横坐标不变
方法2:(按 顺序变换)
向左?>0 (向右?<0)
平移|?|/?个单位
x/s
y/cm
O
A
B
C
D
E
F
2-
0.4
0.8
1.2
例5:图是某简谐运动的图象。
(1)这个简谐运动
的振幅、周期与
频率各是多少?
(2)从O点算起,到曲线上的哪一点,表示完成了一次往复运动?如从A点算起呢?
(3)求这个简谐运动的函数表达式.
例6:已知函数y=Asin(?x+?)(?>0, A>0)
的图像如下:
求解析式?
y
2
-2
O
x
总结:
利用 ,求得
选择的点要认清其属“五点法”中的哪一位置点,并能正确代人列式,求得 。
“第一点”为:
“第二点”为:
“第三点”为:
“第四点”为:
“第五点”为:
练习1:如图,某地一天从6~14时的温度变化曲线近似满足函数:
这段曲线对应的函数是什么?
T/度
t/h
O
6
10
14
10
20
30
练习2:海水受日月的引力,在一定的时候发生涨落的现象叫潮。一般地,早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋。下面是某港口在某季节每天的时间与水深关系表:
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
求函数解析式?
x
y
o
18
24
6
12
2
4
6
8
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
【总一总★成竹在胸】
所有的点向左(? >0)
或向右(? <0)平行移动
| ? | 个单位长度
y=sinx
y=sin(x+?)
y=sinx
y=sin?x
横坐标缩短(?>1)或
伸长(0< ?<1) 1/?倍
纵坐标不变
y=sinx
y=Asinx
纵坐标伸长(A>1)或
缩短(0< A<1) A倍
横坐标不变
(2)y=sinx与y=sin?x的图象关系;
(3)y=sinx与y=Asinx的图象关系;
(4)y=sinx与y=Asin(?x+?)的图象关系。
y
x
O
1
1
***复习回顾***
1.y=sin(x+?)与y=sinx的图象关系:
例1:试研究 与 的图象关系.
y
1
-1
O
x
所有的点向左(? >0)
或向右(? <0)平移
| ? | 个单位
一、函数y=sin(x+?)图象:
函数 y=sin(x+?)(??0) 的图象可以看作是把y=sinx 的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动|?|个单位而得到的.
y=sinx
y=sin(x+?)
?的变化引起图象位置发生变化(左加右减)
平移变换
2.y=sin?x与y=sinx的图象关系:
例2:作函数 及 的图象.
p
2p
2
p
2
3
p
0
4
p
2
p
4
3
p
p
0
x
2
1
sin
x
x
1
0
0
-1
0
p
2p
2
p
2
3
p
0
x
2
1
1
0
0
-1
0
p
2p
3p
4p
0
y
O
x
-1
1
函数 、 与 的图象间的变化关系。
-1
y
O
x
1
所有的点横坐标缩短(?>1)或伸长(0< ?<1) 1/?倍
二、函数y=sin?x(?>0)图象:
函数 y=sin?x (?>0且??0) 的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当0< ?<1时)到原来的1/?倍(纵坐标不变)而得到的。
周期变换
y=sinx
y=sin?x
纵坐标不变
?决定函数的周期:
3.y=Asinx与y=sinx的图象关系:
2sinx
sinx
x
例3:作下列函数图象:
x
O
1
-1
y
2
-2
函数 、 与 的图象间的变化关系。
x
O
1
-1
y
2
-2
振幅变换
y=sinx
y=Asinx
所有的点纵坐标伸长(A>1)或缩短(0< A<1) A倍
横坐标不变
三、函数y=Asinx(A>0)图象:
函数 y=Asinx(A>0且A?1) 的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0< A<1时)到原来的A倍(横坐标不变)而得到的。
A的大小决定这个函数的最大(小)值
y=Asinx,x?R的值域是[-A, A],
最大值是A,最小值是-A。
例4:如何由 变换得
的图象?
1
-1
2
-2
o
x
3
-3
y
方法1:(按 顺序变换)
1
-1
2
-2
o
x
3
-3
y
方法2:(按 顺序变换)
y=sinx
y=sin(x+?)
横坐标缩短?>1 (伸长0y=sin(?x+?)
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin(?x+?)
总结:
向左?>0 (向右?<0)
方法1:(按 顺序变换)
平移|?|个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短?>1 (伸长0y=sin?x
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin(?x+?)
总结:
纵坐标不变
横坐标不变
方法2:(按 顺序变换)
向左?>0 (向右?<0)
平移|?|/?个单位
x/s
y/cm
O
A
B
C
D
E
F
2-
0.4
0.8
1.2
例5:图是某简谐运动的图象。
(1)这个简谐运动
的振幅、周期与
频率各是多少?
(2)从O点算起,到曲线上的哪一点,表示完成了一次往复运动?如从A点算起呢?
(3)求这个简谐运动的函数表达式.
例6:已知函数y=Asin(?x+?)(?>0, A>0)
的图像如下:
求解析式?
y
2
-2
O
x
总结:
利用 ,求得
选择的点要认清其属“五点法”中的哪一位置点,并能正确代人列式,求得 。
“第一点”为:
“第二点”为:
“第三点”为:
“第四点”为:
“第五点”为:
练习1:如图,某地一天从6~14时的温度变化曲线近似满足函数:
这段曲线对应的函数是什么?
T/度
t/h
O
6
10
14
10
20
30
练习2:海水受日月的引力,在一定的时候发生涨落的现象叫潮。一般地,早潮叫潮,晚潮叫汐。在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋。下面是某港口在某季节每天的时间与水深关系表:
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
求函数解析式?
x
y
o
18
24
6
12
2
4
6
8
5.0
2.5
5.0
7.5
5.0
2.5
5.0
7.5
5.0
水深/米
24
21
18
15
12
9
6
3
0
时刻
【总一总★成竹在胸】
所有的点向左(? >0)
或向右(? <0)平行移动
| ? | 个单位长度
y=sinx
y=sin(x+?)
y=sinx
y=sin?x
横坐标缩短(?>1)或
伸长(0< ?<1) 1/?倍
纵坐标不变
y=sinx
y=Asinx
纵坐标伸长(A>1)或
缩短(0< A<1) A倍
横坐标不变
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
