2 3二次函数与一元二次方程、不等式 (备课件)--2021-2022学年高一数学同步备课系列(人教A版2019必修第一册)(23张PPT)
文档属性
| 名称 | 2 3二次函数与一元二次方程、不等式 (备课件)--2021-2022学年高一数学同步备课系列(人教A版2019必修第一册)(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-12 20:44:32 | ||
图片预览







文档简介
第2章 一元二次函数、方程和不等式
2.3 二次函数与一元二次方程、不等式
人教A版2019高中数学必修第一册
函数、方程、不等式知识回顾
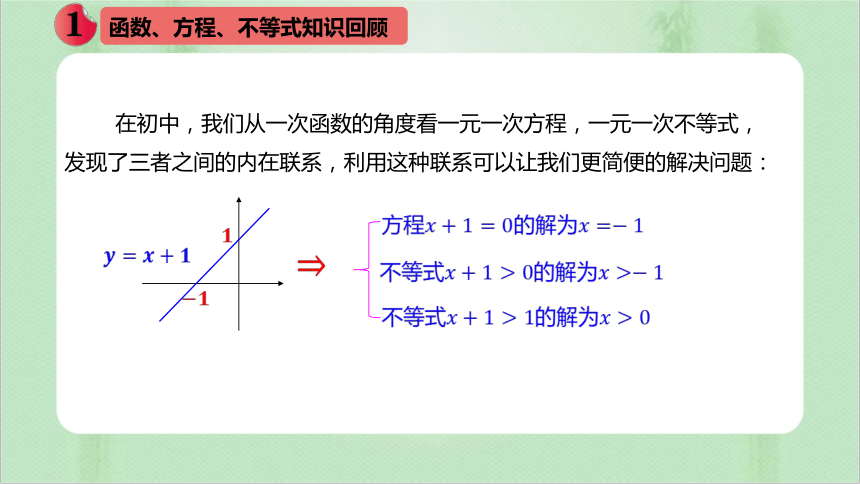
在初中,我们从一次函数的角度看一元一次方程,一元一次不等式,
发现了三者之间的内在联系,利用这种联系可以让我们更简便的解决问题:
????=????+????
?
?
?
方程????+1=0的解为????=?1
?
?????
?
????
?
不等式????+1>0的解为????>?1
?
不等式????+1>1的解为????>0
?
函数、方程、不等式知识回顾
对于二次函数、一元二次方程和一元二次不等式,
他们的联系又是怎样的呢?
????=????????????+????????+????
?
????????????+????????+????=????
?
????????????+????????+????>????
?
一元二次不等式的概念
【问题】园艺师傅打算在绿地上用栅栏围成一个矩形区域种
植花卉,若栅栏的长度是24 m,围成的矩形区域的面积要大
于20 m 2,则这个矩形的长和宽应该是多少?
【解】由题意设这个矩形的两条边长分别为????米和12?????米,则:
?
????12?????>20,其中????∈????0?
整理得????2?12????+20<0,????∈????0?
解得2?
即?????2?????10<0,?????2>0,?????10<0或?????2<0,?????10>0
?
一元二次不等式的概念
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,
称为一元二次不等式.它的一般形式是
????????????+????????+????>???? , ????????????+????????+????????????????+????????+????≥????,????????????+????????+????≤????,
其中????,????,????都是常数且???? ≠0.
?
二次函数的零点
在初中,我们学习了从一次函数的观点看一元一次次方程、一元一次不等式的思想方法.类似的,能否从二次函数的观点来看一元二次不等式,进而得到一元二次不等式的求解方法呢?
二次函数的零点
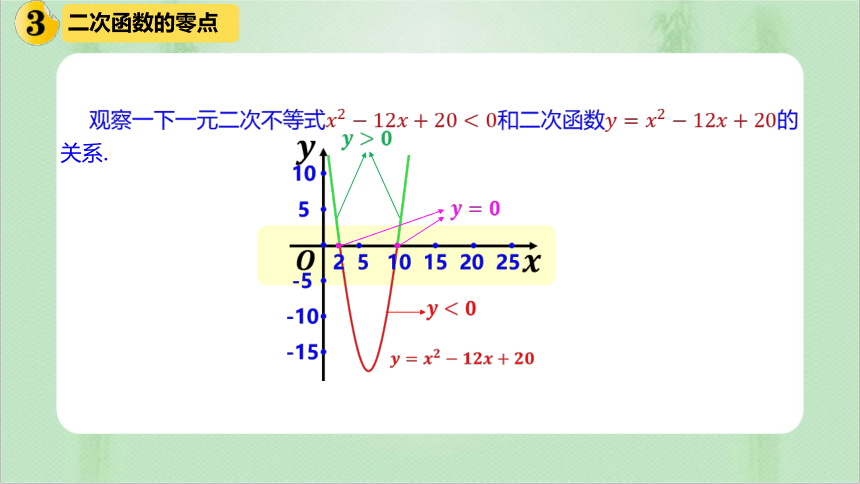
观察一下一元二次不等式????2?12????+20<0和二次函数????=????2?12????+20的
?
????>????
?
?????
????=????
?
关系.
一元二次不等式的解法
????????
?
????????
?
????????(????????)
?
两个不等实根????????,????????
????????+????????=?????????????(?????????
两个相等实根
????????=????????=?????????????
?
没有实数根
{????|????????????}
?
{????|????≠?????????????}
?
R
{????|?????????
?
?
【例题】求不等式????2?5????+6>0的解集.
?
【解】对于方程????2?5????+6=0,因为Δ>0,所以它有
两个实数根.解方程得????1=2,????2=3.画出函数
????=????2?5????+6的图像如图所示,
?
结合图像可知不等式????2?5????+6>0的解集为{????|????<2或????>3}
?
????
?
????
?
????
?
??????????????
?
????
?
一元二次不等式的应用
例题 一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的
的摩托车数量????(单位:辆)与创造的价值????(单位:元)之间有如下的关系:
????=?20????2+2200????,若这家工厂希望在一个星期
内利用这条流水线创收60000元以上,则应该生产
摩托车多少辆?
?
【解】设一星期内生产摩托车????辆,由题意有:
?
?????????????????+????????????????????>????????????????????,整理得????2?110????+3000<0,
?
方程????2?110????+3000=0有两个实数根????1=50,????2=60.
?
结合图像可知????2?110????+3000<0的解集为
{????|50?
????
?
????
?
????
?
???????????????????????
?
一元二次不等式的应用
跟踪练习 某种汽车在水泥路面上的刹车距离????(单位:米)和汽车刹车前的速度????(单位: km/h)之间有如下关系:????=1180????2+120????.再一次交通
事故中,测得这种车的刹车距离大于39.5米,那么
这辆车刹车前的速度至少为多少?
?
【解】根据题意得: 1180????2+120???? >39.5,整理得:
?
????????+?????????????????????????>????,方程????????+?????????????????????????=????有两个实数
根????1=?9?285212=?88, ????2=?9+285212=80,
?
结合图像可知????????+?????????????????????????>????的解集为
{????|????80},即车速至少为80 km/h.
?
????
?
????
?
????
?
????????????????????????????????
?
练习①:解关于????的不等式2????2+????????+2>0.
?
【解】对于方程2????2+????????+2=0,Δ=????2?16=????+4?????4
?
【解含参数的一元二次不等式】
因为Δ的正负未知,故需要分类讨论:
?
①当????>4或????????1=14??????????2?16,????2=14?????+????2?16
?
所以原不等式的解集为{????|}????<14??????????2?16或????>14?????+????2?16
?
②当????=4时, Δ=0,方程2????2+????????+2=0有两个相等实根????1=????2=?1
?
所以原不等式的解集为{????|}????≠?1
?
练习①:解关于????的不等式2????2+????????+2>0.
?
【解】对于方程2????2+????????+2=0,Δ=????2?16=????+4?????4
?
【解含参数的一元二次不等式】
因为Δ的正负未知,故需要分类讨论:
?
③当????=?4时, Δ=0,2????2+????????+2=0有两个相等实根????1=????2=1,
?
④当?4?
所以原不等式的解集为R
所以原不等式的解集为{????|????≠1}
?
练习②:已知不等式????????2?????????+2<0的解集为{????|1?
【方法1】由题设条件知????>0,且1,2是方程????????2?????????+2=0的两实根.
?
【三个“二次”的关系】
由韦达定理知1+2=????????,1×2=2????,
?
解得????=1,????=3,
?
【方法2】把????= 1 ????=2,分别代入方程????????2?????????+2=0中,
?
得?????????+2=0,4?????2????+2=0,
?
解得????=1,????=3,
?
练习③:不论????取何值,不等式????????2?2????+?????2<0恒成立,求????的取值范围.
?
【解】因为不等式????????2?2????+?????2<0恒成立,即函数????=????????2?2????+?????2
的图像全部在????轴下方.
?
【不等式恒成立的问题】
当????=0时,?2?????2<0,显然对任意????不能恒成立;
?
当????≠0时,由二次函数图像可知有????<0,△=4?4????(?????2)<0
?
解得????<1?2
?
综上可知,解得????的取值范围是{????|????<1?2}
?
THANKS
“
”
2.3 二次函数与一元二次方程、不等式
人教A版2019高中数学必修第一册
函数、方程、不等式知识回顾
在初中,我们从一次函数的角度看一元一次方程,一元一次不等式,
发现了三者之间的内在联系,利用这种联系可以让我们更简便的解决问题:
????=????+????
?
?
?
方程????+1=0的解为????=?1
?
?????
?
????
?
不等式????+1>0的解为????>?1
?
不等式????+1>1的解为????>0
?
函数、方程、不等式知识回顾
对于二次函数、一元二次方程和一元二次不等式,
他们的联系又是怎样的呢?
????=????????????+????????+????
?
????????????+????????+????=????
?
????????????+????????+????>????
?
一元二次不等式的概念
【问题】园艺师傅打算在绿地上用栅栏围成一个矩形区域种
植花卉,若栅栏的长度是24 m,围成的矩形区域的面积要大
于20 m 2,则这个矩形的长和宽应该是多少?
【解】由题意设这个矩形的两条边长分别为????米和12?????米,则:
?
????12?????>20,其中????∈????0?
整理得????2?12????+20<0,????∈????0?
解得2?
即?????2?????10<0,?????2>0,?????10<0或?????2<0,?????10>0
?
一元二次不等式的概念
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,
称为一元二次不等式.它的一般形式是
????????????+????????+????>???? , ????????????+????????+????????????????+????????+????≥????,????????????+????????+????≤????,
其中????,????,????都是常数且???? ≠0.
?
二次函数的零点
在初中,我们学习了从一次函数的观点看一元一次次方程、一元一次不等式的思想方法.类似的,能否从二次函数的观点来看一元二次不等式,进而得到一元二次不等式的求解方法呢?
二次函数的零点
观察一下一元二次不等式????2?12????+20<0和二次函数????=????2?12????+20的
?
????>????
?
?????
????=????
?
关系.
一元二次不等式的解法
????????
?
????????
?
????????(????????)
?
两个不等实根????????,????????
????????+????????=?????????????(?????????
两个相等实根
????????=????????=?????????????
?
没有实数根
{????|????????????}
?
{????|????≠?????????????}
?
R
{????|?????????
?
?
【例题】求不等式????2?5????+6>0的解集.
?
【解】对于方程????2?5????+6=0,因为Δ>0,所以它有
两个实数根.解方程得????1=2,????2=3.画出函数
????=????2?5????+6的图像如图所示,
?
结合图像可知不等式????2?5????+6>0的解集为{????|????<2或????>3}
?
????
?
????
?
????
?
??????????????
?
????
?
一元二次不等式的应用
例题 一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的
的摩托车数量????(单位:辆)与创造的价值????(单位:元)之间有如下的关系:
????=?20????2+2200????,若这家工厂希望在一个星期
内利用这条流水线创收60000元以上,则应该生产
摩托车多少辆?
?
【解】设一星期内生产摩托车????辆,由题意有:
?
?????????????????+????????????????????>????????????????????,整理得????2?110????+3000<0,
?
方程????2?110????+3000=0有两个实数根????1=50,????2=60.
?
结合图像可知????2?110????+3000<0的解集为
{????|50?
????
?
????
?
????
?
???????????????????????
?
一元二次不等式的应用
跟踪练习 某种汽车在水泥路面上的刹车距离????(单位:米)和汽车刹车前的速度????(单位: km/h)之间有如下关系:????=1180????2+120????.再一次交通
事故中,测得这种车的刹车距离大于39.5米,那么
这辆车刹车前的速度至少为多少?
?
【解】根据题意得: 1180????2+120???? >39.5,整理得:
?
????????+?????????????????????????>????,方程????????+?????????????????????????=????有两个实数
根????1=?9?285212=?88, ????2=?9+285212=80,
?
结合图像可知????????+?????????????????????????>????的解集为
{????|????80},即车速至少为80 km/h.
?
????
?
????
?
????
?
????????????????????????????????
?
练习①:解关于????的不等式2????2+????????+2>0.
?
【解】对于方程2????2+????????+2=0,Δ=????2?16=????+4?????4
?
【解含参数的一元二次不等式】
因为Δ的正负未知,故需要分类讨论:
?
①当????>4或????????1=14??????????2?16,????2=14?????+????2?16
?
所以原不等式的解集为{????|}????<14??????????2?16或????>14?????+????2?16
?
②当????=4时, Δ=0,方程2????2+????????+2=0有两个相等实根????1=????2=?1
?
所以原不等式的解集为{????|}????≠?1
?
练习①:解关于????的不等式2????2+????????+2>0.
?
【解】对于方程2????2+????????+2=0,Δ=????2?16=????+4?????4
?
【解含参数的一元二次不等式】
因为Δ的正负未知,故需要分类讨论:
?
③当????=?4时, Δ=0,2????2+????????+2=0有两个相等实根????1=????2=1,
?
④当?4?
所以原不等式的解集为R
所以原不等式的解集为{????|????≠1}
?
练习②:已知不等式????????2?????????+2<0的解集为{????|1?
【方法1】由题设条件知????>0,且1,2是方程????????2?????????+2=0的两实根.
?
【三个“二次”的关系】
由韦达定理知1+2=????????,1×2=2????,
?
解得????=1,????=3,
?
【方法2】把????= 1 ????=2,分别代入方程????????2?????????+2=0中,
?
得?????????+2=0,4?????2????+2=0,
?
解得????=1,????=3,
?
练习③:不论????取何值,不等式????????2?2????+?????2<0恒成立,求????的取值范围.
?
【解】因为不等式????????2?2????+?????2<0恒成立,即函数????=????????2?2????+?????2
的图像全部在????轴下方.
?
【不等式恒成立的问题】
当????=0时,?2?????2<0,显然对任意????不能恒成立;
?
当????≠0时,由二次函数图像可知有????<0,△=4?4????(?????2)<0
?
解得????<1?2
?
综上可知,解得????的取值范围是{????|????<1?2}
?
THANKS
“
”
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
