苏科版 八年级数学上册 3.1 勾股定理 一课一练 习题(Word版 含答案)
文档属性
| 名称 | 苏科版 八年级数学上册 3.1 勾股定理 一课一练 习题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 403.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 00:00:00 | ||
图片预览


文档简介
3.1《勾股定理》习题
一、选择题
1.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是(??
)
A.51
B.49
C.76
D.无法确定
2.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是( )
A.S1=2
B.S2=3
C.S3=6
D.S1+S3=8
3.如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走(
)
A.800m
B.1000m
C.1200m
D.1500m
4.如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm
B.30cm
C.2cm
D.4cm
5.圆柱形杯子的高为18cm,底面周长为24cm,已知蚂蚁在外壁A处(距杯子上沿2cm)发现一滴蜂蜜在杯子内(距杯子下沿4cm),则蚂蚁从A处爬到B处的最短距离为(
)
A.
B.28
C.20
D.
6.如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )
A.10尺
B.11尺
C.12尺
D.13尺
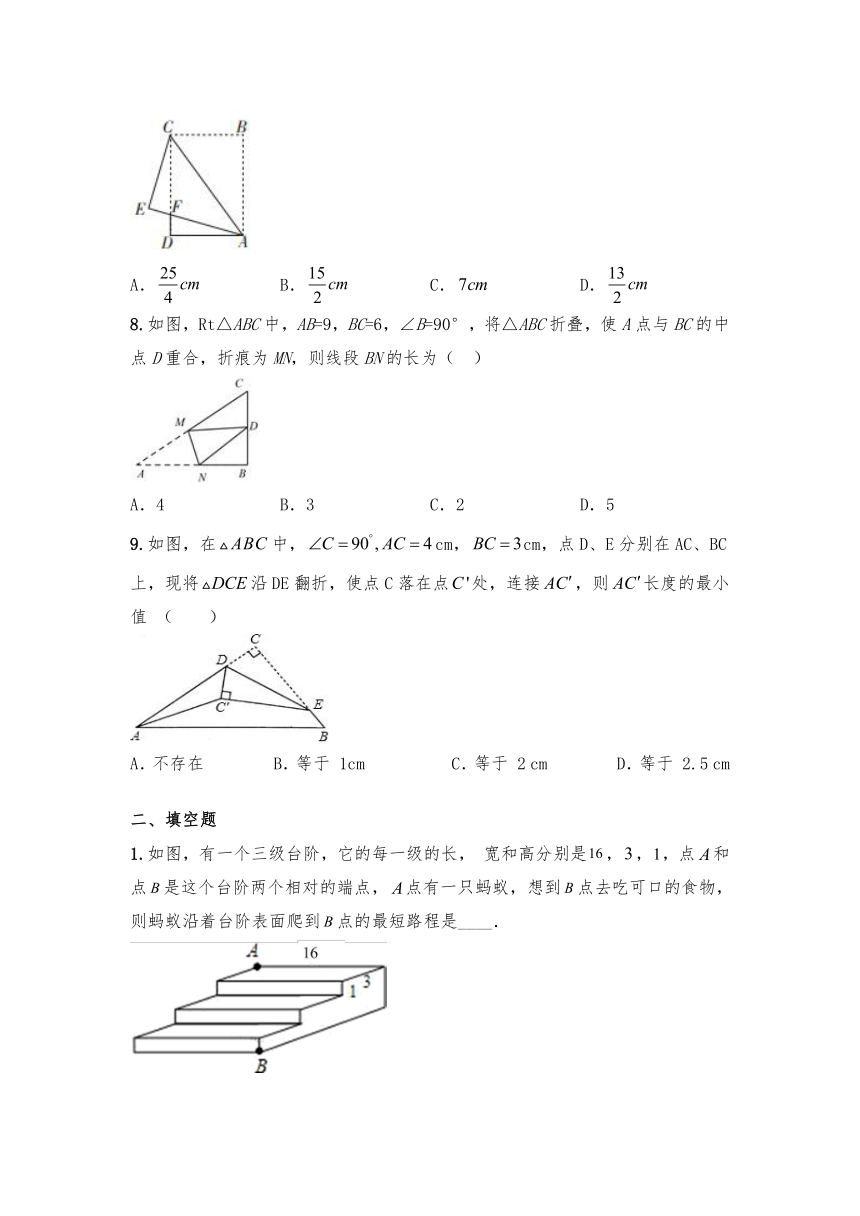
7.如图,在长方形纸片中,,.
把长方形纸片沿直线折叠,点落在点处,交于点,则的长为(
)
A.
B.
C.
D.
8.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为(
)
A.4
B.3
C.2
D.5
9.如图,在中,cm,cm,点D、E分别在AC、BC上,现将沿DE翻折,使点C落在点处,连接,则长度的最小值
(
)
A.不存在
B.等于
1cm
C.等于
2
cm
D.等于
2.5
cm
二、填空题
1.如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶表面爬到点的最短路程是____.
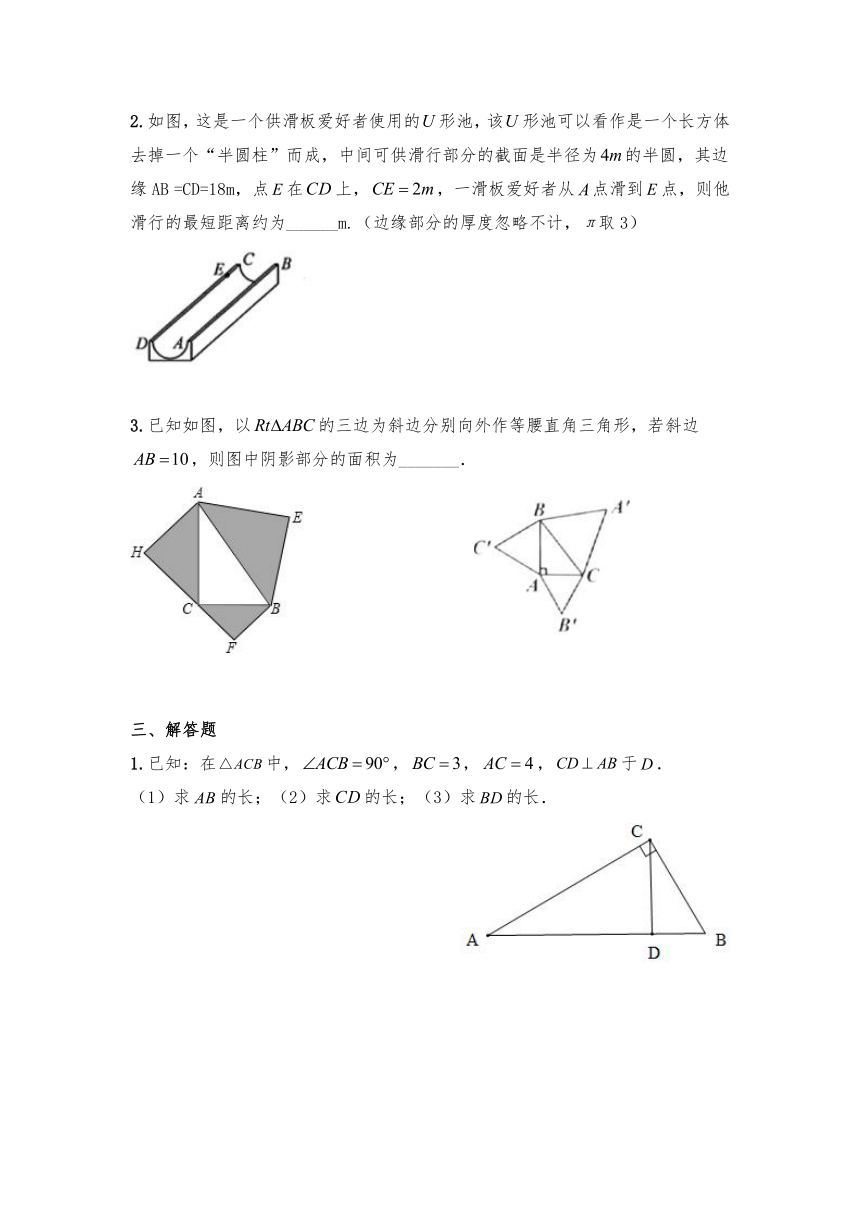
2.如图,这是一个供滑板爱好者使用的形池,该形池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为的半圆,其边缘AB
=CD=18m,点在上,,一滑板爱好者从点滑到点,则他滑行的最短距离约为______m.(边缘部分的厚度忽略不计,π取3)
3.已知如图,以的三边为斜边分别向外作等腰直角三角形,若斜边,则图中阴影部分的面积为_______.
三、解答题
1.已知:在中,,,,于.
(1)求的长;(2)求的长;(3)求的长.
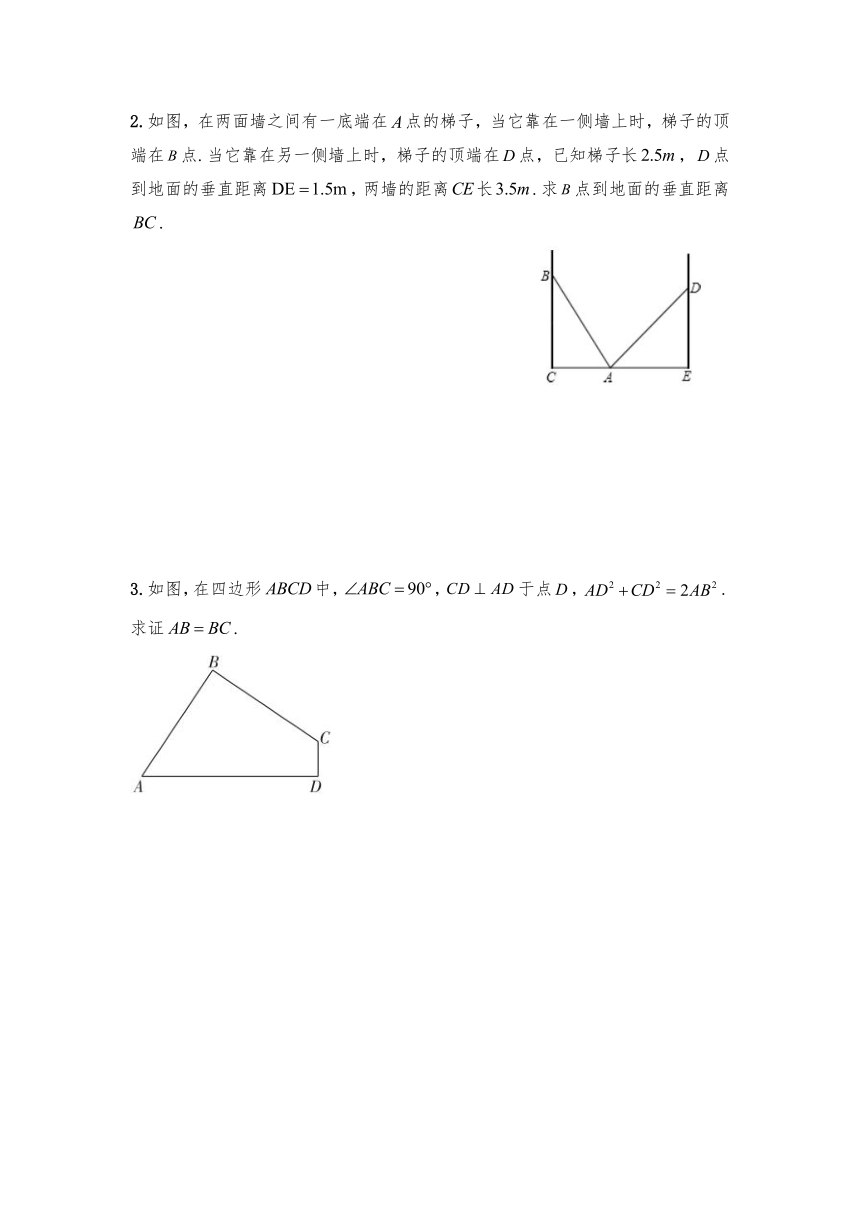
2.如图,在两面墙之间有一底端在点的梯子,当它靠在一侧墙上时,梯子的顶端在点.当它靠在另一侧墙上时,梯子的顶端在点,已知梯子长,点到地面的垂直距离,两墙的距离长.求点到地面的垂直距离.
3.如图,在四边形中,,于点,.求证.
4.有一架秋千,当它静止时,踏板离地的垂直高度DE=1m,将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m,秋千的绳索始终拉得很直,求绳索AD的长度.
5.如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
6.如图,有一张直角三角形纸片,两直角边,,将折叠,使点B与点C重合,折痕为.(1)求的周长;(2)求DE的长.
7.如图,折叠长方形的一边,使点落在边上的点处,,.(1)求的长;(2)求的长.
答案
一、选择题
1.C.
2.D.
3.B.
4.B.
5.C.
6.D.
7.A.
8.A.
9.C.
二、填空题
1.20
2.20m
3.50
三、解答题
1.解:(1)∵中,,,
∴根据勾股定理,,即,解得;
(2)∵,∴,即,解得;
(3)在Rt△BCD中,根据勾股定理,即,解得.
2.由题意得:,,,
在中,
即
在中,即
答:点到地面的垂直距离为.
3.证明:连接.
∵,∴.∵,∴.
∵,∴.∴.∴.
4.解:在Rt△ACB中,AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣3)m,故x2=62+(x﹣3)2,解得:x=7.5,
答:绳索AD的长度是7.5m.
5.解:设AE=xkm,∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25﹣x)2,x=10.故:E点应建在距A站10千米处.
6.解:(1)由题意得:
(2)由对折可得:,设
则
由
由对折可得:
7.解:(1)由题意可得,
在中,∵,
∴
(2)∵
由题意可得,设的长为cm
则在中,
解得
则的长为
一、选择题
1.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是(??
)
A.51
B.49
C.76
D.无法确定
2.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是( )
A.S1=2
B.S2=3
C.S3=6
D.S1+S3=8
3.如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走(
)
A.800m
B.1000m
C.1200m
D.1500m
4.如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm
B.30cm
C.2cm
D.4cm
5.圆柱形杯子的高为18cm,底面周长为24cm,已知蚂蚁在外壁A处(距杯子上沿2cm)发现一滴蜂蜜在杯子内(距杯子下沿4cm),则蚂蚁从A处爬到B处的最短距离为(
)
A.
B.28
C.20
D.
6.如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )
A.10尺
B.11尺
C.12尺
D.13尺
7.如图,在长方形纸片中,,.
把长方形纸片沿直线折叠,点落在点处,交于点,则的长为(
)
A.
B.
C.
D.
8.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为(
)
A.4
B.3
C.2
D.5
9.如图,在中,cm,cm,点D、E分别在AC、BC上,现将沿DE翻折,使点C落在点处,连接,则长度的最小值
(
)
A.不存在
B.等于
1cm
C.等于
2
cm
D.等于
2.5
cm
二、填空题
1.如图,有一个三级台阶,它的每一级的长,
宽和高分别是,,,点和点是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶表面爬到点的最短路程是____.
2.如图,这是一个供滑板爱好者使用的形池,该形池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为的半圆,其边缘AB
=CD=18m,点在上,,一滑板爱好者从点滑到点,则他滑行的最短距离约为______m.(边缘部分的厚度忽略不计,π取3)
3.已知如图,以的三边为斜边分别向外作等腰直角三角形,若斜边,则图中阴影部分的面积为_______.
三、解答题
1.已知:在中,,,,于.
(1)求的长;(2)求的长;(3)求的长.
2.如图,在两面墙之间有一底端在点的梯子,当它靠在一侧墙上时,梯子的顶端在点.当它靠在另一侧墙上时,梯子的顶端在点,已知梯子长,点到地面的垂直距离,两墙的距离长.求点到地面的垂直距离.
3.如图,在四边形中,,于点,.求证.
4.有一架秋千,当它静止时,踏板离地的垂直高度DE=1m,将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m,秋千的绳索始终拉得很直,求绳索AD的长度.
5.如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
6.如图,有一张直角三角形纸片,两直角边,,将折叠,使点B与点C重合,折痕为.(1)求的周长;(2)求DE的长.
7.如图,折叠长方形的一边,使点落在边上的点处,,.(1)求的长;(2)求的长.
答案
一、选择题
1.C.
2.D.
3.B.
4.B.
5.C.
6.D.
7.A.
8.A.
9.C.
二、填空题
1.20
2.20m
3.50
三、解答题
1.解:(1)∵中,,,
∴根据勾股定理,,即,解得;
(2)∵,∴,即,解得;
(3)在Rt△BCD中,根据勾股定理,即,解得.
2.由题意得:,,,
在中,
即
在中,即
答:点到地面的垂直距离为.
3.证明:连接.
∵,∴.∵,∴.
∵,∴.∴.∴.
4.解:在Rt△ACB中,AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣3)m,故x2=62+(x﹣3)2,解得:x=7.5,
答:绳索AD的长度是7.5m.
5.解:设AE=xkm,∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25﹣x)2,x=10.故:E点应建在距A站10千米处.
6.解:(1)由题意得:
(2)由对折可得:,设
则
由
由对折可得:
7.解:(1)由题意可得,
在中,∵,
∴
(2)∵
由题意可得,设的长为cm
则在中,
解得
则的长为
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
