北师大版九年级数学下册试题 2.4 《二次函数的应用》一课一练(word版含答案)
文档属性
| 名称 | 北师大版九年级数学下册试题 2.4 《二次函数的应用》一课一练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 352.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 00:00:00 | ||
图片预览



文档简介
2.4
《二次函数的应用》习题2
一、选择题
1.超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板(
)平方厘米.(不计重合部分)
A.253
B.288
C.206
D.245
2.竖直上抛物体离地面的高度与运动时间之间的关系可以近似地用公式表示,其中是物体抛出时离地面的高度,是物体抛出时的速度.某人将一个小球从距地面的高处以的速度竖直向上抛出,小球达到的离地面的最大高度为(
)
A.
B.
C.
D.
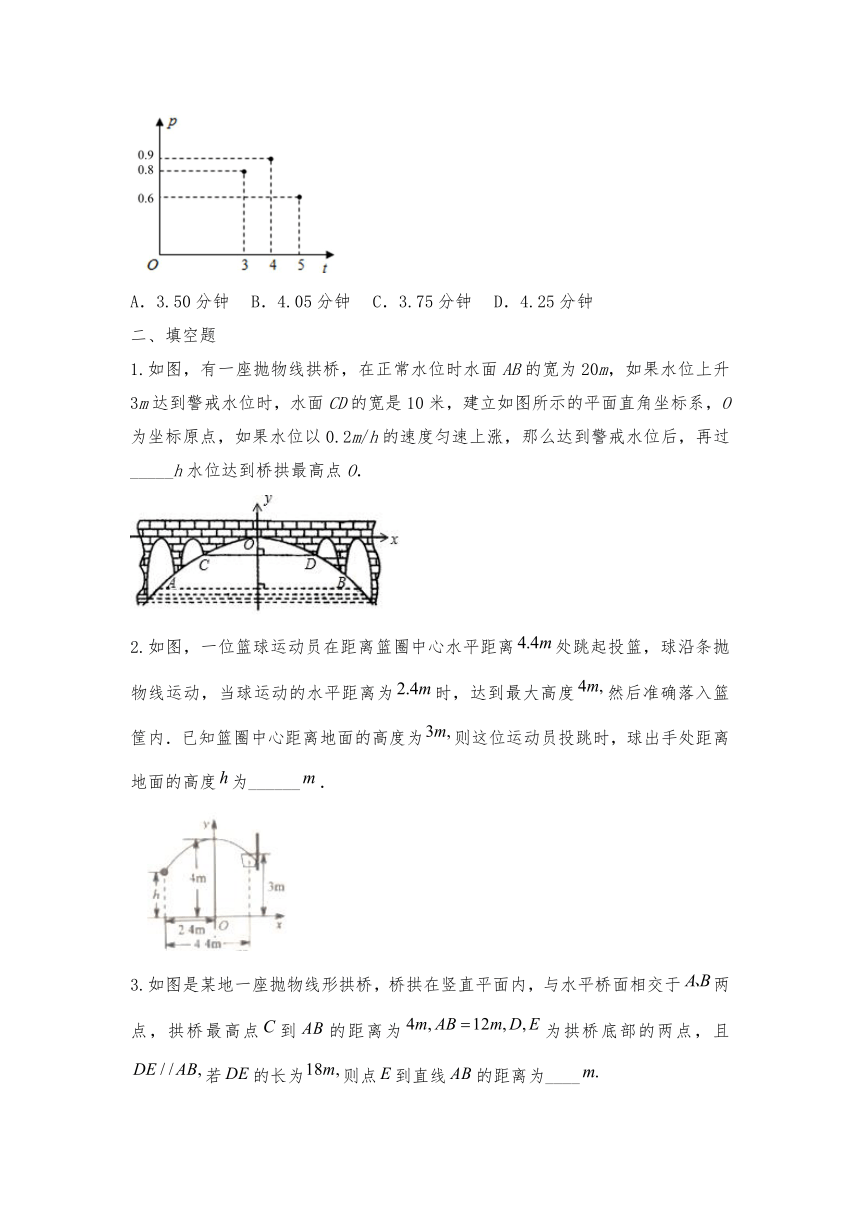
3.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式:(a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为(
)
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
二、填空题
1.如图,有一座抛物线拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10米,建立如图所示的平面直角坐标系,O为坐标原点,如果水位以0.2m/h的速度匀速上涨,那么达到警戒水位后,再过_____h水位达到桥拱最高点O.
2.如图,一位篮球运动员在距离篮圈中心水平距离处跳起投篮,球沿条抛物线运动,当球运动的水平距离为时,达到最大高度然后准确落入篮筐内.已知篮圈中心距离地面的高度为则这位运动员投跳时,球出手处距离地面的高度为______.
3.如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于两点,拱桥最高点到的距离为为拱桥底部的两点,且若的长为则点到直线的距离为____
4.如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面2米高时,水面为4米,则当水面下降1米时,水面宽度增加__________米.
三、解答题
1.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设的长度为米,矩形区域的面积为米.
求证:;
求与之间的函数关系式,并写出自变量的取值范围;
为何值时,有最大值?最大值是多少?
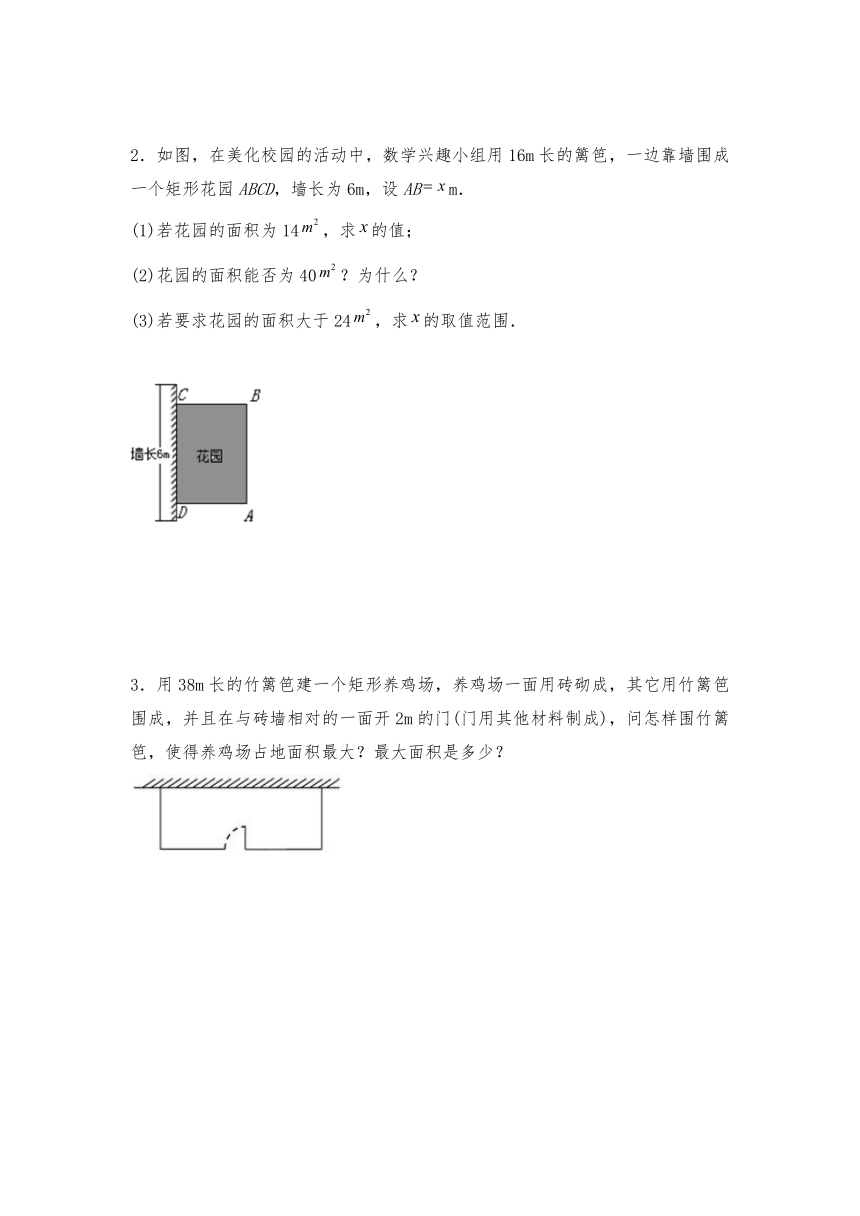
2.如图,在美化校园的活动中,数学兴趣小组用16m长的篱笆,一边靠墙围成一个矩形花园ABCD,墙长为6m,设ABm.
(1)若花园的面积为14,求的值;
(2)花园的面积能否为40?为什么?
(3)若要求花园的面积大于24,求的取值范围.
3.用38m长的竹篱笆建一个矩形养鸡场,养鸡场一面用砖砌成,其它用竹篱笆围成,并且在与砖墙相对的一面开2m的门(门用其他材料制成),问怎样围竹篱笆,使得养鸡场占地面积最大?最大面积是多少?
4.如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长24m.设AB长为x
m,矩形的面积为S
m2.
(1)写出S与x的函数关系式;
(2)当AB长为多少米时,所围成的花圃面积最大?最大值是多少?
(3)当花圃的面积为150m2时,AB长为多少米?
5.四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:
(1)为尽可能让利于顾客,赢得市场,每千克核桃应降价多少元?
(2)若该专卖店想获得最大利润W,核桃的单价应定为多少元?最大利润是多少?
6.“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行,某自行车店在销售某型号自行车时,标价1500元.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价是多少元?
(2)若该型号自行车的进价不变,按标价出售,该店平均每月可售出60辆:若每辆自行车每降价50元,每月可多售出10辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
7.一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件)
4
5
6
y(件)
10000
9500
9000
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
8.某水果店经销A、B两种水果,A种水果进货单价比B种水果进货单价多2元,花50元购进A种水果的数量与花40元购进B种水果的数量相同.在销售过程中发现,A种水果每天销售量是与销售价x(元)满足关系式,B种水果,每天销售量与销售价x(元)满足=
-x+14
(1)求A、B两种水果的单价.
(2)已知A种水果比B种水果的销售价高2元/千克,且每天A、B水果均有a千克坏掉.设B水果售价为t元/千克,每天两种水果的总利润为W元,求W与t的函数解析式,并求出当a的取值在什么范围内,水果店有可能不赔钱?
答案
一、选择题
1.A.
2.C
3.C
二、填空题
1.
5
2.2.56m.
3.
4.
三、解答题
1.解:∵三块矩形区域的面积相等,
∴矩形面积是矩形面积的倍,
又∵是公共边,
∴;
设,则,
∴,
∴,,
∴,
∵,
∴,
∴?
∵,且二次项系数为,
∴当时,有最大值,最大值为平方米.
2.(1)由题意列方程:,
解得14,2,
由于14>6不合题意,所以=2.
(2)设花园的面积为,依题意有:
,即,
的最大值=32,
∴花园的面积不能为40.
(3)由(2)知,
当=24时,有,解得12,4,
∵花园的面积大于24,∴4<<12,
又∵墙长为6m,∴0<≤6,
∴的取值范围是4<≤6.
3.
解:设垂直于墙的一边为m,则另一边为m,面积为.
,
∴当时,养鸡场的面积有最大值200m2,
即平行于墙的一边为20m,垂直于墙的一边为10m时,养鸡场占地面积最大,最大面积是200m2
4.解:(1)S=x(40﹣2x)=﹣2x2+40x,
即函数关系式为:S=﹣2x2+40x;
(2)由题意,得:0<40﹣2x≤24,
解得8≤x<20,
又由(1),得S=﹣2(x﹣10)2+200,
∴当x=10时,所围成的花圃面积最大,最大值为200m2;
(3)由﹣2(x﹣10)2+200=150,
解得
x1=5,x2=15,
∵8≤x<20,
∴当花圃的面积为150m2时,AB长为15米.
5.解:(1)设每千克核桃应降价x元,则每千克利润为(60﹣x﹣40)元,则每天销量为(100+)
(60﹣x﹣40)(100+)=2240,
解得,x1=4,x2=6,
∵要尽可能让利于顾客,
∵要尽可能让利于顾客,
∴每千克核桃应降价6元;
(2)设每千克核桃应降价y元,则每千克利润为(60﹣y﹣40)元,则每天销量为(100+)
则W=(60﹣y﹣40)(100+)=﹣10(y﹣5)2+2250,
∴当y=5时,W取得最大值,此时W=2250,
∴60﹣y=60﹣5=55,
∴该专卖店想获得最大利润W,核桃的单价应定为55元,最大利润是2250元.
6.解:(1)设进价为元
则:
解得:
∴改型号自行车进价1000元
(2)设自行车降价元,获利为元
则:
∴对称轴:,∵
∴当时,
答:降价100元时每月利润最大,最大为32000元.
7.解:(1)设y与x的函数关系式为y=kx+b,
代入(4,10000),(5,9500)可得:,
解得:,
即y与x的函数关系式为;
(2)设这一周该商场销售这种商品获得的利润为w,
根据题意可得:,
解得:,
∵,
∴当x=12时,w有最大值,w=54000,
答:这一周该商场销售这种商品获得的最大利润为54000元,售价为12元.
(3)设这一周该商场销售这种商品获得的利润为w,
当每销售一件商品便向某慈善机构捐赠m元时,
由题意,当x≤15时,利润仍随售价的增大而增大,
可得:,解得:m≥3,
∵
∴
故m的取值范围为:.
8.答案:(1)设水果B的进货单价为元/千克,则水果A的进货单价为()元/千克,
依题意得:,
解得:,
检验:经检验是原方程的解.
∴,
∴,
答:A种水果10元/千克,B种水果8元/千克;
(2)设B水果售价为元/千克,则A水果售价为()元/千克,
,
∵
-2<0
∴时,W(最大),
当时,
.
答:不超过时,水果可能不赔钱.
《二次函数的应用》习题2
一、选择题
1.超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板(
)平方厘米.(不计重合部分)
A.253
B.288
C.206
D.245
2.竖直上抛物体离地面的高度与运动时间之间的关系可以近似地用公式表示,其中是物体抛出时离地面的高度,是物体抛出时的速度.某人将一个小球从距地面的高处以的速度竖直向上抛出,小球达到的离地面的最大高度为(
)
A.
B.
C.
D.
3.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式:(a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为(
)
A.3.50分钟
B.4.05分钟
C.3.75分钟
D.4.25分钟
二、填空题
1.如图,有一座抛物线拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10米,建立如图所示的平面直角坐标系,O为坐标原点,如果水位以0.2m/h的速度匀速上涨,那么达到警戒水位后,再过_____h水位达到桥拱最高点O.
2.如图,一位篮球运动员在距离篮圈中心水平距离处跳起投篮,球沿条抛物线运动,当球运动的水平距离为时,达到最大高度然后准确落入篮筐内.已知篮圈中心距离地面的高度为则这位运动员投跳时,球出手处距离地面的高度为______.
3.如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于两点,拱桥最高点到的距离为为拱桥底部的两点,且若的长为则点到直线的距离为____
4.如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面2米高时,水面为4米,则当水面下降1米时,水面宽度增加__________米.
三、解答题
1.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设的长度为米,矩形区域的面积为米.
求证:;
求与之间的函数关系式,并写出自变量的取值范围;
为何值时,有最大值?最大值是多少?
2.如图,在美化校园的活动中,数学兴趣小组用16m长的篱笆,一边靠墙围成一个矩形花园ABCD,墙长为6m,设ABm.
(1)若花园的面积为14,求的值;
(2)花园的面积能否为40?为什么?
(3)若要求花园的面积大于24,求的取值范围.
3.用38m长的竹篱笆建一个矩形养鸡场,养鸡场一面用砖砌成,其它用竹篱笆围成,并且在与砖墙相对的一面开2m的门(门用其他材料制成),问怎样围竹篱笆,使得养鸡场占地面积最大?最大面积是多少?
4.如图,用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD,墙长24m.设AB长为x
m,矩形的面积为S
m2.
(1)写出S与x的函数关系式;
(2)当AB长为多少米时,所围成的花圃面积最大?最大值是多少?
(3)当花圃的面积为150m2时,AB长为多少米?
5.四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:
(1)为尽可能让利于顾客,赢得市场,每千克核桃应降价多少元?
(2)若该专卖店想获得最大利润W,核桃的单价应定为多少元?最大利润是多少?
6.“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行,某自行车店在销售某型号自行车时,标价1500元.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价是多少元?
(2)若该型号自行车的进价不变,按标价出售,该店平均每月可售出60辆:若每辆自行车每降价50元,每月可多售出10辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
7.一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件)
4
5
6
y(件)
10000
9500
9000
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠m元(),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.
8.某水果店经销A、B两种水果,A种水果进货单价比B种水果进货单价多2元,花50元购进A种水果的数量与花40元购进B种水果的数量相同.在销售过程中发现,A种水果每天销售量是与销售价x(元)满足关系式,B种水果,每天销售量与销售价x(元)满足=
-x+14
(1)求A、B两种水果的单价.
(2)已知A种水果比B种水果的销售价高2元/千克,且每天A、B水果均有a千克坏掉.设B水果售价为t元/千克,每天两种水果的总利润为W元,求W与t的函数解析式,并求出当a的取值在什么范围内,水果店有可能不赔钱?
答案
一、选择题
1.A.
2.C
3.C
二、填空题
1.
5
2.2.56m.
3.
4.
三、解答题
1.解:∵三块矩形区域的面积相等,
∴矩形面积是矩形面积的倍,
又∵是公共边,
∴;
设,则,
∴,
∴,,
∴,
∵,
∴,
∴?
∵,且二次项系数为,
∴当时,有最大值,最大值为平方米.
2.(1)由题意列方程:,
解得14,2,
由于14>6不合题意,所以=2.
(2)设花园的面积为,依题意有:
,即,
的最大值=32,
∴花园的面积不能为40.
(3)由(2)知,
当=24时,有,解得12,4,
∵花园的面积大于24,∴4<<12,
又∵墙长为6m,∴0<≤6,
∴的取值范围是4<≤6.
3.
解:设垂直于墙的一边为m,则另一边为m,面积为.
,
∴当时,养鸡场的面积有最大值200m2,
即平行于墙的一边为20m,垂直于墙的一边为10m时,养鸡场占地面积最大,最大面积是200m2
4.解:(1)S=x(40﹣2x)=﹣2x2+40x,
即函数关系式为:S=﹣2x2+40x;
(2)由题意,得:0<40﹣2x≤24,
解得8≤x<20,
又由(1),得S=﹣2(x﹣10)2+200,
∴当x=10时,所围成的花圃面积最大,最大值为200m2;
(3)由﹣2(x﹣10)2+200=150,
解得
x1=5,x2=15,
∵8≤x<20,
∴当花圃的面积为150m2时,AB长为15米.
5.解:(1)设每千克核桃应降价x元,则每千克利润为(60﹣x﹣40)元,则每天销量为(100+)
(60﹣x﹣40)(100+)=2240,
解得,x1=4,x2=6,
∵要尽可能让利于顾客,
∵要尽可能让利于顾客,
∴每千克核桃应降价6元;
(2)设每千克核桃应降价y元,则每千克利润为(60﹣y﹣40)元,则每天销量为(100+)
则W=(60﹣y﹣40)(100+)=﹣10(y﹣5)2+2250,
∴当y=5时,W取得最大值,此时W=2250,
∴60﹣y=60﹣5=55,
∴该专卖店想获得最大利润W,核桃的单价应定为55元,最大利润是2250元.
6.解:(1)设进价为元
则:
解得:
∴改型号自行车进价1000元
(2)设自行车降价元,获利为元
则:
∴对称轴:,∵
∴当时,
答:降价100元时每月利润最大,最大为32000元.
7.解:(1)设y与x的函数关系式为y=kx+b,
代入(4,10000),(5,9500)可得:,
解得:,
即y与x的函数关系式为;
(2)设这一周该商场销售这种商品获得的利润为w,
根据题意可得:,
解得:,
∵,
∴当x=12时,w有最大值,w=54000,
答:这一周该商场销售这种商品获得的最大利润为54000元,售价为12元.
(3)设这一周该商场销售这种商品获得的利润为w,
当每销售一件商品便向某慈善机构捐赠m元时,
由题意,当x≤15时,利润仍随售价的增大而增大,
可得:,解得:m≥3,
∵
∴
故m的取值范围为:.
8.答案:(1)设水果B的进货单价为元/千克,则水果A的进货单价为()元/千克,
依题意得:,
解得:,
检验:经检验是原方程的解.
∴,
∴,
答:A种水果10元/千克,B种水果8元/千克;
(2)设B水果售价为元/千克,则A水果售价为()元/千克,
,
∵
-2<0
∴时,W(最大),
当时,
.
答:不超过时,水果可能不赔钱.
