北师大版九年级数学下册试题 1.5《解直角三角形及三角函数的应用》一课一练(word版含答案)
文档属性
| 名称 | 北师大版九年级数学下册试题 1.5《解直角三角形及三角函数的应用》一课一练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 514.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 17:01:36 | ||
图片预览




文档简介
《解直角三角形及三角函数的应用》习题
一、选择题
1.如图,下列判断正确的是(
).
A.看的仰角是
B.看的俯角是45°
C.C看B的俯角
D.在的南偏西
2.如图,在△ABC中,若∠C=90°,则(
)
A.sinA=
B.sinA=
C.cosA=
D.cosA=
3.如图所示,OP是∠AOC的平分线,点B在OP上,于点D,,点B到OA的距离为2,则AB长为(
)
A.2
B.
C.
D.3
4.在△ABC中,∠C=90°,sinB=,b=,则a等于(
)
A.
B.1
C.2
D.3
5.如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
A.270cm
B.210cm
C.180cm
D.96cm
6.在中,已知∠C=90°,∠A=40°,AC=3,则BC的长为( )
A.3sin40°
B.3sin50°
C.3tan40°
D.3tan50°
7.如图,点E从点A出发沿AB方向运动,点G从点B出发沿BC方向运动,同时出发且速度相同,DE=GFA.一直减小
B.一直不变
C.先减小后增大
D.先增大后减小
8.如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若千米,则点两点的距离为()千米.
A.4
B.
C.2
D.6
9.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CE平分∠ACB交AB于点E.EF⊥BC于点F,若EF=4,则线段AE的长为(
)
A.2
B.
C.2+2
D.3
10.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AEFG,则图中阴影部分的面积为(
)
A.
B.
C.1-
D.1-
11.如图,嘉琪在一座桥的附近试飞一架小型无人机,为了测量无人机飞行的高度,嘉琪通过操控装置测得无人机俯视桥头,的俯角分别为和,且,,在同一水平线上,已知桥米,则无人机的飞行高度(
)
A.15米
B.米
C.米
D.米
12.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200米
C.220米
D.100米
13.如图,学校某数学兴趣小组想测量操场对面旗杆的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,己知旗杆所在平台的高度为3.5米,则旗杆的高度为(
)(结果精确到0.1,参考数据:,).
A.19.8米
B.19.7米
C.18.3米
D.16.2米
14.如图所示,把多块大小不同的30°角三角板,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与x轴重合且点A的坐标为(2,0),∠ABO=30°,第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交x轴于点B1,第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交y轴于点B2,第四块三角板斜边B2B3与第三块三角板的斜边B1B2垂直且交x轴于点B3.按此规律继续下去,则线段OB2020的长为( )
A.2×()2020
B.2×()2021
C.()2020
D.()2021
二、填空题
15.如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为
米.
16.如图,为测量一座大厦AB的高度,当小明在C处时测得楼顶A的仰角为60°,接着沿BC方向行走30
m至D处时测得楼顶A的仰角为30°,
则大厦AB的高度是_______.
17.在△ABC中,(2sinA﹣1)2+=0,则△ABC的形状为________
18.知在中,AB=
AC=5,BC=6,则tanB的值为_____.
三、解答题
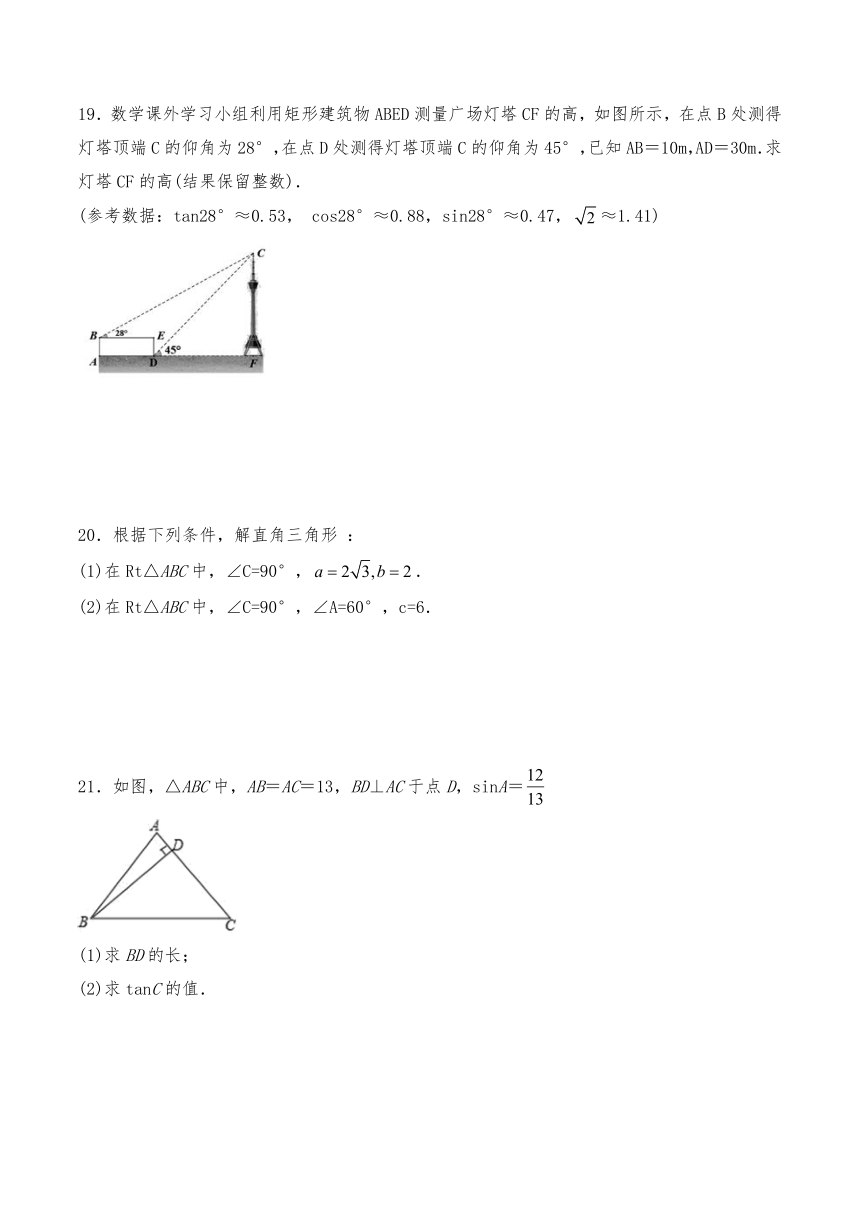
19.数学课外学习小组利用矩形建筑物ABED测量广场灯塔CF的高,如图所示,在点B处测得灯塔顶端C的仰角为28°,在点D处测得灯塔顶端C的仰角为45°,已知AB=10m,AD=30m.求灯塔CF的高(结果保留整数).
(参考数据:tan28°≈0.53,
cos28°≈0.88,sin28°≈0.47,≈1.41)
20.根据下列条件,解直角三角形
:
(1)在Rt△ABC中,∠C=90°,.
(2)在Rt△ABC中,∠C=90°,∠A=60°,c=6.
21.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
22.如图,四边形ABCD是矩形,以点A为圆心、AD为半径画弧交BC于
点E.DF⊥AE于F.若E恰好为BC的中点.
⑴
∠BAE=
°;
⑵
DF平分AE吗?证明你的结论.
23.如图,在边长为1个单位长度的小正方形组成的12×12的网格中,AB是以网络线的交点(格点)为端点的线段;
(1)将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段CD;
(2)以线段CD为一边,作一个菱形CDEF,连接DF,使,点E,F也为格点.
24.如图,052D型驱逐舰“昆明舰”执行任务后正返回葫芦岛军港C,途经渤海海域A处时,葫芦岛军港C的中国海军发现点A在南偏东30°方向上,旅顺军港B的中国海军发现点A在正西方向上.已知军港C在军港B的北偏西60°方向,且B、C两地相距120海里,(计算结果保留根号)
(1)求出此时点A到军港C的距离;
(2)若“昆明舰”从A处沿AC方向向军港C驶去,当到达A'时,测得军港B在A'的南偏东75°的方向上,求此时“昆明舰”的航行距离.
25.某“综合与实践”小组开展了测量本校对面山上一座古塔高度的实活动,他们制订了方案,并利用课余时间完成了实地测量.他们在该山脚的一块平地上,选择两个不同测点,分别测量山顶和塔顶的俯角,以及这两个测点之间的距离.为了减小测量误差,小组在测量俯角的度数以及两个测点之间的距离时,都分别测量了三次并取它们的平均值为测量结果,测量数据如下表(不完整).
课题
测量山上塔的高度
测量工具
测量角度的仪器,皮尺等
测量示意图
说明:线段表示山高,表示塔的高,测量角度的仪器的高度,端点B,C,D,A,E在同一竖直平面内,点D,C,B共线,点D,A,E共线.
测量数据
测量项目
第一次
第二次
第三次
平均值
的度数
63.6°
63.3°
63.3°
63.4°
的度数
29.9°
29.8°
30.3°
30°
的度数
44.9°
45.3°
44.8°
__________
A,E之间的距离
50.1m
49.8m
50.1m
__________
…
…
任务一:三次测量的度数平均值是__________;A,E之间的距离的平均值是__________m.
任务二,根据以上测量结果,请你帮助该“综合与实践”小组求出塔的高度.
(结果精确到0.1m.参考数据:,,,,)
26.阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即,,于是,即.
同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
答案
一、选择题
1.C.2.A.3.C.4.B.5.B.6.C.7.B.8.D.9.B.10.D.
11.B.12.D.13.C.14.B
二、填空题
15.
16.15
17.直角三角形.
18..
三、解答题
19.解:延长BE交CD于点G,交CF于点H,
在Rt中,∠EDG=45°,
∴EG=DE=10m.∠EGD=45°
设CH=xm,
在Rt中,∠EGD=45°,
∴GH=xm
在Rt中,∠CBH=28°,
∴tan∠CBH=,
即:=tan28°
解这个方程得:x≈45.1,
经检验:x≈45.1符合题意.
∴灯塔的高CF=55.1≈55(m)
答:灯塔的高为55米.
20.(1)∵在Rt△ABC中.∠C=90°,,
∴c===4,
∴c=2b,∠C=90°,
∴∠B=30°.
∴∠A=90°-30°=60°,
即:c=4,∠B=30°,∠A=60°;
(2)∵在Rt△ABC中.∠C=90°,∠A=60°,c=6,
∴∠B=∠C?∠A=90°?60°=30°.
∴c=2b.
∴b=3,
∴a===.
即a=,b=3,∠B=30°.
21.解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
22.解:(1)是以点A为圆心、AD为半径画弧得到的
四边形ABCD是矩形
点E恰好为BC的中点
(2)DF平分AE.
如图,连接DE
由(1)知,,
是等边三角形
所以DF平分AE.
23.(1)如图所示:线段CD即为所求;
(2)如图所示:菱形CDEF即为所求.
24.
解:(1)延长BA,过点C作CD⊥BA延长线于点D
由题意可得:∠CBD,BC=120
则DC=60
故
解得:AC=
答:此时点A到军港C的距离为海里;
(2)过点A'作A'N⊥BC于点N
可得∠1=,∠BA'A=
则∠2=,即A'B平分∠CBA
设AA'=x,则A'E=
故CA'=2A'N=
∵
∴
答:此时“昆明舰”的航行距离为海里.
25.解:任务一:∠BED的度数平均值==45?,A,E之间的距离的平均值==50,
任务一:45°;50.
任务二:∵在中,,
∴
∴①.
∵在中,,
∴,BD=2AD②,
由①与②得50+AD=2AD,AD=50,
∴ED=BD=100,
∵在中,,
∴
∴.
BC=BD-CD=100-.
∴.
答:塔的高度约为42.3m.
26.1)由题意得BC=60×0.5=30(海里),
∵CD∥BE,∠DCB=30°,
∴∠CBE=180°-∠DCB=150°,
∵∠ABE=75°,
∴∠ABC=150°-75°=75°,
∴∠A=180°-∠ABC-∠ACB=45°,
解得(海里)
所以货轮距灯塔A的距离AB为海里;
(2)过点B作BM⊥AC,在Rt△ABM中,∠A=45°,AB=,
∵,即,
∴AM=15,
在Rt△BMC中,∠BCM=60°,BC=30,则CM=BC(海里)
∴AC=AM+CM=()(海里)
∵
∴,
解得.
一、选择题
1.如图,下列判断正确的是(
).
A.看的仰角是
B.看的俯角是45°
C.C看B的俯角
D.在的南偏西
2.如图,在△ABC中,若∠C=90°,则(
)
A.sinA=
B.sinA=
C.cosA=
D.cosA=
3.如图所示,OP是∠AOC的平分线,点B在OP上,于点D,,点B到OA的距离为2,则AB长为(
)
A.2
B.
C.
D.3
4.在△ABC中,∠C=90°,sinB=,b=,则a等于(
)
A.
B.1
C.2
D.3
5.如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
A.270cm
B.210cm
C.180cm
D.96cm
6.在中,已知∠C=90°,∠A=40°,AC=3,则BC的长为( )
A.3sin40°
B.3sin50°
C.3tan40°
D.3tan50°
7.如图,点E从点A出发沿AB方向运动,点G从点B出发沿BC方向运动,同时出发且速度相同,DE=GF
B.一直不变
C.先减小后增大
D.先增大后减小
8.如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若千米,则点两点的距离为()千米.
A.4
B.
C.2
D.6
9.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CE平分∠ACB交AB于点E.EF⊥BC于点F,若EF=4,则线段AE的长为(
)
A.2
B.
C.2+2
D.3
10.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AEFG,则图中阴影部分的面积为(
)
A.
B.
C.1-
D.1-
11.如图,嘉琪在一座桥的附近试飞一架小型无人机,为了测量无人机飞行的高度,嘉琪通过操控装置测得无人机俯视桥头,的俯角分别为和,且,,在同一水平线上,已知桥米,则无人机的飞行高度(
)
A.15米
B.米
C.米
D.米
12.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米
B.200米
C.220米
D.100米
13.如图,学校某数学兴趣小组想测量操场对面旗杆的高度,他们在C点测得旗杆顶部A的仰角为35°,再沿着坡度为3:4的楼梯向下走了3.5米到达D处,再继续向旗杆方向走了15米到达E处,在E处测得旗杆顶部A的仰角为65°,己知旗杆所在平台的高度为3.5米,则旗杆的高度为(
)(结果精确到0.1,参考数据:,).
A.19.8米
B.19.7米
C.18.3米
D.16.2米
14.如图所示,把多块大小不同的30°角三角板,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与x轴重合且点A的坐标为(2,0),∠ABO=30°,第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交x轴于点B1,第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交y轴于点B2,第四块三角板斜边B2B3与第三块三角板的斜边B1B2垂直且交x轴于点B3.按此规律继续下去,则线段OB2020的长为( )
A.2×()2020
B.2×()2021
C.()2020
D.()2021
二、填空题
15.如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为
米.
16.如图,为测量一座大厦AB的高度,当小明在C处时测得楼顶A的仰角为60°,接着沿BC方向行走30
m至D处时测得楼顶A的仰角为30°,
则大厦AB的高度是_______.
17.在△ABC中,(2sinA﹣1)2+=0,则△ABC的形状为________
18.知在中,AB=
AC=5,BC=6,则tanB的值为_____.
三、解答题
19.数学课外学习小组利用矩形建筑物ABED测量广场灯塔CF的高,如图所示,在点B处测得灯塔顶端C的仰角为28°,在点D处测得灯塔顶端C的仰角为45°,已知AB=10m,AD=30m.求灯塔CF的高(结果保留整数).
(参考数据:tan28°≈0.53,
cos28°≈0.88,sin28°≈0.47,≈1.41)
20.根据下列条件,解直角三角形
:
(1)在Rt△ABC中,∠C=90°,.
(2)在Rt△ABC中,∠C=90°,∠A=60°,c=6.
21.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
22.如图,四边形ABCD是矩形,以点A为圆心、AD为半径画弧交BC于
点E.DF⊥AE于F.若E恰好为BC的中点.
⑴
∠BAE=
°;
⑵
DF平分AE吗?证明你的结论.
23.如图,在边长为1个单位长度的小正方形组成的12×12的网格中,AB是以网络线的交点(格点)为端点的线段;
(1)将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段CD;
(2)以线段CD为一边,作一个菱形CDEF,连接DF,使,点E,F也为格点.
24.如图,052D型驱逐舰“昆明舰”执行任务后正返回葫芦岛军港C,途经渤海海域A处时,葫芦岛军港C的中国海军发现点A在南偏东30°方向上,旅顺军港B的中国海军发现点A在正西方向上.已知军港C在军港B的北偏西60°方向,且B、C两地相距120海里,(计算结果保留根号)
(1)求出此时点A到军港C的距离;
(2)若“昆明舰”从A处沿AC方向向军港C驶去,当到达A'时,测得军港B在A'的南偏东75°的方向上,求此时“昆明舰”的航行距离.
25.某“综合与实践”小组开展了测量本校对面山上一座古塔高度的实活动,他们制订了方案,并利用课余时间完成了实地测量.他们在该山脚的一块平地上,选择两个不同测点,分别测量山顶和塔顶的俯角,以及这两个测点之间的距离.为了减小测量误差,小组在测量俯角的度数以及两个测点之间的距离时,都分别测量了三次并取它们的平均值为测量结果,测量数据如下表(不完整).
课题
测量山上塔的高度
测量工具
测量角度的仪器,皮尺等
测量示意图
说明:线段表示山高,表示塔的高,测量角度的仪器的高度,端点B,C,D,A,E在同一竖直平面内,点D,C,B共线,点D,A,E共线.
测量数据
测量项目
第一次
第二次
第三次
平均值
的度数
63.6°
63.3°
63.3°
63.4°
的度数
29.9°
29.8°
30.3°
30°
的度数
44.9°
45.3°
44.8°
__________
A,E之间的距离
50.1m
49.8m
50.1m
__________
…
…
任务一:三次测量的度数平均值是__________;A,E之间的距离的平均值是__________m.
任务二,根据以上测量结果,请你帮助该“综合与实践”小组求出塔的高度.
(结果精确到0.1m.参考数据:,,,,)
26.阅读下列材料,并解决问题.
如图1,在锐角△ABC中,∠A,∠B,∠C的对边分别是a,b,c,过点A作AD⊥BC于点D,则,,即,,于是,即.
同理有:,,所以.即在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论就可以求出其余三个未知元素.
(1)如图2,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮距灯塔A的距离AB.
(2)在(1)的条件下,试求75°的正弦值.(结果保留根号)
答案
一、选择题
1.C.2.A.3.C.4.B.5.B.6.C.7.B.8.D.9.B.10.D.
11.B.12.D.13.C.14.B
二、填空题
15.
16.15
17.直角三角形.
18..
三、解答题
19.解:延长BE交CD于点G,交CF于点H,
在Rt中,∠EDG=45°,
∴EG=DE=10m.∠EGD=45°
设CH=xm,
在Rt中,∠EGD=45°,
∴GH=xm
在Rt中,∠CBH=28°,
∴tan∠CBH=,
即:=tan28°
解这个方程得:x≈45.1,
经检验:x≈45.1符合题意.
∴灯塔的高CF=55.1≈55(m)
答:灯塔的高为55米.
20.(1)∵在Rt△ABC中.∠C=90°,,
∴c===4,
∴c=2b,∠C=90°,
∴∠B=30°.
∴∠A=90°-30°=60°,
即:c=4,∠B=30°,∠A=60°;
(2)∵在Rt△ABC中.∠C=90°,∠A=60°,c=6,
∴∠B=∠C?∠A=90°?60°=30°.
∴c=2b.
∴b=3,
∴a===.
即a=,b=3,∠B=30°.
21.解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
22.解:(1)是以点A为圆心、AD为半径画弧得到的
四边形ABCD是矩形
点E恰好为BC的中点
(2)DF平分AE.
如图,连接DE
由(1)知,,
是等边三角形
所以DF平分AE.
23.(1)如图所示:线段CD即为所求;
(2)如图所示:菱形CDEF即为所求.
24.
解:(1)延长BA,过点C作CD⊥BA延长线于点D
由题意可得:∠CBD,BC=120
则DC=60
故
解得:AC=
答:此时点A到军港C的距离为海里;
(2)过点A'作A'N⊥BC于点N
可得∠1=,∠BA'A=
则∠2=,即A'B平分∠CBA
设AA'=x,则A'E=
故CA'=2A'N=
∵
∴
答:此时“昆明舰”的航行距离为海里.
25.解:任务一:∠BED的度数平均值==45?,A,E之间的距离的平均值==50,
任务一:45°;50.
任务二:∵在中,,
∴
∴①.
∵在中,,
∴,BD=2AD②,
由①与②得50+AD=2AD,AD=50,
∴ED=BD=100,
∵在中,,
∴
∴.
BC=BD-CD=100-.
∴.
答:塔的高度约为42.3m.
26.1)由题意得BC=60×0.5=30(海里),
∵CD∥BE,∠DCB=30°,
∴∠CBE=180°-∠DCB=150°,
∵∠ABE=75°,
∴∠ABC=150°-75°=75°,
∴∠A=180°-∠ABC-∠ACB=45°,
解得(海里)
所以货轮距灯塔A的距离AB为海里;
(2)过点B作BM⊥AC,在Rt△ABM中,∠A=45°,AB=,
∵,即,
∴AM=15,
在Rt△BMC中,∠BCM=60°,BC=30,则CM=BC(海里)
∴AC=AM+CM=()(海里)
∵
∴,
解得.
