北师大版九年级数学下册一课一练试题:1.1 《锐角三角函数及计算》习题(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册一课一练试题:1.1 《锐角三角函数及计算》习题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 380.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 00:00:00 | ||
图片预览




文档简介
《锐角三角函数及计算》习题
一、选择题
1.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=(
)
A.
B.
C.
D.
2.已知在Rt△ABC中,∠C=90°,sinA=,则∠A的正切值为( )
A.
B.
C.
D.
3.计算的值等于(
)
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,sinA=,那么tanB的值是( )
A.
B.
C.
D.
5.小明沿着与地面成30?的坡面向下走了2米,那么他下降(???)
A.1米
B.米
C.2米
D.米
6.在Rt△ABC中,∠ACB=90°,AB=,tan∠B=2,则AC的长为
( )
A.1
B.2
C.
D.2
7.正比例函数的图像如图所示,则的正弦值为(
)
A.
B.
C.
D.3
8.下列计算错误的是( )
A.
B.
C.
D.
9.如图,已知某广场菱形花坛的周长是24米,,则花坛对角线的长等于(
)
A.米
B.6米
C.米
D.3米
10.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.(
,1)
B.(1,
)
C.(
+1,1)
D.(1,+1)
11.在△ABC中,若,则∠C的度数是(
)
A.45°
B.60°
C.75°
D.105°
12.如图,点在正方形的边上,若,,则为( )
A.
B.2
C.
D.
13.如图,在平行四边形中,,,以点为圆心,适当的长为半径作弧,分别交于点,再分别以点为圆心,大于的长为半径作弧,两弧在内交于点,作射线交于点,交于点,则的长为(
)
A.
B.
C.
D.
14.在平面直角坐标系中,边长为的正方形的两顶点分别在轴、轴的正半轴上,点在原点.现将正方形绕点顺时针旋转,
与轴相交于点,如图,当时,点的坐标为(
)
A.
B.
C.
D.
二、填空题
15.已知中,则边的长度为____________.
16.已知a为锐角,tan(90°﹣a)=,则a的度数为________.
17.一个三角形三个内角的度数之比为1:2:3,则最小角的正弦值是_______.
18.如图,在中,点是的黄金分割点(),,如果,那么____________.
三、解答题
19.如图是直线的图像,求锐角的三个三角函数值.
20.计算:
(1).
(2).
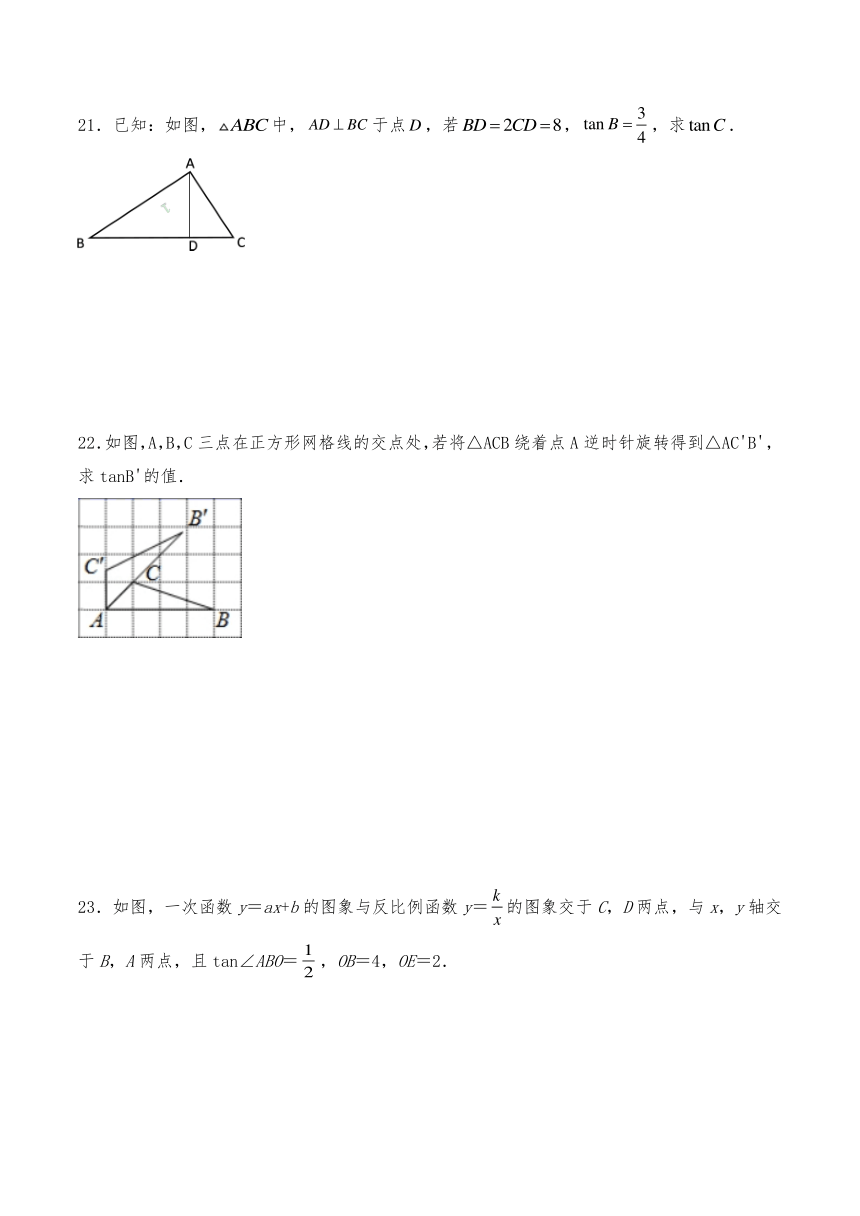
21.已知:如图,中,于点,若,,求.
22.如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC'B',求tanB'的值.
23.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积.
24.(2020·湖北孝感·初三其他)如图,射线OA放置在4×5的正方形虚线网格中,现请你在图中找出格点(即每个小正方形的顶点)B,并连接OB、AB使△AOB为直角三角形,并且
(1)使tan∠AOB的值为1;
(2)使tan∠AOB的值为.
25.(2020·遵义市第十六中学初三其他)如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.
(1)求证:四边形ADCE是矩形;
(2)若CD=1,AD=2,求sin∠COD的值.
26.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G连接DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求sin∠BAF的值.
答案
一、选择题
1.D.2.D.3.D.4.A.5.A6.B.7.B.8.
A.9.B.
10.C.11.D.12.D.13.B.14.C
二、填空题
15.4
16.30°
17.
18.
三、解答题
19.解:如图,
直线的图象与x轴的交点A为(,0),即OA=;
与y轴的交点B为(0,5),即OB=5;
则AB==;
===,
,
.
20.(1)原式
.
(2)原式
.
21.解:∵
∴CD=4
∵
∴
∴AD=BD=6
∴tanC=
22.解:根据旋转的性质可得:∠B=∠B′,
∴tanB'=tanB.
∵tanB=,
∴tanB'=.
23.解:(1)∵OB=4,OE=2,
∴BE=2+4=6,
∵CE⊥x轴于点E,tan∠ABO=,
∴OA=2,CE=3,
∴点A的坐标为(0,2)、点B的坐标为(4,0)、点C的坐标为(﹣2,3),
∵一次函数y=ax+b的图象与x,y轴交于B,A两点,
∴,
解得,
故直线AB的解析式为y=x+2,
∵反比例函数y=的图象过点C,
∴,
∴k=﹣6,
∴该反比例函数的解析式为;
(2)联立反比例函数的解析式和直线AB的解析式可得:
,解得:,
可得交点D的坐标为(6,﹣1),
则△BOD的面积为4×1÷2=2,
△BOC的面积为4×3÷2=6,
故△OCD的面积为2+6=8.
24.如图1所示:
∵OA=,且tan∠AOB=1,∴AB=OB=,∴可找到格点B.
如图2所示;
同上一问的解法,可以求得AB=,OB=.即可找到点B.
25.(1)证明:由已知得BD//CE,BD=CE,
∵CD垂直平分AB,
∴AD=BD,∠CDA=90°,
∵结合平移的性质得到:AD//CE,AD=CE,
∴四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形;
(2)解:过D作DF⊥AC于F,
在Rt△ADC中,∠CDA=90°,
∵CD=1,AD=2,
由勾股定理可得:AC=,
∵O为AC中点,
∴OD=,
∵AC?DF=AD?DC,
∴DF=,
在Rt△ODF中,∠OFD=90°,
∴sin∠COD=.
26.(1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,
∵FG∥CD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴FG=FE,
∴DG=GF=EF=DE,
∴四边形DEFG为菱形;
(2)
CD=8,CF=4,矩形
设
则
由对折可得:
由
解得:
一、选择题
1.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=(
)
A.
B.
C.
D.
2.已知在Rt△ABC中,∠C=90°,sinA=,则∠A的正切值为( )
A.
B.
C.
D.
3.计算的值等于(
)
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,sinA=,那么tanB的值是( )
A.
B.
C.
D.
5.小明沿着与地面成30?的坡面向下走了2米,那么他下降(???)
A.1米
B.米
C.2米
D.米
6.在Rt△ABC中,∠ACB=90°,AB=,tan∠B=2,则AC的长为
( )
A.1
B.2
C.
D.2
7.正比例函数的图像如图所示,则的正弦值为(
)
A.
B.
C.
D.3
8.下列计算错误的是( )
A.
B.
C.
D.
9.如图,已知某广场菱形花坛的周长是24米,,则花坛对角线的长等于(
)
A.米
B.6米
C.米
D.3米
10.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.(
,1)
B.(1,
)
C.(
+1,1)
D.(1,+1)
11.在△ABC中,若,则∠C的度数是(
)
A.45°
B.60°
C.75°
D.105°
12.如图,点在正方形的边上,若,,则为( )
A.
B.2
C.
D.
13.如图,在平行四边形中,,,以点为圆心,适当的长为半径作弧,分别交于点,再分别以点为圆心,大于的长为半径作弧,两弧在内交于点,作射线交于点,交于点,则的长为(
)
A.
B.
C.
D.
14.在平面直角坐标系中,边长为的正方形的两顶点分别在轴、轴的正半轴上,点在原点.现将正方形绕点顺时针旋转,
与轴相交于点,如图,当时,点的坐标为(
)
A.
B.
C.
D.
二、填空题
15.已知中,则边的长度为____________.
16.已知a为锐角,tan(90°﹣a)=,则a的度数为________.
17.一个三角形三个内角的度数之比为1:2:3,则最小角的正弦值是_______.
18.如图,在中,点是的黄金分割点(),,如果,那么____________.
三、解答题
19.如图是直线的图像,求锐角的三个三角函数值.
20.计算:
(1).
(2).
21.已知:如图,中,于点,若,,求.
22.如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC'B',求tanB'的值.
23.如图,一次函数y=ax+b的图象与反比例函数y=的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积.
24.(2020·湖北孝感·初三其他)如图,射线OA放置在4×5的正方形虚线网格中,现请你在图中找出格点(即每个小正方形的顶点)B,并连接OB、AB使△AOB为直角三角形,并且
(1)使tan∠AOB的值为1;
(2)使tan∠AOB的值为.
25.(2020·遵义市第十六中学初三其他)如图,CD垂直平分AB于点D,连接CA,CB,将BC沿BA的方向平移,得到线段DE,交AC于点O,连接EA,EC.
(1)求证:四边形ADCE是矩形;
(2)若CD=1,AD=2,求sin∠COD的值.
26.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G连接DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求sin∠BAF的值.
答案
一、选择题
1.D.2.D.3.D.4.A.5.A6.B.7.B.8.
A.9.B.
10.C.11.D.12.D.13.B.14.C
二、填空题
15.4
16.30°
17.
18.
三、解答题
19.解:如图,
直线的图象与x轴的交点A为(,0),即OA=;
与y轴的交点B为(0,5),即OB=5;
则AB==;
===,
,
.
20.(1)原式
.
(2)原式
.
21.解:∵
∴CD=4
∵
∴
∴AD=BD=6
∴tanC=
22.解:根据旋转的性质可得:∠B=∠B′,
∴tanB'=tanB.
∵tanB=,
∴tanB'=.
23.解:(1)∵OB=4,OE=2,
∴BE=2+4=6,
∵CE⊥x轴于点E,tan∠ABO=,
∴OA=2,CE=3,
∴点A的坐标为(0,2)、点B的坐标为(4,0)、点C的坐标为(﹣2,3),
∵一次函数y=ax+b的图象与x,y轴交于B,A两点,
∴,
解得,
故直线AB的解析式为y=x+2,
∵反比例函数y=的图象过点C,
∴,
∴k=﹣6,
∴该反比例函数的解析式为;
(2)联立反比例函数的解析式和直线AB的解析式可得:
,解得:,
可得交点D的坐标为(6,﹣1),
则△BOD的面积为4×1÷2=2,
△BOC的面积为4×3÷2=6,
故△OCD的面积为2+6=8.
24.如图1所示:
∵OA=,且tan∠AOB=1,∴AB=OB=,∴可找到格点B.
如图2所示;
同上一问的解法,可以求得AB=,OB=.即可找到点B.
25.(1)证明:由已知得BD//CE,BD=CE,
∵CD垂直平分AB,
∴AD=BD,∠CDA=90°,
∵结合平移的性质得到:AD//CE,AD=CE,
∴四边形ADCE是平行四边形,
∴平行四边形ADCE是矩形;
(2)解:过D作DF⊥AC于F,
在Rt△ADC中,∠CDA=90°,
∵CD=1,AD=2,
由勾股定理可得:AC=,
∵O为AC中点,
∴OD=,
∵AC?DF=AD?DC,
∴DF=,
在Rt△ODF中,∠OFD=90°,
∴sin∠COD=.
26.(1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,
∵FG∥CD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴FG=FE,
∴DG=GF=EF=DE,
∴四边形DEFG为菱形;
(2)
CD=8,CF=4,矩形
设
则
由对折可得:
由
解得:
