北师大版九年级数学下册一课一练试题 2.5 《二次函数与一元二次方程》习题2(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册一课一练试题 2.5 《二次函数与一元二次方程》习题2(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 557.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 17:16:55 | ||
图片预览



文档简介
2.5
《二次函数与一元二次方程》习题2
一、选择题
1.抛物线经过第四象限的点),则关于x的方程的根的情况是(
)
A.有两个大于1的不相等实数根
B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根
D.没有实数根
2.已知二次函数(其中x是自变量)的图象经过不同两点,,且该二次函数的图象与x轴有公共点,则的值(
)
A.
B.2
C.3
D.4
3.抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1,0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是(
)
A.方程ax2+bx+c=2的一个根是x=﹣2
B.若x1=2,则抛物线与x轴的另一个交点为(﹣4,0)
C.若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2
D.若≤x≤0时,2≤y≤3,则a=
4.已知函数y=﹣3﹣(x﹣m)(x﹣n),并且a,b是方程﹣3﹣(x﹣m)(x﹣n)=0的两个根,则实数m,n,a,b的大小关系可能是( ).
A.m<n<b<a
B.a<m<n<b
C.a<m<b<n
D.m<a<b<n
5.在平面直角坐标系中,抛物线与轴交于点(点在点的左侧),与轴交于点.垂直于轴的直线与抛物线交于点,,与直线交于点,若,记,则的取值范围为(
)
A.5<s<6
B.6<s<7
C.7<s<8
D.8<s<9
6.如图,抛物线与轴交于点,顶点坐标,则下列结论:
①,,;②;③关于的方程有两个不相等的实数根;④.其中结论正确的是(
)
A.①
B.②③
C.②④
D.②③④
7.二次函数y=ax2+bx+c的图像如图所示,当函数值y<0时,x的取值范围为
(
)
x<—1或x>3
B.—1<x<3
C.x≤—1或x≥3
D.—1≤x≤3
8.若关于x的方程|ax2+bx+c|=5有三个不相等的实数根,则二次函数y=ax2+bx+c有(
)
A.最小值为5
B.最大值为5
C.最大值为5或最小值-5
D.最大值-5或最小值5
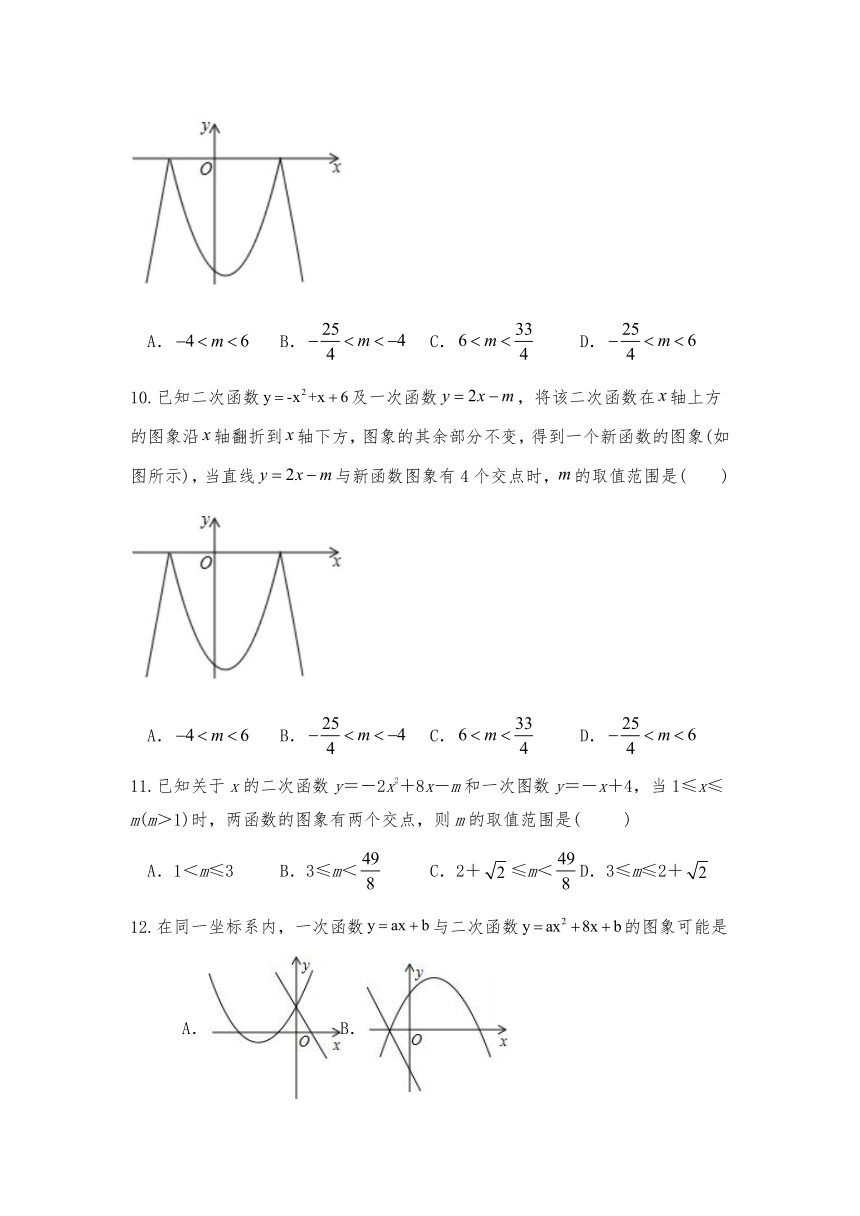
9.已知二次函数及一次函数,将该二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线与新函数图象有4个交点时,的取值范围是( )
A.
B.
C.
D.
10.已知二次函数及一次函数,将该二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线与新函数图象有4个交点时,的取值范围是( )
A.
B.
C.
D.
11.已知关于x的二次函数y=-2x2+8x-m和一次图数y=-x+4,当1≤x≤m(m>1)时,两函数的图象有两个交点,则m的取值范围是(
)
A.1<m≤3
B.3≤m<
C.2+≤m<
D.3≤m≤2+
12.在同一坐标系内,一次函数与二次函数的图象可能是
A.B.
C.D.
13.如图,二次函数:与一次函数:y=mx+n(m≠0)的图象交于A,B两点,则一元二次方程的解为( )
A.
B.,
C.,
D.
二、填空题
1.已知二次函数图象上部分点的横坐标与纵坐标的对应值如下表所示,图象与轴的一个交点坐标为,那么它的图象与轴的另一个交点坐标是___________.
…
0
1
2
…
…
0
3
4
3
…
2.若x1,x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数a,b,x1,x2的大小关系为_____.
3.已知直线y=b(b为实数)与函数
y=的图像至少有三个公共点,则实数b的取值范围
.
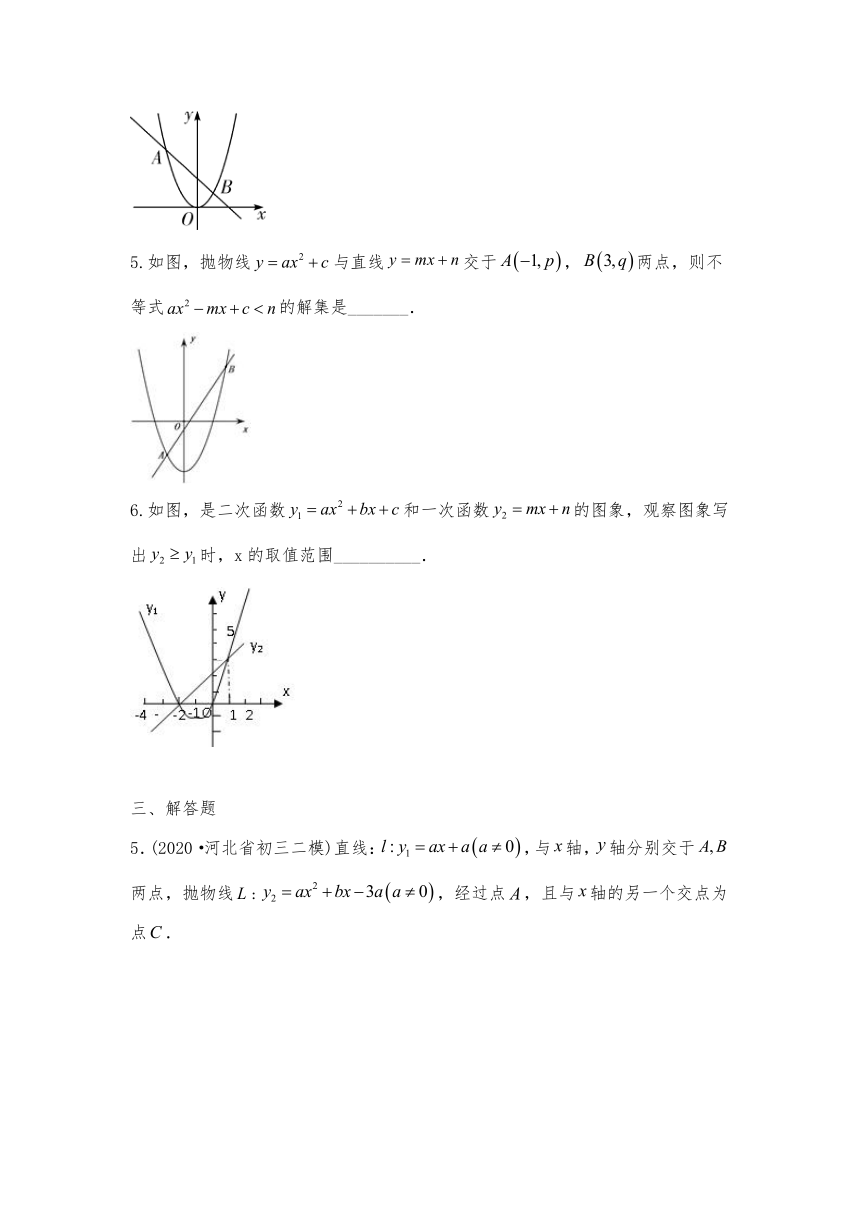
4.如图,抛物线与直线的两个交点坐标分别为,则关于x的方程的解为________.
5.如图,抛物线与直线交于,两点,则不等式的解集是_______.
6.如图,是二次函数和一次函数的图象,观察图象写出时,x的取值范围__________.
三、解答题
5.(2020·河北省初三二模)直线:,与轴,轴分别交于两点,抛物线:,经过点,且与轴的另一个交点为点.
(1)若,求此时抛物线的解析式、顶点坐标及点坐标;
(2)在直线与抛物线围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
(3)①直线与轴的交点的坐标会变吗?说明理由;
2.画出二次函数y=x2-2x的图象,利用图象回答:
(1)方程x2-2x=0的解是什么?
(2)x取什么值时,函数值大于0?
(3)x取什么值时,函数值小于0?
3.已知二次函数.
(1)求函数图象的顶点坐标,与坐标轴交点坐标,并画出函数大致图象;
(2)根据图象直接回答:当x为何值时,?当x为何值时?
4.关于x的二次函数(k为常数)和一次函数.
(1)求证:函数的图象与x轴有交点.
(2)已知函数的图象与x轴的两个交点间的距离等于3,
①试求此时k的值.
②若,试求x的取值范围.
5.已知二次函数(为常数).
(1)求证:不论为何值,该二次函数的图像与轴总有公共点.
(2)求证:不论为何值,该二次函数的图像的顶点都在函数的图像上.
(3)已知点、,线段与函数的图像有公共点,则的取值范围是__________.
6.如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
答案
一、选择题
1.C.2.C.3.D.4.D.5.C.6.B7.B.8.C.
9.C.10.C.11.D.12.C.13.C
二、填空题
1.(3,0).
2.x1<a<b<x2
3.04.
5.
6.-2≤x≤1.
三、解答题
1.解:(1)若,,当时,
∴,
将代入,可得
∴
∴顶点为
∵点,点关于对称
∴
(2)设直线与抛物线的另一个交点为,
,
解得,,所以交点为和,
所以,直线上神秘点为,,,,,共6个,
抛物线上神秘点为,,,共4个,
综上,神秘点个数为10;
(1)①不会变,,
当时,无论取何非零实数,恒为0,
所以,直线永远经过点,所以点坐标不会改变;
②,,
由①知恒过
∴过∴∴
∴
∴与轴恒交于,
对称轴为不变
∵与在有唯一公共点
∴当时过
解得
∵开口越小,越大
∴
当时
①顶点在上,顶点为
∴
②抛物线恰好过
∴
∴
综上,,时抛物线与在有唯一公共点
2.二次函数y=x2-2x的图象如下图所示:
(1)观察图象可得方程x2-2x=0的解是x1=0,x2=2;
(2)观察图象可得,当x取x<0或x>2时,函数值大于0;
(3)观察图象可得,当x取03.解:,
顶点坐标为,
当时,;
当时,,
解得:,或,
二次函数的图象与y轴的交点坐标为,与x轴的交点坐标为,;
图象如图所示:
当,;
当或,.
4.解:(1)证明:△=(2k?1)2+8
k=4k2?4k+1+8k=(2k+1)2≥0,
∴函数y1=kx2+(2k?1)
x
?
2的图象与x轴有交点.
(2)解:①设的两根为,,则,,
,
函数的图象与轴的两个交点间的距离等于3,
,
,
解得,或;
②I.当k=1时,y1=
x2+
x
–
2,画出y1=
x2+
x
–
2和y2=x+2的图象,如图1所示,
由图知,y1与y2的交点分别为(?2,0)和
(2,4),
∴当y1>y2时x<–
2或
x>2;
II.当k=时,y1=x2x
–
2,
画出y1=x2x
–
2和y2=x+2的图象,如图2所示,
由图知,y1与y2的交点分别为(?2,0)和
(?10,?8),
∴当y1>y2时?10<x<–
2.
综上所述,当k=1时x<–
2或
x>2,当k=时,?10<x<–
2.
5.(1)令,则.
∵,,,
∴.
∵,
∴.
∴一元二次方程有实数根.
故不论取何值,函数与轴总有公共点.
(2)∵.
∴该函数的顶点坐标为.
把代入,得.
∴不论为何值,该二次函数的顶点坐标都在函数上.
(3)当y=-1时,y=-(x-1)2=-1,解得x1=0,x2=2,
当a+2≥0且a≤2时,线段AB与函数y=-(x-1)2的图象有公共点,
所以a的范围为-2≤a≤2.
故答案为.
6.(1)抛物线的对称轴为:.
∴,抛物线开口向上,大致图象如图所示.
当时,随增大而增大;
∵当时,函数有最大值,
∴当时,,
∴,
解得:.
∴
当,,
,x2-2x-3=0,
解得:或,
∴抛物线与轴交于,抛物线与轴交于,.
(2)∵关于的一元二次方程恒有实数根,
∴,即恒成立,
∴恒成立.
∵(1)中的抛物线解析式为y=x2-2x-3,
∴函数的最小值为=-4,
∵点是(1)中抛物线沿x轴翻折得到的抛物线弧部分上任意一点,
∴,
∴(k取值的下限),
∴实数的最大值为3.
《二次函数与一元二次方程》习题2
一、选择题
1.抛物线经过第四象限的点),则关于x的方程的根的情况是(
)
A.有两个大于1的不相等实数根
B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根
D.没有实数根
2.已知二次函数(其中x是自变量)的图象经过不同两点,,且该二次函数的图象与x轴有公共点,则的值(
)
A.
B.2
C.3
D.4
3.抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过点(0,2),且关于直线x=﹣1对称,(x1,0)是抛物线与x轴的一个交点,有下列结论,其中结论错误的是(
)
A.方程ax2+bx+c=2的一个根是x=﹣2
B.若x1=2,则抛物线与x轴的另一个交点为(﹣4,0)
C.若m=4时,方程ax2+bx+c=m有两个相等的实数根,则a=﹣2
D.若≤x≤0时,2≤y≤3,则a=
4.已知函数y=﹣3﹣(x﹣m)(x﹣n),并且a,b是方程﹣3﹣(x﹣m)(x﹣n)=0的两个根,则实数m,n,a,b的大小关系可能是( ).
A.m<n<b<a
B.a<m<n<b
C.a<m<b<n
D.m<a<b<n
5.在平面直角坐标系中,抛物线与轴交于点(点在点的左侧),与轴交于点.垂直于轴的直线与抛物线交于点,,与直线交于点,若,记,则的取值范围为(
)
A.5<s<6
B.6<s<7
C.7<s<8
D.8<s<9
6.如图,抛物线与轴交于点,顶点坐标,则下列结论:
①,,;②;③关于的方程有两个不相等的实数根;④.其中结论正确的是(
)
A.①
B.②③
C.②④
D.②③④
7.二次函数y=ax2+bx+c的图像如图所示,当函数值y<0时,x的取值范围为
(
)
x<—1或x>3
B.—1<x<3
C.x≤—1或x≥3
D.—1≤x≤3
8.若关于x的方程|ax2+bx+c|=5有三个不相等的实数根,则二次函数y=ax2+bx+c有(
)
A.最小值为5
B.最大值为5
C.最大值为5或最小值-5
D.最大值-5或最小值5
9.已知二次函数及一次函数,将该二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线与新函数图象有4个交点时,的取值范围是( )
A.
B.
C.
D.
10.已知二次函数及一次函数,将该二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线与新函数图象有4个交点时,的取值范围是( )
A.
B.
C.
D.
11.已知关于x的二次函数y=-2x2+8x-m和一次图数y=-x+4,当1≤x≤m(m>1)时,两函数的图象有两个交点,则m的取值范围是(
)
A.1<m≤3
B.3≤m<
C.2+≤m<
D.3≤m≤2+
12.在同一坐标系内,一次函数与二次函数的图象可能是
A.B.
C.D.
13.如图,二次函数:与一次函数:y=mx+n(m≠0)的图象交于A,B两点,则一元二次方程的解为( )
A.
B.,
C.,
D.
二、填空题
1.已知二次函数图象上部分点的横坐标与纵坐标的对应值如下表所示,图象与轴的一个交点坐标为,那么它的图象与轴的另一个交点坐标是___________.
…
0
1
2
…
…
0
3
4
3
…
2.若x1,x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数a,b,x1,x2的大小关系为_____.
3.已知直线y=b(b为实数)与函数
y=的图像至少有三个公共点,则实数b的取值范围
.
4.如图,抛物线与直线的两个交点坐标分别为,则关于x的方程的解为________.
5.如图,抛物线与直线交于,两点,则不等式的解集是_______.
6.如图,是二次函数和一次函数的图象,观察图象写出时,x的取值范围__________.
三、解答题
5.(2020·河北省初三二模)直线:,与轴,轴分别交于两点,抛物线:,经过点,且与轴的另一个交点为点.
(1)若,求此时抛物线的解析式、顶点坐标及点坐标;
(2)在直线与抛物线围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
(3)①直线与轴的交点的坐标会变吗?说明理由;
2.画出二次函数y=x2-2x的图象,利用图象回答:
(1)方程x2-2x=0的解是什么?
(2)x取什么值时,函数值大于0?
(3)x取什么值时,函数值小于0?
3.已知二次函数.
(1)求函数图象的顶点坐标,与坐标轴交点坐标,并画出函数大致图象;
(2)根据图象直接回答:当x为何值时,?当x为何值时?
4.关于x的二次函数(k为常数)和一次函数.
(1)求证:函数的图象与x轴有交点.
(2)已知函数的图象与x轴的两个交点间的距离等于3,
①试求此时k的值.
②若,试求x的取值范围.
5.已知二次函数(为常数).
(1)求证:不论为何值,该二次函数的图像与轴总有公共点.
(2)求证:不论为何值,该二次函数的图像的顶点都在函数的图像上.
(3)已知点、,线段与函数的图像有公共点,则的取值范围是__________.
6.如图,直线y=x+m与二次函数y=ax2+2x+c的图象交于点A(0,3),已知该二次函数图象的对称轴为直线x=1.
(1)求m的值及二次函数解析式;
(2)若直线y=x+m与二次函数y=ax2+2x+c的图象的另一个交点为B,求△OAB的面积;
(3)根据函数图象回答:x为何值时该一次函数值大于二次函数值.
答案
一、选择题
1.C.2.C.3.D.4.D.5.C.6.B7.B.8.C.
9.C.10.C.11.D.12.C.13.C
二、填空题
1.(3,0).
2.x1<a<b<x2
3.0
5.
6.-2≤x≤1.
三、解答题
1.解:(1)若,,当时,
∴,
将代入,可得
∴
∴顶点为
∵点,点关于对称
∴
(2)设直线与抛物线的另一个交点为,
,
解得,,所以交点为和,
所以,直线上神秘点为,,,,,共6个,
抛物线上神秘点为,,,共4个,
综上,神秘点个数为10;
(1)①不会变,,
当时,无论取何非零实数,恒为0,
所以,直线永远经过点,所以点坐标不会改变;
②,,
由①知恒过
∴过∴∴
∴
∴与轴恒交于,
对称轴为不变
∵与在有唯一公共点
∴当时过
解得
∵开口越小,越大
∴
当时
①顶点在上,顶点为
∴
②抛物线恰好过
∴
∴
综上,,时抛物线与在有唯一公共点
2.二次函数y=x2-2x的图象如下图所示:
(1)观察图象可得方程x2-2x=0的解是x1=0,x2=2;
(2)观察图象可得,当x取x<0或x>2时,函数值大于0;
(3)观察图象可得,当x取0
顶点坐标为,
当时,;
当时,,
解得:,或,
二次函数的图象与y轴的交点坐标为,与x轴的交点坐标为,;
图象如图所示:
当,;
当或,.
4.解:(1)证明:△=(2k?1)2+8
k=4k2?4k+1+8k=(2k+1)2≥0,
∴函数y1=kx2+(2k?1)
x
?
2的图象与x轴有交点.
(2)解:①设的两根为,,则,,
,
函数的图象与轴的两个交点间的距离等于3,
,
,
解得,或;
②I.当k=1时,y1=
x2+
x
–
2,画出y1=
x2+
x
–
2和y2=x+2的图象,如图1所示,
由图知,y1与y2的交点分别为(?2,0)和
(2,4),
∴当y1>y2时x<–
2或
x>2;
II.当k=时,y1=x2x
–
2,
画出y1=x2x
–
2和y2=x+2的图象,如图2所示,
由图知,y1与y2的交点分别为(?2,0)和
(?10,?8),
∴当y1>y2时?10<x<–
2.
综上所述,当k=1时x<–
2或
x>2,当k=时,?10<x<–
2.
5.(1)令,则.
∵,,,
∴.
∵,
∴.
∴一元二次方程有实数根.
故不论取何值,函数与轴总有公共点.
(2)∵.
∴该函数的顶点坐标为.
把代入,得.
∴不论为何值,该二次函数的顶点坐标都在函数上.
(3)当y=-1时,y=-(x-1)2=-1,解得x1=0,x2=2,
当a+2≥0且a≤2时,线段AB与函数y=-(x-1)2的图象有公共点,
所以a的范围为-2≤a≤2.
故答案为.
6.(1)抛物线的对称轴为:.
∴,抛物线开口向上,大致图象如图所示.
当时,随增大而增大;
∵当时,函数有最大值,
∴当时,,
∴,
解得:.
∴
当,,
,x2-2x-3=0,
解得:或,
∴抛物线与轴交于,抛物线与轴交于,.
(2)∵关于的一元二次方程恒有实数根,
∴,即恒成立,
∴恒成立.
∵(1)中的抛物线解析式为y=x2-2x-3,
∴函数的最小值为=-4,
∵点是(1)中抛物线沿x轴翻折得到的抛物线弧部分上任意一点,
∴,
∴(k取值的下限),
∴实数的最大值为3.
