2013高三第一轮复习课件:第一讲:集合与简易逻辑
文档属性
| 名称 | 2013高三第一轮复习课件:第一讲:集合与简易逻辑 |  | |
| 格式 | zip | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-01 16:02:46 | ||
图片预览








文档简介
(共26张PPT)
第一讲 集合与常用逻辑用语
主干知识整合
1.集合中的元素具有的三个特征
(1)确定性;(2)互异性;(3)无序性.
2.集合的三种运算
(1)并集:A∪B={x|x∈A或x∈B};
(2)交集:A∩B={x|x∈A且x∈B};
(3)补集: UA={x|x∈U,且x A}.
3.四种命题的真假关系
(1)两个命题互为逆否命题时,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.
4.充分条件、必要条件、充要条件
对于“若p则q”形式的命题
(1)若p q成立,则p是q的充分条件,q是p的必要条件;
(2)若p q,且q / p,则p是q的充分不必要条件;
(3)若p q且q p,则p是q的充要条件.
5.命题p∧q,p∨q及綈p真假的判定
p q 綈p p∨q p∧q
真 真 假 真 真
真 假 假 真 假
假 真 真 真 假
假 假 真 假 假
6.含有一个量词的命题的否定
(1)全称命题p: x∈M,p(x),它的否定 p: x0∈M, p(x0);
(2)特称命题(存在性命题)p: x0∈M,p(x0),它的否定 p: x∈M, p(x).
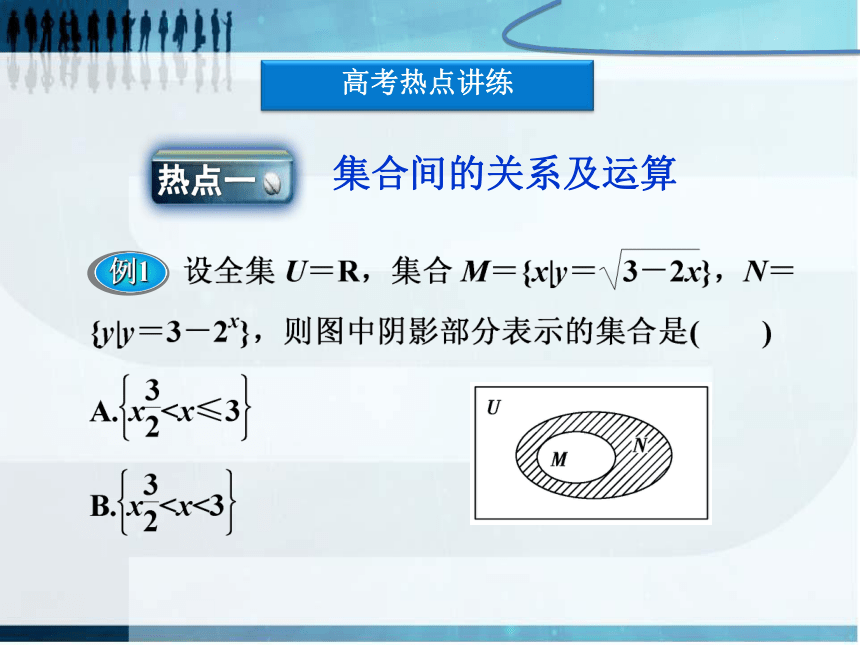
高考热点讲练
集合间的关系及运算
例1
【答案】 B
【归纳拓展】 解答集合间关系与运算问题的一般步骤:先正确理解各个集合的含义,认清集合元素的属性;再依据元素的不同属性采用不同的方法对集合进行化简求解,一般的规律为:
(1)若给定的集合是不等式的解集,用数轴求解;
(2)若给定的集合是点集,用数形结合法求解;
(3)若给定的集合是抽象集合,用Venn图求解.
变式训练1 设全集U=A∪B={x∈N*|lg x<1},若A∩( UB)={m|m=2n+1,n=0,1,2,3,4},则集合B=________.
解析:A∪B={x∈N*|lg x<1}={1,2,3,4,5,6,7,8,9},A∩( UB)={m|m=2n+1,n=0,1,2,3,4}={1,3,5,7,9},∴B={2,4,6,8}.
答案:{2,4,6,8}
下列四个命题:
①命题“若a=0,则ab=0”的否命题是“若a=0,则ab≠0”;
②若命题p: x∈R,x2+x+1<0,则綈p: x∈R,x2+x+1≥0;
③若命题“綈p”与命题“p或q”都是真命题,则命题q一定是真命题;
四种命题及其相互关系
例2
【解析】 对于①,原命题的否命题是“若a≠0,则ab≠0”,所以①错;易知②正确;对于③,命题“綈p”是真命题,则命题p是假命题,
【答案】 ②③
【归纳拓展】 命题真假的判定方法:
(1)一般命题p的真假由涉及到的相关交汇知识辨别真假.
(2)四种命题的真假的判断根据:一个命题和它的逆否命题同真假,而与它的其他两个命题的真假无此规律.
(3)形如p∨q、p∧q、綈p命题真假,根据真值表判定.
(4)全称命题与特称命题的真假,根据教材中给定的方法判断.
变式训练2 有下列四个命题:
(1)若“xy=1,则x,y互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若m≤1,则x2-2x+m=0有实数解”的逆否命题;
(4)“若A∩B=B,则A B”的逆否命题.
其中真命题为( )
A.(1)(2) B.(2)(3)
C.(4) D.(1)(2)(3)
解析:选D.(1)的逆命题:“若x,y互为倒数,则xy=1”是真命题;(2)的否命题:“面积不相等的三角形不是全等三角形”是真命题;(3)的逆否命题:“若x2-2x+m=0没有实数解,则m>1”是真命题;命题(4)是假命题,所以它的逆否命题也是假命题.如A={1,2,3,4,5},B={4,5},显然A B是错误的.
充要条件
例3
【答案】 A
【归纳拓展】 对充分、必要条件的判断或探求要注意以下几点:
(1)要弄清先后顺序:“A的充分不必要条件是B”是指B能推出A,且A不能推出B;而“A是B的充分不必要条件”则是指A能推出B,且B不能推出A;
(2)要善于举出反例:如果从正面判断或证明一个命题的正确或错误不易进行时,可以通过举出恰当的反例来说明;
(3)要注意转化:如果p是q的充分不必要条件,那么 p是 q的必要不充分条件,同理,如果p是q的必要不充分条件,那么綈p是綈q的充分不必要条件,如果p是q的充要条件,那么綈p是 q的充要条件.
解析:选C.对于①,易知是正确的;对于②,由“ p是q的必要条件”得知,由q可推知綈p,由p可推知 q(注:互为逆否的两个命题的真假性一致),因此p是 q的充分条件,②正确;
考题解答技法
(2012年广东调研)已知集合A={(x,y)|x,y为实数,且x2+y2=1},B={(x,y)|x,y为实数,且x+y=1},则A∩B的元素个数为( )
A.4 B.3
C.2 D.1
例
【解析】 集合A表示圆x2+y2=1上的点构成的集合,集合B表示直线x+y=1上的点构成的集合,可判断直线与圆相交,故A∩B的元素的个数为2.
【答案】 C
【得分技巧】 解答与集合有关的问题时,首先认清集合中的元素是什么?具有什么特征?属于什么类型,是数集还是点集还是图形集?然后进行相关运算,以免混淆集合中元素的属性.
【失分溯源】 本题在求解时,有的考生不明确集合中元素是数对或理解为点的坐标;在解法上利用方程组求解,相对于上述解法要麻烦一些,容易出错.
变式训练 已知集合A={y|x2+y2=1}和集合B={y|y=x2},则A∩B等于( )
A.(0,1) B.[0,1]
C.(0,+∞) D.{(0,1),(1,0)}
解析:选B.∵A={y|x2+y2=1},∴A={y|-1≤y≤1},又∵B={y|y=x2},∴B={y|y≥0},∴A∩B={y|0≤y≤1},故选B.
第一讲 集合与常用逻辑用语
主干知识整合
1.集合中的元素具有的三个特征
(1)确定性;(2)互异性;(3)无序性.
2.集合的三种运算
(1)并集:A∪B={x|x∈A或x∈B};
(2)交集:A∩B={x|x∈A且x∈B};
(3)补集: UA={x|x∈U,且x A}.
3.四种命题的真假关系
(1)两个命题互为逆否命题时,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.
4.充分条件、必要条件、充要条件
对于“若p则q”形式的命题
(1)若p q成立,则p是q的充分条件,q是p的必要条件;
(2)若p q,且q / p,则p是q的充分不必要条件;
(3)若p q且q p,则p是q的充要条件.
5.命题p∧q,p∨q及綈p真假的判定
p q 綈p p∨q p∧q
真 真 假 真 真
真 假 假 真 假
假 真 真 真 假
假 假 真 假 假
6.含有一个量词的命题的否定
(1)全称命题p: x∈M,p(x),它的否定 p: x0∈M, p(x0);
(2)特称命题(存在性命题)p: x0∈M,p(x0),它的否定 p: x∈M, p(x).
高考热点讲练
集合间的关系及运算
例1
【答案】 B
【归纳拓展】 解答集合间关系与运算问题的一般步骤:先正确理解各个集合的含义,认清集合元素的属性;再依据元素的不同属性采用不同的方法对集合进行化简求解,一般的规律为:
(1)若给定的集合是不等式的解集,用数轴求解;
(2)若给定的集合是点集,用数形结合法求解;
(3)若给定的集合是抽象集合,用Venn图求解.
变式训练1 设全集U=A∪B={x∈N*|lg x<1},若A∩( UB)={m|m=2n+1,n=0,1,2,3,4},则集合B=________.
解析:A∪B={x∈N*|lg x<1}={1,2,3,4,5,6,7,8,9},A∩( UB)={m|m=2n+1,n=0,1,2,3,4}={1,3,5,7,9},∴B={2,4,6,8}.
答案:{2,4,6,8}
下列四个命题:
①命题“若a=0,则ab=0”的否命题是“若a=0,则ab≠0”;
②若命题p: x∈R,x2+x+1<0,则綈p: x∈R,x2+x+1≥0;
③若命题“綈p”与命题“p或q”都是真命题,则命题q一定是真命题;
四种命题及其相互关系
例2
【解析】 对于①,原命题的否命题是“若a≠0,则ab≠0”,所以①错;易知②正确;对于③,命题“綈p”是真命题,则命题p是假命题,
【答案】 ②③
【归纳拓展】 命题真假的判定方法:
(1)一般命题p的真假由涉及到的相关交汇知识辨别真假.
(2)四种命题的真假的判断根据:一个命题和它的逆否命题同真假,而与它的其他两个命题的真假无此规律.
(3)形如p∨q、p∧q、綈p命题真假,根据真值表判定.
(4)全称命题与特称命题的真假,根据教材中给定的方法判断.
变式训练2 有下列四个命题:
(1)若“xy=1,则x,y互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若m≤1,则x2-2x+m=0有实数解”的逆否命题;
(4)“若A∩B=B,则A B”的逆否命题.
其中真命题为( )
A.(1)(2) B.(2)(3)
C.(4) D.(1)(2)(3)
解析:选D.(1)的逆命题:“若x,y互为倒数,则xy=1”是真命题;(2)的否命题:“面积不相等的三角形不是全等三角形”是真命题;(3)的逆否命题:“若x2-2x+m=0没有实数解,则m>1”是真命题;命题(4)是假命题,所以它的逆否命题也是假命题.如A={1,2,3,4,5},B={4,5},显然A B是错误的.
充要条件
例3
【答案】 A
【归纳拓展】 对充分、必要条件的判断或探求要注意以下几点:
(1)要弄清先后顺序:“A的充分不必要条件是B”是指B能推出A,且A不能推出B;而“A是B的充分不必要条件”则是指A能推出B,且B不能推出A;
(2)要善于举出反例:如果从正面判断或证明一个命题的正确或错误不易进行时,可以通过举出恰当的反例来说明;
(3)要注意转化:如果p是q的充分不必要条件,那么 p是 q的必要不充分条件,同理,如果p是q的必要不充分条件,那么綈p是綈q的充分不必要条件,如果p是q的充要条件,那么綈p是 q的充要条件.
解析:选C.对于①,易知是正确的;对于②,由“ p是q的必要条件”得知,由q可推知綈p,由p可推知 q(注:互为逆否的两个命题的真假性一致),因此p是 q的充分条件,②正确;
考题解答技法
(2012年广东调研)已知集合A={(x,y)|x,y为实数,且x2+y2=1},B={(x,y)|x,y为实数,且x+y=1},则A∩B的元素个数为( )
A.4 B.3
C.2 D.1
例
【解析】 集合A表示圆x2+y2=1上的点构成的集合,集合B表示直线x+y=1上的点构成的集合,可判断直线与圆相交,故A∩B的元素的个数为2.
【答案】 C
【得分技巧】 解答与集合有关的问题时,首先认清集合中的元素是什么?具有什么特征?属于什么类型,是数集还是点集还是图形集?然后进行相关运算,以免混淆集合中元素的属性.
【失分溯源】 本题在求解时,有的考生不明确集合中元素是数对或理解为点的坐标;在解法上利用方程组求解,相对于上述解法要麻烦一些,容易出错.
变式训练 已知集合A={y|x2+y2=1}和集合B={y|y=x2},则A∩B等于( )
A.(0,1) B.[0,1]
C.(0,+∞) D.{(0,1),(1,0)}
解析:选B.∵A={y|x2+y2=1},∴A={y|-1≤y≤1},又∵B={y|y=x2},∴B={y|y≥0},∴A∩B={y|0≤y≤1},故选B.
同课章节目录
