人教A版高三数学一轮复习第一章第一节集合与简易逻辑
文档属性
| 名称 | 人教A版高三数学一轮复习第一章第一节集合与简易逻辑 |  | |
| 格式 | zip | ||
| 文件大小 | 820.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-01 16:04:30 | ||
图片预览











文档简介
(共38张PPT)
第一节 集合
一、元素与集合
1.集合中元素的三个特性: 、 、 .
2.集合中元素与集合的关系.
元素与集合之间的关系有 和 两种,表示符号为 和 .
3.常见集合的符号表示.
4. 集合的表示法: 、 、 .
确定性
互异性
无序性
属于
不属于
∈
N
N*或N+
Z
Q
R
列举法
描述法
Venn图法
二、集合间的基本关系
定义 记法
集合
间的
基本
关系 相等 集合A与集合B中的所有元素都相同
子集 A中任意一元素均为B中的元素 或
真子集 A中任意一元素均为B中的元素,且B中至少有一个元素A中没有
空集 空集是任何集合的子集
空集是任何 的真子集
关系
表示
或
非空集合
A=B
A B
B A
(B≠ )
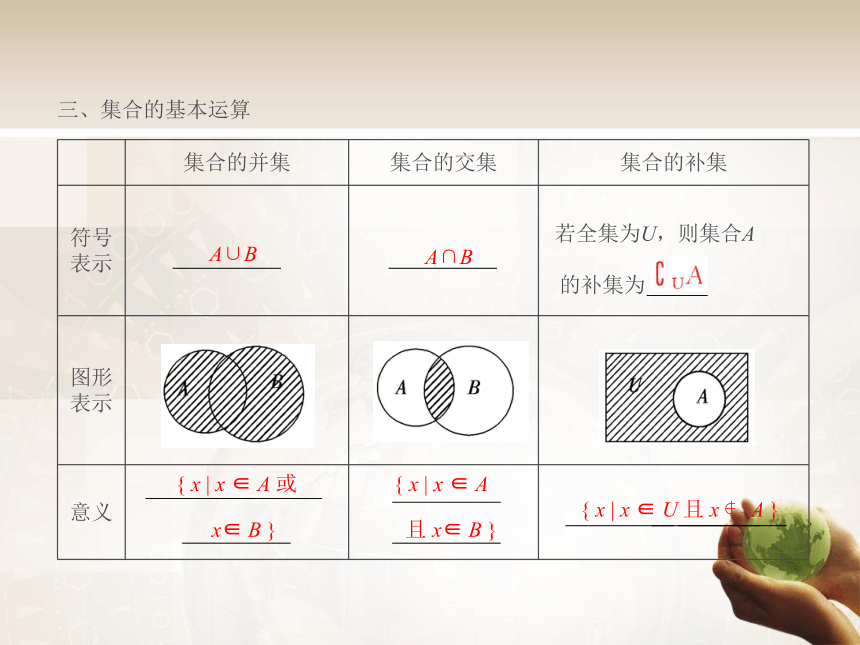
三、集合的基本运算
集合的并集 集合的交集 集合的补集
符号表示 若全集为U,则集合A
的补集为
图形表示
意义
A∪B
A∩B
{ x | x ∈ A 或
x∈ B }
且 x∈ B }
{ x | x ∈ A
{ x | x ∈ U 且 x A }
1.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦
恩(Venn)图是 ( )
2.已知集合M={0,1,2},N={x|x=2a,a∈M},则集合M∩N= ( )
A.{0} B.{0,1}
C.{1,2} D.{0,2}
【解析】 ∵M={0,1,2},N={x|x=2a,a∈M},
∴N={0,2,4},∴M∩N={0,2}.
【答案】 D
3.(2011年高考安徽卷,2)集合U={1,2,3,4,5,6},S={1,4,5},T={2,3,4},则
S∩( UT)等于 ( )
A.{1,4,5,6} B.{1,5}
C.{4} D.{1,2,3,4,5}
【解析】 S∩( UT)={1,4,5}∩{1,5,6}={1,5}.
【答案】 B
4.设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B=______.
【解析】 ∵A∩B={2},∴log2(a+3)=2.∴a=1,b=2.
∴A={5,2},B={1,2}.∴A∪B={1,2,5}.
【答案】 {1,2,5}
5.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是_____.
【解析】 借助数轴可知a≤1,如图所示.
【答案】 a≤1
考点一 集合的基本概念
1.掌握集合的概念,关键是把握集合中元素的特性,要特别注意集合中元素的
互异性,一方面利用集合元素的互异性能顺利找到解题的切入点;另一方面,
在解答完毕之时,注意检验集合的元素是否满足互异性以确保答案正确.
2.用描述法表示集合时,首先应清楚集合的类型和元素的性质.如集合{y|y=2x
},{x|y=2x},{(x,y)|y=2x}表示不同的集合.
在数集{2x,x2-x}中,实数x的取值范围是______.
【自主解答】 实数x的取值满足集合元素的互异性,则2x≠x2-x,解得x≠0
且x≠3,
∴实数x的取值范围是{x|x<0或0<x<3或x>3}.
【答案】 {x|x<0或0<x<3或x>3}
【答案】 C
考点二 集合间的基本关系
1.子集与真子集的区别与联系:集合A的真子集一定是其子集,而集合A的子集
不一定是其真子集;若集合A有n个元素,则其子集个数为2n,真子集个数为
2n-1.
2.判断集合与集合的关系,基本方法是归纳为判断元素与集合的关系.对于用
描述法表示的集合,要紧紧抓住代表元素及它的属性,可将元素列举出来直
观发现或通过元素特征,求同存异,定性分析.应做到意义化(分清集合的种
类,数集、点集、图形、定义域、值域、方程或不等式的解或解集等)、具体
化(具体求出相关的集合并化简)、直观化(借助数轴、Venn图、函数图象等,
即数形结合的思想).
已知集合A={x|x2-3x+2≤0},B={x|x2-(a+1)x+a≤0}.
(1)若A?B,求a的取值范围;
(2)若B A,求a的取值范围;
(3)若A=B,求a的取值范围.
【思路点拨】 解决本题的关键是将B集合化简,即因式分解,再根据A,B间
的关系求解.
【自主解答】 由x2-3x+2≤0,即(x-1)(x-2)≤0,
得1≤x≤2,故A={x|1≤x≤2},
而集合B={x|(x-1)(x-a)≤0},
则(1)若A是B的真子集,即A?B,
则此时B={x|1≤x≤a},故a>2.
(2)若B是A的子集,即B A,由数轴可知1≤a≤2.
(3)若A=B,则必有a=2.
2.已知集合A={x|x2-3x-10≤0},
(1)若B A,B={x|m+1≤x≤2m-1},求实数m的取值范围;
(2)若A B,B={x|m-6≤x≤2m-1},求实数m的取值范围;
(3)若A=B,B={x|m-5≤x≤2m-1},求实数m的值.
【自主解答】 (1)由A={x|x2-3x-10≤0},得
A={x|-2≤x≤5},∵B A,
∴①若B= ,则m+1>2m-1,即m<2,此时满足B A.
②若B≠ ,
考点三 集合的基本运算
在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化.一般
地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,用数轴表示时
注意端点值的取舍.
【思路点拨】 利用集合A,B的关系,借助数轴,列出关于a的不等式组求解.
(1分)
(5分)
(8分)
3.已知集合A={x|x2-6x+8<0},B={x|(x-a)(x-3a)<0}.
(1)若A B,求a的取值范围;
(2)若A∩B= ,求a的取值范围;
(3)若A∩B={x|3<x<4},求a的取值范围.
一、选择题
1.已知集合M={x |-3<x≤5},N={ x | x<-5或 x>5},则M∪N=( )
A.{x | x<-5 或 x>-3} B.{x|-5<x<5}
C.{x|-3<x<5} D.{x | x<-3或 x>5}
【解析】
由题意画出图形.可知,M∪N={x|x<-5或x>-3}.
【答案】 A
【答案】 B
3.(2011年高考广东卷,2)已知集合A={(x,y)|x,y为实数,且x2+y2=1},B=
{(x,y)|x,y为实数,且y=x},则A∩B的元素个数为 ( )
A.3 B.2
C.1 D.0
【答案】 B
4.设全集U是实数集R,M={x|x2>4},N={x|x≥3或x<1}都是U的子集,则图中
阴影部分所表示的集合是 ( )
A.{x|-2≤x<1}
B.{x|-2≤x≤2}
C.{x|1<x≤2}
D.{x|x<2}
【解析】 图中阴影部分表示N∩( UM),
∵M={|x2>4}={x|x>2或x<-2}
∴ UM={x|-2≤x≤2},
∴N∩( UM)={-2≤x<1}.
【答案】 A
【答案】 A
二、填空题
6.(2012年天津模拟)已知集合A={x∈R||x-1|<2},Z为整数集,则集合A∩Z
中所有元素的和等于________.
【解析】 A={x|-1<x<3},A∩Z={0,1,2},A∩Z中所有元素之和等于3.
【答案】 3
7.非空集合G关于运算 满足:(1)对任意a、b∈G,都有a b∈G;(2)存在e∈G,
使得对一切a∈G,都有a e=e a=a,则称G关于运算 为“融洽集”.现给
出下列集合和运算:
①G={非负整数}, 为整数的加法.
②G={偶数}, 为整数的乘法.
③G={平面向量}, 为平面向量的加法.
④G={二次三项式}, 为多项式的加法.
⑤G={虚数}, 为复数的乘法.
其中G关于运算 为“融洽集”的是________(写出所有“融洽集”的序号).
【解析】 ②错,不满足条件(2);④错,不满足条件(1),如a=x2+y2,b=-x2
-y2;⑤错,不满足条件(1),如a=3i,b=4i.
【答案】 ①③
三、解答题
8.已知集合A={-4,2a-1,a2},B={a-5,1-a,9},分别求适合下列条件的a的值.
(1)9∈A∩B;
(2){9}=A∩B.
【解析】 9∈A∩B与{9}=A∩B意义不同,9∈A∩B说明9是A与B的一个公共元素,
但A与B中允许有其他公共元素.
{9}=A∩B,说明A与B的公共元素有且只有一个9,
(1)∵9∈A∩B,∴9∈B且9∈A
∴2a-1=9或a2=9,∴a=5或a=±3.
检验知:a=5或a=-3.
(2)∵{9}=A∩B,∴9∈A∩B,∴a=5或a=-3.检验知:a=-3.
9.设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+(a2-5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围;
(3)若U=R,A∩( UB)=A,求实数a的取值范围.
【解析】 由x2-3x+2=0得x=1或x=2,
故集合A={1,2}.
(1)∵A∩B={2}.
∴2∈B,代入B中的方程,
得a2+4a+3=0 a=-1或a=-3;
当a=-1时,B={x|x2-4=0}={-2,2},满足条件;
当a=-3时,B={x|x2-4x+4=0}={2},满足条件,
综上,a的值为-1或-3.
(2)对于集合B,Δ=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B A,
【答案】 B
从近两年课改区高考试题来看,主要以选择题的形式考查,分值为5分,属容
易题.两集合的交、并、补运算及两集合的包含关系是高考的热点,同时集合常与
方程、不等式相结合,考查方向 、不等式的解法.
从高考试题看,试题由考查单一知识点向两个知识点发展,预测2013年高考仍
将以集合的交、并、补集运算为主要考点,考查学生对基本知识的掌握程度.
【答案】 ①②
【方法指导】 1.集合中的元素的三个性质,特别是无序性和互异性在解题时经
常用到.解题后要进行检验,要重视符号语言与文字语言之间的相互转化.
2.对连续数集间的运算,借助数轴的直观性,进行合理转化;对已知连续数集
间的关系,求其中参数的取值范围时,要注意单独考察等号.
3.对离散的数集间的运算,或抽象集合间的运算,可借助Venn图.这是数形结
合思想的又一体现.
1.(理)(2011年高考山东卷)设集合M={x|x2+x-6<0},N={x|1≤x≤3},则M
∩N= ( )
A.[1,2) B.[1,2]
C.(2,3] D.[2,3]
【解析】 集合M=(-3,2),M∩N=(-3,2)∩[1,3]=[1,2).
【答案】 A(文)
(文) (2011年高考山东卷)设集合M={x|(x+3)(x-2)<0},N={x|1≤x≤3},则
M∩N= ( )
A.[1,2) B.[1,2]
C.(2,3] D.[2,3]
【解析】 集合M=(-3,2),M∩N=(-3,2)∩[1,3]=[1,2).
【答案】 A
2.(2011年高考新课标全国卷,1)已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,
则P的子集共有 ( )
A.2个 B.4个
C.6个 D.8个
【解析】 P=M∩N={1,3},
∴P的子集共有22=4个.
【答案】 B
3.(2011年高考北京卷)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范
围是 ( )
A.(-∞,-1] B.[1,+∞)
C. [-1,1] D.(-∞,-1]∪[1,+∞)
【解析】 因为P∪M=P,所以M P,即a∈P,得a2≤1,解得-1≤a≤1,所以a
的取值范围是[-1,1],故选C.
【答案】 C
4.(2012年山东模拟)设S是整数集Z的非空子集,如果 a,b∈S,有ab∈S,
则称S关于数的乘法是封闭的.若T,V是Z的两个不相交的非空子集,T∪V=
Z, 且 a,b,c∈T,有abc∈T; x,y,z∈V,有xyz∈V,则下列结论恒成立
的是 ( )
A.T,V中至少有一个关于乘法是封闭的
B.T,V中至多有一个关于乘法是封闭的
C.T,V中有且只有一个关于乘法是封闭的
D.T,V中每一个关于乘法都是封闭的
【解析】 不妨设1∈T,则对于 a,b∈T,∵ a,b,c∈T,都有abc∈T,不
妨令c=1,则ab∈T,故T关于乘法是封闭的,故T、V中至少有一个关于乘法是封
闭的;若T为偶数集,V为奇数集,则它们符合题意,且均是关于乘法是封闭的,
从而B、C错误;若T为非负整数集,V为负整数集,显然T、V是Z的两个不相交的
非空子集,T∪V=Z,且 a,b,c∈T,有abc∈T, x,y,z∈V,有xyz∈V,但
是对于 x,y∈V,有xy>0,xy V,D错误.故选A.
【答案】 A
第一节 集合
一、元素与集合
1.集合中元素的三个特性: 、 、 .
2.集合中元素与集合的关系.
元素与集合之间的关系有 和 两种,表示符号为 和 .
3.常见集合的符号表示.
4. 集合的表示法: 、 、 .
确定性
互异性
无序性
属于
不属于
∈
N
N*或N+
Z
Q
R
列举法
描述法
Venn图法
二、集合间的基本关系
定义 记法
集合
间的
基本
关系 相等 集合A与集合B中的所有元素都相同
子集 A中任意一元素均为B中的元素 或
真子集 A中任意一元素均为B中的元素,且B中至少有一个元素A中没有
空集 空集是任何集合的子集
空集是任何 的真子集
关系
表示
或
非空集合
A=B
A B
B A
(B≠ )
三、集合的基本运算
集合的并集 集合的交集 集合的补集
符号表示 若全集为U,则集合A
的补集为
图形表示
意义
A∪B
A∩B
{ x | x ∈ A 或
x∈ B }
且 x∈ B }
{ x | x ∈ A
{ x | x ∈ U 且 x A }
1.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦
恩(Venn)图是 ( )
2.已知集合M={0,1,2},N={x|x=2a,a∈M},则集合M∩N= ( )
A.{0} B.{0,1}
C.{1,2} D.{0,2}
【解析】 ∵M={0,1,2},N={x|x=2a,a∈M},
∴N={0,2,4},∴M∩N={0,2}.
【答案】 D
3.(2011年高考安徽卷,2)集合U={1,2,3,4,5,6},S={1,4,5},T={2,3,4},则
S∩( UT)等于 ( )
A.{1,4,5,6} B.{1,5}
C.{4} D.{1,2,3,4,5}
【解析】 S∩( UT)={1,4,5}∩{1,5,6}={1,5}.
【答案】 B
4.设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B=______.
【解析】 ∵A∩B={2},∴log2(a+3)=2.∴a=1,b=2.
∴A={5,2},B={1,2}.∴A∪B={1,2,5}.
【答案】 {1,2,5}
5.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是_____.
【解析】 借助数轴可知a≤1,如图所示.
【答案】 a≤1
考点一 集合的基本概念
1.掌握集合的概念,关键是把握集合中元素的特性,要特别注意集合中元素的
互异性,一方面利用集合元素的互异性能顺利找到解题的切入点;另一方面,
在解答完毕之时,注意检验集合的元素是否满足互异性以确保答案正确.
2.用描述法表示集合时,首先应清楚集合的类型和元素的性质.如集合{y|y=2x
},{x|y=2x},{(x,y)|y=2x}表示不同的集合.
在数集{2x,x2-x}中,实数x的取值范围是______.
【自主解答】 实数x的取值满足集合元素的互异性,则2x≠x2-x,解得x≠0
且x≠3,
∴实数x的取值范围是{x|x<0或0<x<3或x>3}.
【答案】 {x|x<0或0<x<3或x>3}
【答案】 C
考点二 集合间的基本关系
1.子集与真子集的区别与联系:集合A的真子集一定是其子集,而集合A的子集
不一定是其真子集;若集合A有n个元素,则其子集个数为2n,真子集个数为
2n-1.
2.判断集合与集合的关系,基本方法是归纳为判断元素与集合的关系.对于用
描述法表示的集合,要紧紧抓住代表元素及它的属性,可将元素列举出来直
观发现或通过元素特征,求同存异,定性分析.应做到意义化(分清集合的种
类,数集、点集、图形、定义域、值域、方程或不等式的解或解集等)、具体
化(具体求出相关的集合并化简)、直观化(借助数轴、Venn图、函数图象等,
即数形结合的思想).
已知集合A={x|x2-3x+2≤0},B={x|x2-(a+1)x+a≤0}.
(1)若A?B,求a的取值范围;
(2)若B A,求a的取值范围;
(3)若A=B,求a的取值范围.
【思路点拨】 解决本题的关键是将B集合化简,即因式分解,再根据A,B间
的关系求解.
【自主解答】 由x2-3x+2≤0,即(x-1)(x-2)≤0,
得1≤x≤2,故A={x|1≤x≤2},
而集合B={x|(x-1)(x-a)≤0},
则(1)若A是B的真子集,即A?B,
则此时B={x|1≤x≤a},故a>2.
(2)若B是A的子集,即B A,由数轴可知1≤a≤2.
(3)若A=B,则必有a=2.
2.已知集合A={x|x2-3x-10≤0},
(1)若B A,B={x|m+1≤x≤2m-1},求实数m的取值范围;
(2)若A B,B={x|m-6≤x≤2m-1},求实数m的取值范围;
(3)若A=B,B={x|m-5≤x≤2m-1},求实数m的值.
【自主解答】 (1)由A={x|x2-3x-10≤0},得
A={x|-2≤x≤5},∵B A,
∴①若B= ,则m+1>2m-1,即m<2,此时满足B A.
②若B≠ ,
考点三 集合的基本运算
在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化.一般
地,集合元素离散时用Venn图表示;集合元素连续时用数轴表示,用数轴表示时
注意端点值的取舍.
【思路点拨】 利用集合A,B的关系,借助数轴,列出关于a的不等式组求解.
(1分)
(5分)
(8分)
3.已知集合A={x|x2-6x+8<0},B={x|(x-a)(x-3a)<0}.
(1)若A B,求a的取值范围;
(2)若A∩B= ,求a的取值范围;
(3)若A∩B={x|3<x<4},求a的取值范围.
一、选择题
1.已知集合M={x |-3<x≤5},N={ x | x<-5或 x>5},则M∪N=( )
A.{x | x<-5 或 x>-3} B.{x|-5<x<5}
C.{x|-3<x<5} D.{x | x<-3或 x>5}
【解析】
由题意画出图形.可知,M∪N={x|x<-5或x>-3}.
【答案】 A
【答案】 B
3.(2011年高考广东卷,2)已知集合A={(x,y)|x,y为实数,且x2+y2=1},B=
{(x,y)|x,y为实数,且y=x},则A∩B的元素个数为 ( )
A.3 B.2
C.1 D.0
【答案】 B
4.设全集U是实数集R,M={x|x2>4},N={x|x≥3或x<1}都是U的子集,则图中
阴影部分所表示的集合是 ( )
A.{x|-2≤x<1}
B.{x|-2≤x≤2}
C.{x|1<x≤2}
D.{x|x<2}
【解析】 图中阴影部分表示N∩( UM),
∵M={|x2>4}={x|x>2或x<-2}
∴ UM={x|-2≤x≤2},
∴N∩( UM)={-2≤x<1}.
【答案】 A
【答案】 A
二、填空题
6.(2012年天津模拟)已知集合A={x∈R||x-1|<2},Z为整数集,则集合A∩Z
中所有元素的和等于________.
【解析】 A={x|-1<x<3},A∩Z={0,1,2},A∩Z中所有元素之和等于3.
【答案】 3
7.非空集合G关于运算 满足:(1)对任意a、b∈G,都有a b∈G;(2)存在e∈G,
使得对一切a∈G,都有a e=e a=a,则称G关于运算 为“融洽集”.现给
出下列集合和运算:
①G={非负整数}, 为整数的加法.
②G={偶数}, 为整数的乘法.
③G={平面向量}, 为平面向量的加法.
④G={二次三项式}, 为多项式的加法.
⑤G={虚数}, 为复数的乘法.
其中G关于运算 为“融洽集”的是________(写出所有“融洽集”的序号).
【解析】 ②错,不满足条件(2);④错,不满足条件(1),如a=x2+y2,b=-x2
-y2;⑤错,不满足条件(1),如a=3i,b=4i.
【答案】 ①③
三、解答题
8.已知集合A={-4,2a-1,a2},B={a-5,1-a,9},分别求适合下列条件的a的值.
(1)9∈A∩B;
(2){9}=A∩B.
【解析】 9∈A∩B与{9}=A∩B意义不同,9∈A∩B说明9是A与B的一个公共元素,
但A与B中允许有其他公共元素.
{9}=A∩B,说明A与B的公共元素有且只有一个9,
(1)∵9∈A∩B,∴9∈B且9∈A
∴2a-1=9或a2=9,∴a=5或a=±3.
检验知:a=5或a=-3.
(2)∵{9}=A∩B,∴9∈A∩B,∴a=5或a=-3.检验知:a=-3.
9.设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+(a2-5)=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围;
(3)若U=R,A∩( UB)=A,求实数a的取值范围.
【解析】 由x2-3x+2=0得x=1或x=2,
故集合A={1,2}.
(1)∵A∩B={2}.
∴2∈B,代入B中的方程,
得a2+4a+3=0 a=-1或a=-3;
当a=-1时,B={x|x2-4=0}={-2,2},满足条件;
当a=-3时,B={x|x2-4x+4=0}={2},满足条件,
综上,a的值为-1或-3.
(2)对于集合B,Δ=4(a+1)2-4(a2-5)=8(a+3).
∵A∪B=A,∴B A,
【答案】 B
从近两年课改区高考试题来看,主要以选择题的形式考查,分值为5分,属容
易题.两集合的交、并、补运算及两集合的包含关系是高考的热点,同时集合常与
方程、不等式相结合,考查方向 、不等式的解法.
从高考试题看,试题由考查单一知识点向两个知识点发展,预测2013年高考仍
将以集合的交、并、补集运算为主要考点,考查学生对基本知识的掌握程度.
【答案】 ①②
【方法指导】 1.集合中的元素的三个性质,特别是无序性和互异性在解题时经
常用到.解题后要进行检验,要重视符号语言与文字语言之间的相互转化.
2.对连续数集间的运算,借助数轴的直观性,进行合理转化;对已知连续数集
间的关系,求其中参数的取值范围时,要注意单独考察等号.
3.对离散的数集间的运算,或抽象集合间的运算,可借助Venn图.这是数形结
合思想的又一体现.
1.(理)(2011年高考山东卷)设集合M={x|x2+x-6<0},N={x|1≤x≤3},则M
∩N= ( )
A.[1,2) B.[1,2]
C.(2,3] D.[2,3]
【解析】 集合M=(-3,2),M∩N=(-3,2)∩[1,3]=[1,2).
【答案】 A(文)
(文) (2011年高考山东卷)设集合M={x|(x+3)(x-2)<0},N={x|1≤x≤3},则
M∩N= ( )
A.[1,2) B.[1,2]
C.(2,3] D.[2,3]
【解析】 集合M=(-3,2),M∩N=(-3,2)∩[1,3]=[1,2).
【答案】 A
2.(2011年高考新课标全国卷,1)已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,
则P的子集共有 ( )
A.2个 B.4个
C.6个 D.8个
【解析】 P=M∩N={1,3},
∴P的子集共有22=4个.
【答案】 B
3.(2011年高考北京卷)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范
围是 ( )
A.(-∞,-1] B.[1,+∞)
C. [-1,1] D.(-∞,-1]∪[1,+∞)
【解析】 因为P∪M=P,所以M P,即a∈P,得a2≤1,解得-1≤a≤1,所以a
的取值范围是[-1,1],故选C.
【答案】 C
4.(2012年山东模拟)设S是整数集Z的非空子集,如果 a,b∈S,有ab∈S,
则称S关于数的乘法是封闭的.若T,V是Z的两个不相交的非空子集,T∪V=
Z, 且 a,b,c∈T,有abc∈T; x,y,z∈V,有xyz∈V,则下列结论恒成立
的是 ( )
A.T,V中至少有一个关于乘法是封闭的
B.T,V中至多有一个关于乘法是封闭的
C.T,V中有且只有一个关于乘法是封闭的
D.T,V中每一个关于乘法都是封闭的
【解析】 不妨设1∈T,则对于 a,b∈T,∵ a,b,c∈T,都有abc∈T,不
妨令c=1,则ab∈T,故T关于乘法是封闭的,故T、V中至少有一个关于乘法是封
闭的;若T为偶数集,V为奇数集,则它们符合题意,且均是关于乘法是封闭的,
从而B、C错误;若T为非负整数集,V为负整数集,显然T、V是Z的两个不相交的
非空子集,T∪V=Z,且 a,b,c∈T,有abc∈T, x,y,z∈V,有xyz∈V,但
是对于 x,y∈V,有xy>0,xy V,D错误.故选A.
【答案】 A
同课章节目录
