2012江苏高考数学考前每天必看(7天)
图片预览
文档简介
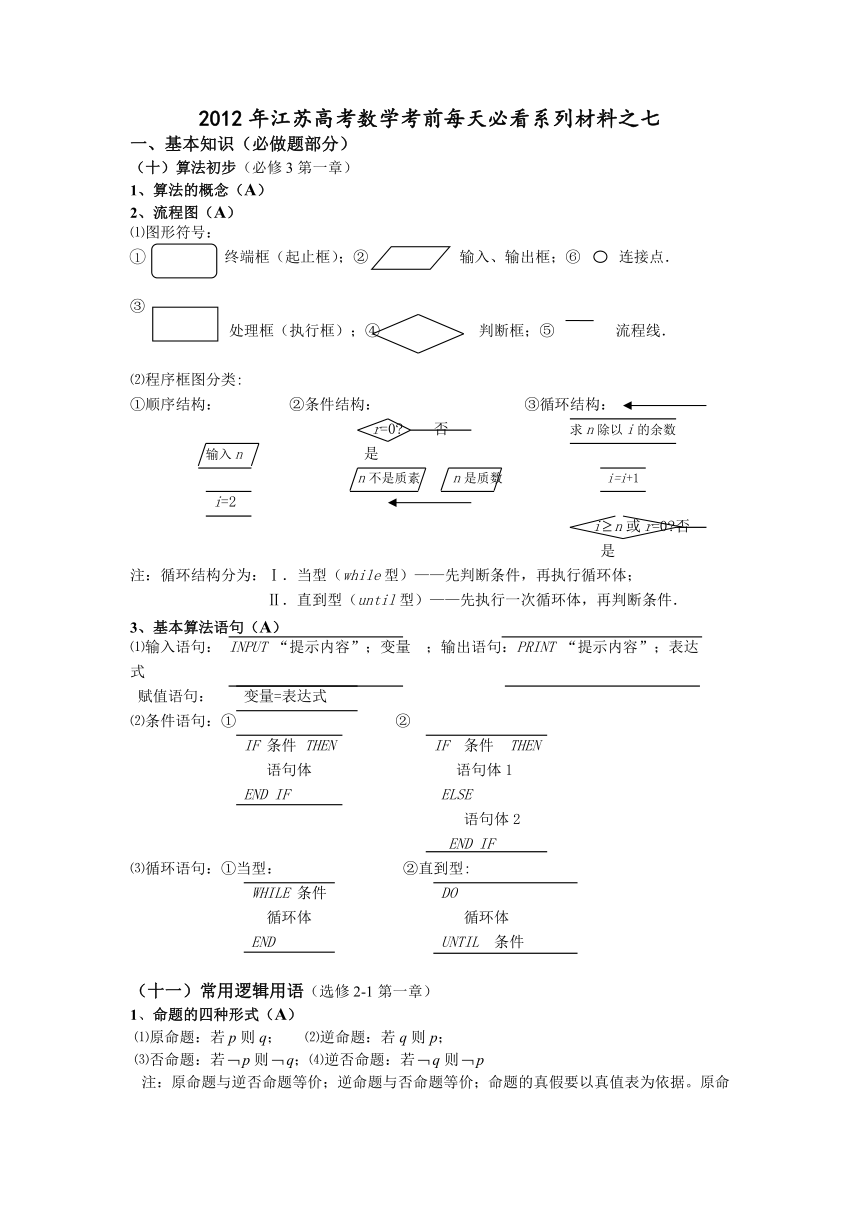
2012年江苏高考数学考前每天必看系列材料之七
一、基本知识(必做题部分)
(十)算法初步(必修3第一章)
1、算法的概念(A)
2、流程图(A)
⑴图形符号:
终端框(起止框);② 输入、输出框;⑥ 连接点.
③
处理框(执行框);④ 判断框;⑤ 流程线.
⑵程序框图分类:
①顺序结构: ②条件结构: ③循环结构:
r=0 否 求n除以i的余数
输入n 是
n不是质素 n是质数 i=i+1
i=2
in或r=0 否
是
注:循环结构分为:Ⅰ.当型(while型)——先判断条件,再执行循环体;
Ⅱ.直到型(until型)——先执行一次循环体,再判断条件.
3、基本算法语句(A)
⑴输入语句: INPUT “提示内容”;变量 ;输出语句:PRINT “提示内容”;表达式
赋值语句: 变量=表达式
⑵条件语句:① ②
IF 条件 THEN IF 条件 THEN
语句体 语句体1
END IF ELSE
语句体2
END IF
⑶循环语句:①当型: ②直到型:
WHILE 条件 DO
循环体 循环体
END UNTIL 条件
(十一)常用逻辑用语(选修2-1第一章)
1、命题的四种形式(A)
⑴原命题:若p则q; ⑵逆命题:若q则p;
⑶否命题:若p则q;⑷逆否命题:若q则p
注:原命题与逆否命题等价;逆命题与否命题等价;命题的真假要以真值表为依据。原命题与其逆否命题是等价命题,逆命题与其否命题是等价命题,一真俱真,一假俱假,当一个命题的真假不易判断时,可考虑判断其等价命题的真假.
2、充分条件,必要条件,充分必要条件(B)
(1)定义法;
(2)利用集合间的包含关系判断,若,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
(3)等价法:即利用等价关系判断,对于条件或结论是不等关系(或否定式)的命题,一般运用等价法.
p Q pq pq p
真 真 真 真 假
真 假 假 真 假
假 真 假 真 真
假 假 假 假 真
3、简单的逻辑逻辑联结词(A)
⑴且(and) :命题形式 pq;
⑵或(or):命题形式 pq;
⑶非(not):命题形式p .
4、全称量词与存在量词(A)
⑴全称量词-------“所有的”、“任意一个”等,用表示;
全称命题p:; 全称命题p的否定p:.
⑵存在量词--------“存在一个”、“至少有一个”等,用表示;
存在命题p:; 存在命题p的否定p:.
(十二)推理证明(选修2-2 第二章)
1、合情推理与演绎推理(B)
归纳推理和类比推理都是根据已有事实,经过观察、分析、比较、联想,在进行归纳、类比,然后提出猜想的推理,我们把它们称为合情推理.
①归纳推理:由某类食物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者有个别事实概括出一般结论的推理,称为归纳推理,简称归纳.
注:归纳推理是由部分到整体,由个别到一般的推理.
②类比推理:由两类对象具有类似和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,称为类比推理,简称类比.
注:类比推理是特殊到特殊的推理.
③演绎推理:从一般的原理出发,推出某个特殊情况下的结论,这种推理叫演绎推理.
注:演绎推理是由一般到特殊的推理.
“三段论”是演绎推理的一般模式,包括:⑴大前提---------已知的一般结论;⑵小前提---------所研究的特殊情况;⑶结 论---------根据一般原理,对特殊情况得出的判断.
2、分析法与综合法(A)
⑴综合法:一般地,利用已知条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。综合法又叫顺推法或由因导果法.
⑵分析法:一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等),这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法.
3、反证法(A)一般地,假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这种证明方法叫反证法.
二、思想方法
(七)分析法、综合法
(1)分析法是从所求证的结果出发,逐步推出能使它成立的条件,直至已知的事实为止;分析法是一种“执果索因”的直接证法.
(2)综合法是从已经证明的结论、公式出发,逐步推出所要求证的结论.综合法是一种“由因导果”,叙述流畅的直接证法.
(3)分析法、 综合法是证明数学问题的两大最基本的方法。分析法“执果索因”的分析方法,思路清晰,容易找到解题路子,但书写格式要求较高,不容易叙述清楚,所以分析法、综合法常常交替使用.分析法、 综合法应用很广,几乎所有题都可以用这两个方法来解.
(八)反证法
反证法是数学证明的一种重要方法,因为命题p与它的否定非p的真假相反,所以要证一个命题为真,只要证它的否定为假即可.这种从证明矛盾命题(即命题的否定)为假进而证明命题为真的证明方法叫做反证法.
㈠ 反证法证明的一般步骤是:
(1)反设:假设命题的结论不成立,即假设结论的反面成立;
(2)归谬:从命题的条件和所作的结论出发,经过正确的推理论证,得出矛盾的结果;
(3)结论:有矛盾判定假设不正确,从而肯定的结论正确.
㈡ 反证法的适用范围:(1)已知条件很少或由已知条件能推得的结论很少时的命题;
(2)结论的反面是比原结论更具体、更简单的命题,特别是结论是否定形式(“不是”、“不可能”、“不可得”)等的命题;(3)涉及各种无限结论的命题;(4)以“最多(少)、若干个”为结论的命题;(5)存在性命题;(6)唯一性命题;(7)某些定理的逆定理;(8)一般关系不明确或难于直接证明的不等式等.
㈢ 反证法的逻辑依据是“矛盾律”和“排中律” .
一、基本知识(必做题部分)
(十)算法初步(必修3第一章)
1、算法的概念(A)
2、流程图(A)
⑴图形符号:
终端框(起止框);② 输入、输出框;⑥ 连接点.
③
处理框(执行框);④ 判断框;⑤ 流程线.
⑵程序框图分类:
①顺序结构: ②条件结构: ③循环结构:
r=0 否 求n除以i的余数
输入n 是
n不是质素 n是质数 i=i+1
i=2
in或r=0 否
是
注:循环结构分为:Ⅰ.当型(while型)——先判断条件,再执行循环体;
Ⅱ.直到型(until型)——先执行一次循环体,再判断条件.
3、基本算法语句(A)
⑴输入语句: INPUT “提示内容”;变量 ;输出语句:PRINT “提示内容”;表达式
赋值语句: 变量=表达式
⑵条件语句:① ②
IF 条件 THEN IF 条件 THEN
语句体 语句体1
END IF ELSE
语句体2
END IF
⑶循环语句:①当型: ②直到型:
WHILE 条件 DO
循环体 循环体
END UNTIL 条件
(十一)常用逻辑用语(选修2-1第一章)
1、命题的四种形式(A)
⑴原命题:若p则q; ⑵逆命题:若q则p;
⑶否命题:若p则q;⑷逆否命题:若q则p
注:原命题与逆否命题等价;逆命题与否命题等价;命题的真假要以真值表为依据。原命题与其逆否命题是等价命题,逆命题与其否命题是等价命题,一真俱真,一假俱假,当一个命题的真假不易判断时,可考虑判断其等价命题的真假.
2、充分条件,必要条件,充分必要条件(B)
(1)定义法;
(2)利用集合间的包含关系判断,若,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
(3)等价法:即利用等价关系判断,对于条件或结论是不等关系(或否定式)的命题,一般运用等价法.
p Q pq pq p
真 真 真 真 假
真 假 假 真 假
假 真 假 真 真
假 假 假 假 真
3、简单的逻辑逻辑联结词(A)
⑴且(and) :命题形式 pq;
⑵或(or):命题形式 pq;
⑶非(not):命题形式p .
4、全称量词与存在量词(A)
⑴全称量词-------“所有的”、“任意一个”等,用表示;
全称命题p:; 全称命题p的否定p:.
⑵存在量词--------“存在一个”、“至少有一个”等,用表示;
存在命题p:; 存在命题p的否定p:.
(十二)推理证明(选修2-2 第二章)
1、合情推理与演绎推理(B)
归纳推理和类比推理都是根据已有事实,经过观察、分析、比较、联想,在进行归纳、类比,然后提出猜想的推理,我们把它们称为合情推理.
①归纳推理:由某类食物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者有个别事实概括出一般结论的推理,称为归纳推理,简称归纳.
注:归纳推理是由部分到整体,由个别到一般的推理.
②类比推理:由两类对象具有类似和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,称为类比推理,简称类比.
注:类比推理是特殊到特殊的推理.
③演绎推理:从一般的原理出发,推出某个特殊情况下的结论,这种推理叫演绎推理.
注:演绎推理是由一般到特殊的推理.
“三段论”是演绎推理的一般模式,包括:⑴大前提---------已知的一般结论;⑵小前提---------所研究的特殊情况;⑶结 论---------根据一般原理,对特殊情况得出的判断.
2、分析法与综合法(A)
⑴综合法:一般地,利用已知条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。综合法又叫顺推法或由因导果法.
⑵分析法:一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等),这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法.
3、反证法(A)一般地,假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这种证明方法叫反证法.
二、思想方法
(七)分析法、综合法
(1)分析法是从所求证的结果出发,逐步推出能使它成立的条件,直至已知的事实为止;分析法是一种“执果索因”的直接证法.
(2)综合法是从已经证明的结论、公式出发,逐步推出所要求证的结论.综合法是一种“由因导果”,叙述流畅的直接证法.
(3)分析法、 综合法是证明数学问题的两大最基本的方法。分析法“执果索因”的分析方法,思路清晰,容易找到解题路子,但书写格式要求较高,不容易叙述清楚,所以分析法、综合法常常交替使用.分析法、 综合法应用很广,几乎所有题都可以用这两个方法来解.
(八)反证法
反证法是数学证明的一种重要方法,因为命题p与它的否定非p的真假相反,所以要证一个命题为真,只要证它的否定为假即可.这种从证明矛盾命题(即命题的否定)为假进而证明命题为真的证明方法叫做反证法.
㈠ 反证法证明的一般步骤是:
(1)反设:假设命题的结论不成立,即假设结论的反面成立;
(2)归谬:从命题的条件和所作的结论出发,经过正确的推理论证,得出矛盾的结果;
(3)结论:有矛盾判定假设不正确,从而肯定的结论正确.
㈡ 反证法的适用范围:(1)已知条件很少或由已知条件能推得的结论很少时的命题;
(2)结论的反面是比原结论更具体、更简单的命题,特别是结论是否定形式(“不是”、“不可能”、“不可得”)等的命题;(3)涉及各种无限结论的命题;(4)以“最多(少)、若干个”为结论的命题;(5)存在性命题;(6)唯一性命题;(7)某些定理的逆定理;(8)一般关系不明确或难于直接证明的不等式等.
㈢ 反证法的逻辑依据是“矛盾律”和“排中律” .
同课章节目录
