2021—2022学年人教版数学八年级上册11.1 .1 三角形的边课件(18张)
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册11.1 .1 三角形的边课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 19:14:34 | ||
图片预览



文档简介
(共18张PPT)
11.1.1
三角形的边
第十一章
三角形
情境引入
学习目标
1.认识三角形并会用符号语言表示三角形,了解三角
形的分类.
2.掌握三角形的三边关系.
3.运用三角形三边关系解决有关的问题.
情景引入
一、自主学习
A
B
C
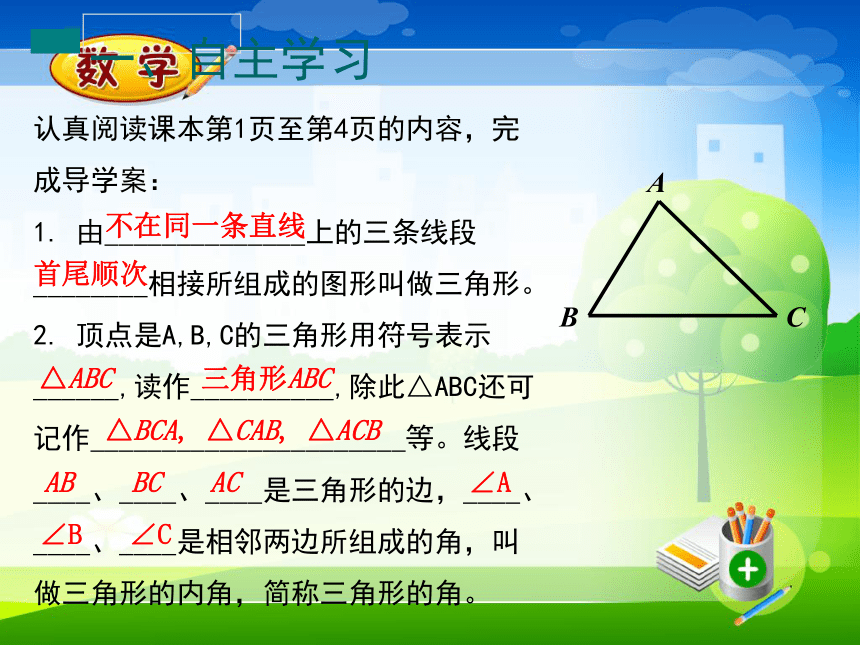
认真阅读课本第1页至第4页的内容,完成导学案:
1.
由______________上的三条线段________相接所组成的图形叫做三角形。
2.
顶点是A,B,C的三角形用符号表示______,读作__________,除此△ABC还可记作______________________等。线段____、____、____是三角形的边,____、____、____是相邻两边所组成的角,叫做三角形的内角,简称三角形的角。
不在同一条直线
首尾顺次
△ABC
三角形ABC
△BCA,
△CAB,
△ACB
AB
BC
AC
∠A
∠B
∠C
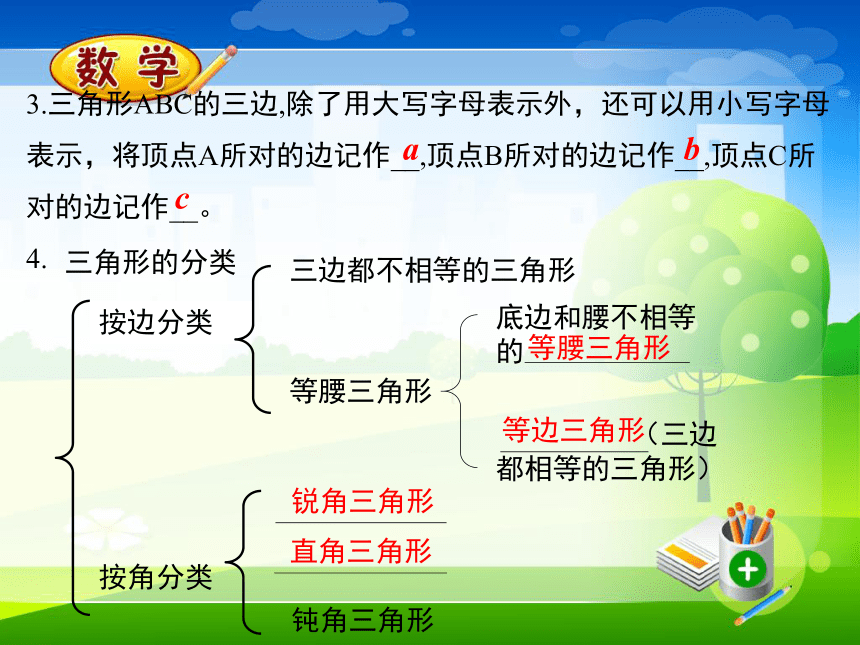
3.三角形ABC的三边,除了用大写字母表示外,还可以用小写字母表示,将顶点A所对的边记作__,顶点B所对的边记作__,顶点C所对的边记作__。
4.
a
b
c
三角形的分类
按边分类
按角分类
三边都不相等的三角形
等腰三角形
底边和腰不相等
的
(三边都相等的三角形)
钝角三角形
锐角三角形
直角三角形
等腰三角形
等边三角形
二、
合作互助
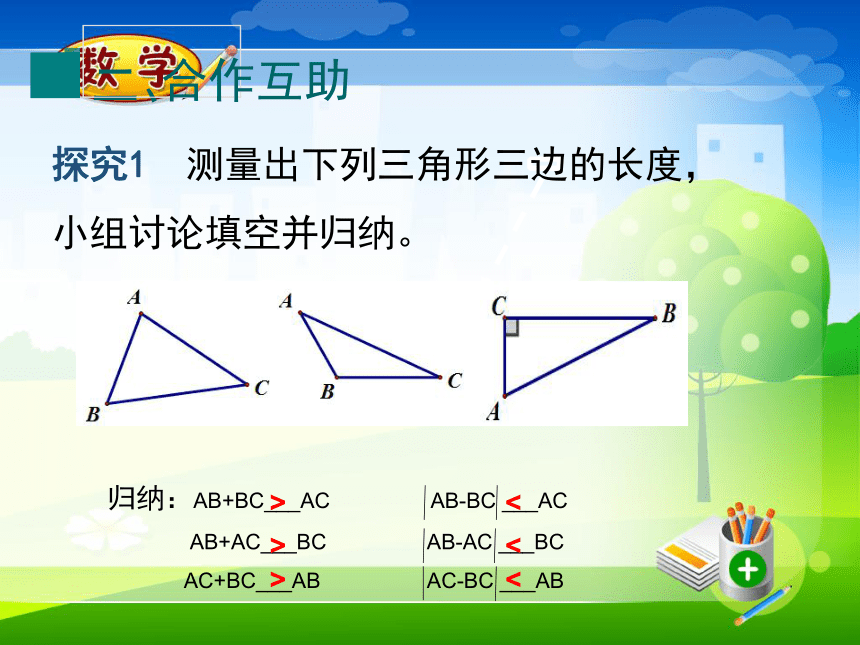
探究1
测量出下列三角形三边的长度,小组讨论填空并归纳。
归纳:AB+BC___AC
AB-BC
___AC
AB+AC___BC
AB-AC
___BC
AC+BC___AB
AC-BC
___AB
>
>
>
<
<
<
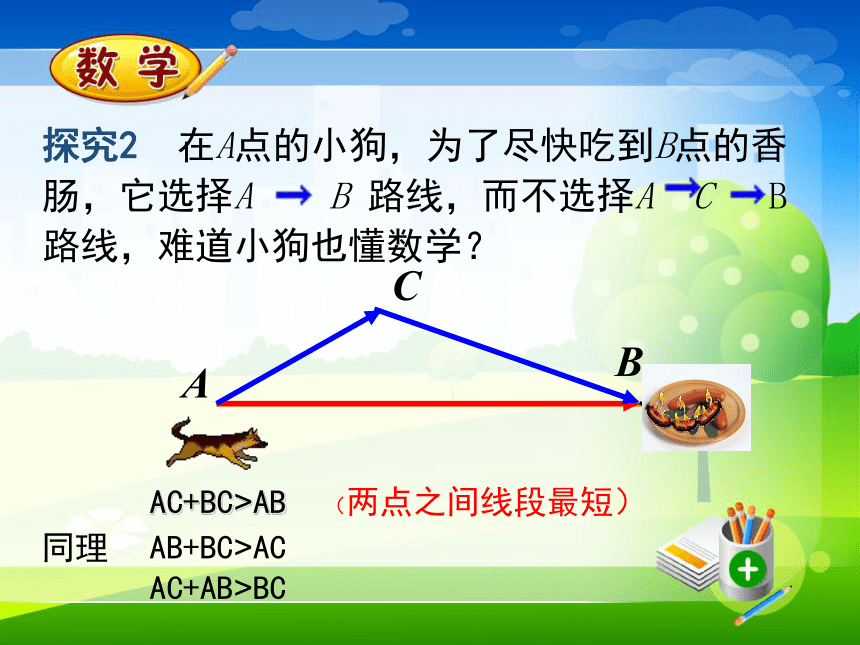
探究2
在A点的小狗,为了尽快吃到B点的香肠,它选择A
B
路线,而不选择A
C
B路线,难道小狗也懂数学?
C
B
A
AC+BC>AB
同理
AB+BC>AC
AC+AB>BC
(两点之间线段最短)
那又怎样证明三角形任意两边之差小于第三边呢?
归纳总结
三角形任意两边的和大于第三边.
三角形任意两边的差小于第三边.
移项得
即
BC>
AB-AC
BC>AB-AC
BC>AC-AB
例1
有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:当取长度为2cm的木棒时,
∵2+5=7<8,出现了两边之和小于第三边的情况
∴它们不能摆成三角形.
当取长度为13cm的木棒时,
∵5+8=13,出现了两边之和等于第三边的情况
∴它们也不能摆成三角形.
归纳
三、重点强化
例2
一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解:∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.
A
例3
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成一边长是4cm的等腰三角形吗?为什么
?
解:(1)设底边长为xcm,则腰长为2xcm,
x+2x+2x=18.
解得
x=3.6.
所以三边长分别为3.6cm、7.2cm、7.2cm.
(2)因为长为4cm的边可能是腰,也可能是底边,
所以需要分情况讨论.
①若底边长为4cm,设腰长为xcm,则有
4+2x=18.
解得
x=7.
②若腰长为4cm,设底边长为xcm,则有
2×4+x=18.
解得
x=10.
因为4+4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边长是4cm的等腰三角形.
分类讨论的思想方法
1.下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
5,6,10
(
)
(3)
3,5,8
(
)
不能
能
不能
四、展示效果
3.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成________个三角形.
3
18cm或21cm
4.若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
解:设第三边长为x,根据三角形的三边关系,可得,
7-2<x<7+2,即5<x<9,
又x为奇数,则第三边的长为7.
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
不重不漏
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|(x为第三边)
应用
五、总结提升
本节课你学到了什么?
1.如图,D是△ABC
的边AC上一点,AD=BD,试判断AC
与BC
的大小.
解:在△BDC
中,
有
BD+DC
>BC(三角形的
任意两边之和大于第三边).
又因为
AD
=
BD,
则BD+DC
=
AD+DC
=
AC,
所以
AC
>BC.
2.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
11.1.1
三角形的边
第十一章
三角形
情境引入
学习目标
1.认识三角形并会用符号语言表示三角形,了解三角
形的分类.
2.掌握三角形的三边关系.
3.运用三角形三边关系解决有关的问题.
情景引入
一、自主学习
A
B
C
认真阅读课本第1页至第4页的内容,完成导学案:
1.
由______________上的三条线段________相接所组成的图形叫做三角形。
2.
顶点是A,B,C的三角形用符号表示______,读作__________,除此△ABC还可记作______________________等。线段____、____、____是三角形的边,____、____、____是相邻两边所组成的角,叫做三角形的内角,简称三角形的角。
不在同一条直线
首尾顺次
△ABC
三角形ABC
△BCA,
△CAB,
△ACB
AB
BC
AC
∠A
∠B
∠C
3.三角形ABC的三边,除了用大写字母表示外,还可以用小写字母表示,将顶点A所对的边记作__,顶点B所对的边记作__,顶点C所对的边记作__。
4.
a
b
c
三角形的分类
按边分类
按角分类
三边都不相等的三角形
等腰三角形
底边和腰不相等
的
(三边都相等的三角形)
钝角三角形
锐角三角形
直角三角形
等腰三角形
等边三角形
二、
合作互助
探究1
测量出下列三角形三边的长度,小组讨论填空并归纳。
归纳:AB+BC___AC
AB-BC
___AC
AB+AC___BC
AB-AC
___BC
AC+BC___AB
AC-BC
___AB
>
>
>
<
<
<
探究2
在A点的小狗,为了尽快吃到B点的香肠,它选择A
B
路线,而不选择A
C
B路线,难道小狗也懂数学?
C
B
A
AC+BC>AB
同理
AB+BC>AC
AC+AB>BC
(两点之间线段最短)
那又怎样证明三角形任意两边之差小于第三边呢?
归纳总结
三角形任意两边的和大于第三边.
三角形任意两边的差小于第三边.
移项得
即
BC>
AB-AC
BC>AB-AC
BC>AC-AB
例1
有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:当取长度为2cm的木棒时,
∵2+5=7<8,出现了两边之和小于第三边的情况
∴它们不能摆成三角形.
当取长度为13cm的木棒时,
∵5+8=13,出现了两边之和等于第三边的情况
∴它们也不能摆成三角形.
归纳
三、重点强化
例2
一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解:∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.
A
例3
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成一边长是4cm的等腰三角形吗?为什么
?
解:(1)设底边长为xcm,则腰长为2xcm,
x+2x+2x=18.
解得
x=3.6.
所以三边长分别为3.6cm、7.2cm、7.2cm.
(2)因为长为4cm的边可能是腰,也可能是底边,
所以需要分情况讨论.
①若底边长为4cm,设腰长为xcm,则有
4+2x=18.
解得
x=7.
②若腰长为4cm,设底边长为xcm,则有
2×4+x=18.
解得
x=10.
因为4+4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边长是4cm的等腰三角形.
分类讨论的思想方法
1.下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
5,6,10
(
)
(3)
3,5,8
(
)
不能
能
不能
四、展示效果
3.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成________个三角形.
3
18cm或21cm
4.若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
解:设第三边长为x,根据三角形的三边关系,可得,
7-2<x<7+2,即5<x<9,
又x为奇数,则第三边的长为7.
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
不重不漏
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|
应用
五、总结提升
本节课你学到了什么?
1.如图,D是△ABC
的边AC上一点,AD=BD,试判断AC
与BC
的大小.
解:在△BDC
中,
有
BD+DC
>BC(三角形的
任意两边之和大于第三边).
又因为
AD
=
BD,
则BD+DC
=
AD+DC
=
AC,
所以
AC
>BC.
2.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
