2.6受迫振动 共振 课件—2021-2022学年高二上学期物理人教版(2019)选择性必修第一册(29张PPT)
文档属性
| 名称 | 2.6受迫振动 共振 课件—2021-2022学年高二上学期物理人教版(2019)选择性必修第一册(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-12 16:38:32 | ||
图片预览







文档简介
2.6受迫振动 共振
学习重点:受迫振动时其频率跟驱动力频率的关系,共振。
学习难点:受迫振动时其频率跟驱动力频率的关系。
思考:你知道为什么大钟会无缘无故地鸣响吗?
东汉以后三国纷争年代,有一天,魏都洛阳宫殿前面的一口大钟,突然无缘无故地鸣响起来,满朝文武议论纷纷,有的以为是不祥之兆,也有人乘机献媚,把它说成是祥瑞。
一、振动中的能量损失
1. 固有振动
思考:让单摆、弹簧振子自由振动,忽略空气阻力,则单摆,弹簧振子做什么运动?
单摆,弹簧振子做简谐运动,周期或频率与振幅无关,仅由系统自身的性质决定。
(1)固有振动:简谐运动的周期或频率与振幅无关,仅由系统自身的性质决定,我们把这种振动称为固有振动。?
(2)固有频率:物体固有振动时的频率仅有系统自身的性质决定,称固有频率。
2.阻尼振动
(2)实际的振动一定是阻尼振动。
(1)阻尼振动:振幅随时间逐渐减小的振动称为阻尼振动。
摇曳的树叶会停下来,摆动的秋千也会停止运动。
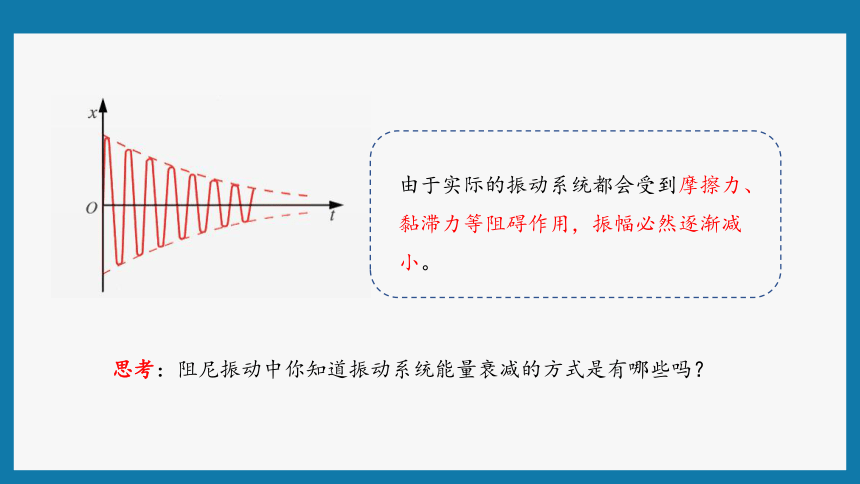
思考:阻尼振动中你知道振动系统能量衰减的方式是有哪些吗?
由于实际的振动系统都会受到摩擦力、黏滞力等阻碍作用,振幅必然逐渐减小。
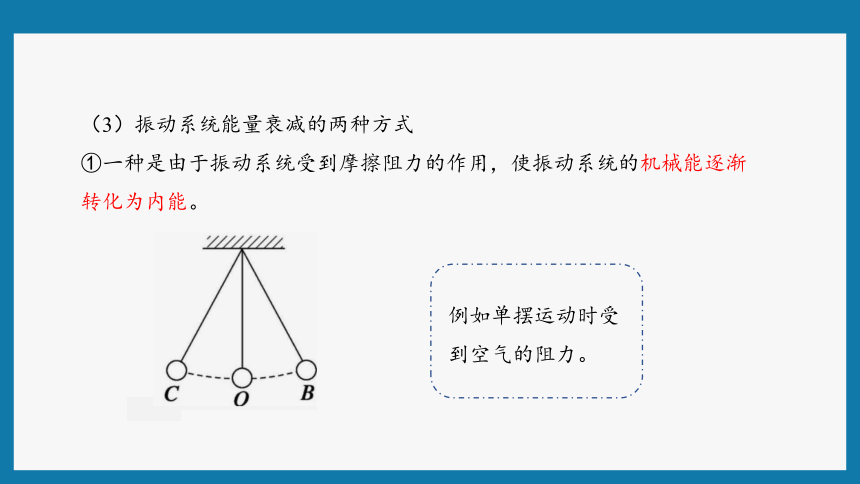
(3)振动系统能量衰减的两种方式
①一种是由于振动系统受到摩擦阻力的作用,使振动系统的机械能逐渐转化为内能。
例如单摆运动时受到空气的阻力。
②另一种是由于振动系统引起邻近介质中各质点的振动,使能量向四周
辐射出去,从而自身机械能减少。
例如音叉发声时,一部分机械能随声波辐射到周围空间,导致音叉振幅减小。
特别提醒!
(1)振动系统受到的阻尼越大,振幅减小得越快,阻尼过大时,系统将不能发生振动。
(2)阻尼振动的振幅是逐渐减小的,但是它的频率是不发生变化的,频率与振幅是无关的。
思考:阻尼振动最终要停下来,那么怎样才能产生持续的振动呢?
例1.如图所示是某单摆做阻尼振动的振动图线,下列说法正确的是( )
A.振动过程中周期变小
B.摆球P时刻的机械能大于N时刻的
机械能
C.摆球P时刻的动能等于N时刻的动能
D.小球在P时刻和N时刻,受到绳子拉
力的大小相等
B
【答案】B
【详解】
A.阻尼振动的周期不变,振幅减小,故A错误;
BC.由于阻力影响,单摆要克服阻力做功,在运动过程中机械能一直逐渐减小,故P时刻的机械能大于N时刻的机械能,而两点重力势能相等,则P时刻的动能大于N时刻的动能,故B正确,C错误;
D.因为PN两时刻位置关于平衡位置对称,但是速度不等,则两时刻受到绳子的拉力大小不相等,故D错误;
故选B。
变式训练:如图所示是单摆做阻尼振动的位移—时间图线,下列说法中正确的是( )
A.摆球在P与N时刻的势能相等
B.摆球在P与N时刻的动能相等
C.摆球在P与N时刻的机械能相等
D.摆球在P时刻的机械能小于在N时刻的机械能
A
技法点拨:
(1)摆球的势能大小由其位移和摆球质量共同决定,由图可知P、N两时刻位移大小相同,则可判断出摆球的势能大小。
(2)机械能E等于动能Ek和势能Ep之和, 阻尼振动中,由于系统机械能在减少E减小, P、N两时刻势能相同,则P时刻动能大于N时刻动能。
产生持续的振动最简单的办法是使周期性的外力作用于振动系统,外力对系统做功,补偿系统的能量损耗,使系统的振动维持下去。
1.驱动力
对振动系统施加的周期性的外力,这种周期性的外力叫作驱动力。
2.受迫振动
系统在驱动力作用下的振动,叫作受迫振动。
机器运转时底座发生的振动、扬声器纸盆的振动,都是受迫振动。
二、受迫振动
实验:研究受迫振动的频率
如图 ,架子上面的电动机向下面的两组弹簧—钩码系统施加周期性的驱动力,使钩码做受迫振动。
改变电动机的转速可以调整驱动力的频率。
思考:物体做受迫振动时,振动稳定后的频率与什么有关?受迫振动物体的频率由什么决定?
(1)接通电源,使钩码做受迫振动,观察记录驱动力的频率和钩码振动的频率。
(2)改变驱动力的频率,再做记录。
研究受迫振动的频率视频
实验结论:
(1)物体做受迫振动达到稳定后,物体振动的频率等于驱动力的频率,与物体的固有频率无关。
(2)驱动力的频率与系统的固有频率相差越少,振幅越大,相差越多,振幅越小。
3.共振现象及其应用
做一做:如图,铁架横梁上挂着几个摆长不同的摆。
其中,A 与 D、G 的摆长相同,D 的摆球质量大于其他摆球。使 D 摆偏离平衡位置后释放,D 摆在振动中通过横梁对其他几个摆施加周期性的驱动力。在振动稳定后比较各球的振幅。
A
D
G
C
E
小球共振实验视频
(1)实验现象:通过观察会发现,固有频率与D摆相同的A摆、G摆振幅最大,固有频率与D摆相差较多的C摆、E摆振幅最小。
(2)实验结论
物体在做受迫振动时,驱动力的频率与物体的固有频率相差越小,受迫振动的振幅越大;当驱动力的频率与物体的固有频率相等时,受迫振动的振幅达到最大。
4.共振
(1)驱动力的频率接近物体的固有频率时,受迫振动的振幅增大,这种现象叫做共振。
(2)共振曲线直观地反映了物体做受迫振动的振幅与驱动力频率的关系。
①当驱动力的频率f偏离固有频率f0较大时,受迫振动的振幅较小;
②当驱动力的频率f等于固有频率f0时,受迫振动的振幅最大;
③共振曲线上除峰值外,其他某一振幅都对应两个驱动力频率。
5.共振的应用与防止
(1)应用实例:共振筛、共鸣箱
共振筛
共鸣箱
1940年,美国的全长860米的塔柯姆大桥因大风引起的共振而塌毁。
(2)共振的防止
①在桥梁、码头等各种建筑的设计施工中,以及飞机、汽车、轮船的发动机等机器设备的设计、制造、安装中,都必须考虑防止共振产生的危害,以保证建筑和设备的安全。
②防止实例:
机器运转时为了防止共振要调节转速
在振动物体底座加防振垫
军队或火车过桥时要放慢速度或便步走。
例2.如图所示,曲轴上挂一个弹簧振子,转动摇把,曲轴可带动弹簧振子上下振动。开始时不转动摇把,让振子自由振动,测得其频率为2Hz。现匀速转动摇把,转速为240r/min。则( )
A.当振子稳定振动时,它的振动周期是0.5s
B.当振子稳定振动时,它的振动频率是4Hz
C.当转速增大时,弹簧振子的振幅增大
D.当转速减小时,弹簧振子的振幅不变
B
变式训练:一个单摆做受迫振动,其共振曲线(振幅A与驱动力的频率f的关系)如图所示,则( )
A.此单摆的固有周期约为0.5s
B.此单摆的摆长约为2m
C.若摆长增大,单摆的固有频率增大
D.若将此单摆由山脚移至山顶,共振曲线的
峰将略微向左移动
D
技法点拨:
(1)当驱动力频率等于物体固有频率时,物体振动的振幅最大;
(2)当固有频率不等于驱动力频率时,二者越接近,振幅越大,二者相差越大,振幅越小;
(3)单摆的振动周期T=2π????????随摆长和重力加速度的变化而变化。
?
受迫振动 共振
振动中的能量损失
受迫振动:在驱动力作用下的振动。
阻尼振动:振幅逐渐减小
振动系统能量衰减方式
受迫振动
共振
产生共振的条件
共振的防止和应用
再见
学习重点:受迫振动时其频率跟驱动力频率的关系,共振。
学习难点:受迫振动时其频率跟驱动力频率的关系。
思考:你知道为什么大钟会无缘无故地鸣响吗?
东汉以后三国纷争年代,有一天,魏都洛阳宫殿前面的一口大钟,突然无缘无故地鸣响起来,满朝文武议论纷纷,有的以为是不祥之兆,也有人乘机献媚,把它说成是祥瑞。
一、振动中的能量损失
1. 固有振动
思考:让单摆、弹簧振子自由振动,忽略空气阻力,则单摆,弹簧振子做什么运动?
单摆,弹簧振子做简谐运动,周期或频率与振幅无关,仅由系统自身的性质决定。
(1)固有振动:简谐运动的周期或频率与振幅无关,仅由系统自身的性质决定,我们把这种振动称为固有振动。?
(2)固有频率:物体固有振动时的频率仅有系统自身的性质决定,称固有频率。
2.阻尼振动
(2)实际的振动一定是阻尼振动。
(1)阻尼振动:振幅随时间逐渐减小的振动称为阻尼振动。
摇曳的树叶会停下来,摆动的秋千也会停止运动。
思考:阻尼振动中你知道振动系统能量衰减的方式是有哪些吗?
由于实际的振动系统都会受到摩擦力、黏滞力等阻碍作用,振幅必然逐渐减小。
(3)振动系统能量衰减的两种方式
①一种是由于振动系统受到摩擦阻力的作用,使振动系统的机械能逐渐转化为内能。
例如单摆运动时受到空气的阻力。
②另一种是由于振动系统引起邻近介质中各质点的振动,使能量向四周
辐射出去,从而自身机械能减少。
例如音叉发声时,一部分机械能随声波辐射到周围空间,导致音叉振幅减小。
特别提醒!
(1)振动系统受到的阻尼越大,振幅减小得越快,阻尼过大时,系统将不能发生振动。
(2)阻尼振动的振幅是逐渐减小的,但是它的频率是不发生变化的,频率与振幅是无关的。
思考:阻尼振动最终要停下来,那么怎样才能产生持续的振动呢?
例1.如图所示是某单摆做阻尼振动的振动图线,下列说法正确的是( )
A.振动过程中周期变小
B.摆球P时刻的机械能大于N时刻的
机械能
C.摆球P时刻的动能等于N时刻的动能
D.小球在P时刻和N时刻,受到绳子拉
力的大小相等
B
【答案】B
【详解】
A.阻尼振动的周期不变,振幅减小,故A错误;
BC.由于阻力影响,单摆要克服阻力做功,在运动过程中机械能一直逐渐减小,故P时刻的机械能大于N时刻的机械能,而两点重力势能相等,则P时刻的动能大于N时刻的动能,故B正确,C错误;
D.因为PN两时刻位置关于平衡位置对称,但是速度不等,则两时刻受到绳子的拉力大小不相等,故D错误;
故选B。
变式训练:如图所示是单摆做阻尼振动的位移—时间图线,下列说法中正确的是( )
A.摆球在P与N时刻的势能相等
B.摆球在P与N时刻的动能相等
C.摆球在P与N时刻的机械能相等
D.摆球在P时刻的机械能小于在N时刻的机械能
A
技法点拨:
(1)摆球的势能大小由其位移和摆球质量共同决定,由图可知P、N两时刻位移大小相同,则可判断出摆球的势能大小。
(2)机械能E等于动能Ek和势能Ep之和, 阻尼振动中,由于系统机械能在减少E减小, P、N两时刻势能相同,则P时刻动能大于N时刻动能。
产生持续的振动最简单的办法是使周期性的外力作用于振动系统,外力对系统做功,补偿系统的能量损耗,使系统的振动维持下去。
1.驱动力
对振动系统施加的周期性的外力,这种周期性的外力叫作驱动力。
2.受迫振动
系统在驱动力作用下的振动,叫作受迫振动。
机器运转时底座发生的振动、扬声器纸盆的振动,都是受迫振动。
二、受迫振动
实验:研究受迫振动的频率
如图 ,架子上面的电动机向下面的两组弹簧—钩码系统施加周期性的驱动力,使钩码做受迫振动。
改变电动机的转速可以调整驱动力的频率。
思考:物体做受迫振动时,振动稳定后的频率与什么有关?受迫振动物体的频率由什么决定?
(1)接通电源,使钩码做受迫振动,观察记录驱动力的频率和钩码振动的频率。
(2)改变驱动力的频率,再做记录。
研究受迫振动的频率视频
实验结论:
(1)物体做受迫振动达到稳定后,物体振动的频率等于驱动力的频率,与物体的固有频率无关。
(2)驱动力的频率与系统的固有频率相差越少,振幅越大,相差越多,振幅越小。
3.共振现象及其应用
做一做:如图,铁架横梁上挂着几个摆长不同的摆。
其中,A 与 D、G 的摆长相同,D 的摆球质量大于其他摆球。使 D 摆偏离平衡位置后释放,D 摆在振动中通过横梁对其他几个摆施加周期性的驱动力。在振动稳定后比较各球的振幅。
A
D
G
C
E
小球共振实验视频
(1)实验现象:通过观察会发现,固有频率与D摆相同的A摆、G摆振幅最大,固有频率与D摆相差较多的C摆、E摆振幅最小。
(2)实验结论
物体在做受迫振动时,驱动力的频率与物体的固有频率相差越小,受迫振动的振幅越大;当驱动力的频率与物体的固有频率相等时,受迫振动的振幅达到最大。
4.共振
(1)驱动力的频率接近物体的固有频率时,受迫振动的振幅增大,这种现象叫做共振。
(2)共振曲线直观地反映了物体做受迫振动的振幅与驱动力频率的关系。
①当驱动力的频率f偏离固有频率f0较大时,受迫振动的振幅较小;
②当驱动力的频率f等于固有频率f0时,受迫振动的振幅最大;
③共振曲线上除峰值外,其他某一振幅都对应两个驱动力频率。
5.共振的应用与防止
(1)应用实例:共振筛、共鸣箱
共振筛
共鸣箱
1940年,美国的全长860米的塔柯姆大桥因大风引起的共振而塌毁。
(2)共振的防止
①在桥梁、码头等各种建筑的设计施工中,以及飞机、汽车、轮船的发动机等机器设备的设计、制造、安装中,都必须考虑防止共振产生的危害,以保证建筑和设备的安全。
②防止实例:
机器运转时为了防止共振要调节转速
在振动物体底座加防振垫
军队或火车过桥时要放慢速度或便步走。
例2.如图所示,曲轴上挂一个弹簧振子,转动摇把,曲轴可带动弹簧振子上下振动。开始时不转动摇把,让振子自由振动,测得其频率为2Hz。现匀速转动摇把,转速为240r/min。则( )
A.当振子稳定振动时,它的振动周期是0.5s
B.当振子稳定振动时,它的振动频率是4Hz
C.当转速增大时,弹簧振子的振幅增大
D.当转速减小时,弹簧振子的振幅不变
B
变式训练:一个单摆做受迫振动,其共振曲线(振幅A与驱动力的频率f的关系)如图所示,则( )
A.此单摆的固有周期约为0.5s
B.此单摆的摆长约为2m
C.若摆长增大,单摆的固有频率增大
D.若将此单摆由山脚移至山顶,共振曲线的
峰将略微向左移动
D
技法点拨:
(1)当驱动力频率等于物体固有频率时,物体振动的振幅最大;
(2)当固有频率不等于驱动力频率时,二者越接近,振幅越大,二者相差越大,振幅越小;
(3)单摆的振动周期T=2π????????随摆长和重力加速度的变化而变化。
?
受迫振动 共振
振动中的能量损失
受迫振动:在驱动力作用下的振动。
阻尼振动:振幅逐渐减小
振动系统能量衰减方式
受迫振动
共振
产生共振的条件
共振的防止和应用
再见
