4.1.1光的折射 课件—2021-2022学年高二上学期物理人教版(2019)选择性必修第一册(32张PPT)
文档属性
| 名称 | 4.1.1光的折射 课件—2021-2022学年高二上学期物理人教版(2019)选择性必修第一册(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-12 17:06:55 | ||
图片预览







文档简介
4.1.1 光的折射
1.知道光的折射定律;
2.了解光从空气射入水中或其他介质中时的偏折现象以及光路的可逆性;
3.理解折射率的概念,知道折射率越大,介质对光的偏折能力越强,偏折角越大。
学习重点:折射率,光的折射定律。
学习难点:对折射率的理解以及有关计算。
思考:把一块厚玻璃砖放在一支笔的前方,笔杆看起来好像错位了,你认为这是什么原因造成的呢?如何解释观察到的现象?
思考:射水鱼在水中能准确射中水面上不远处的小昆虫。水中的鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?为什么呢?
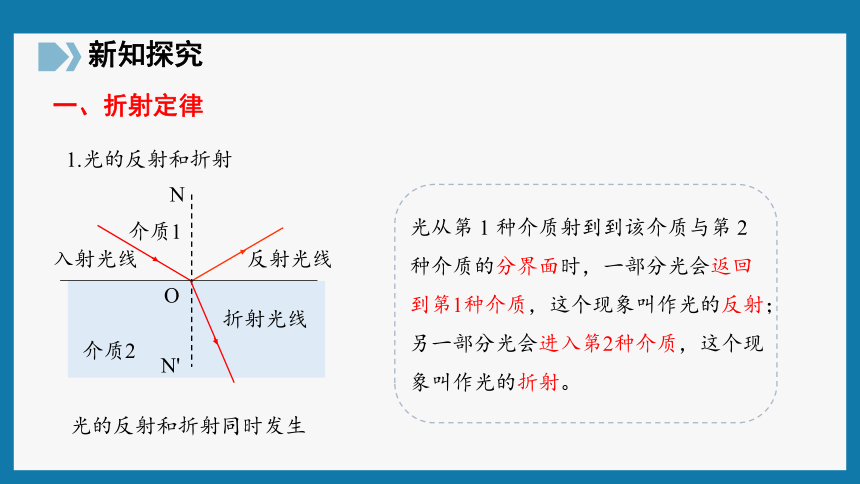
一、折射定律
1.光的反射和折射
光的反射和折射同时发生
入射光线
反射光线
折射光线
N
N'
介质1
介质2
O
光从第 1 种介质射到到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。
光在反射时遵从反射定律,光在折射时遵从什么规律呢?
思考:
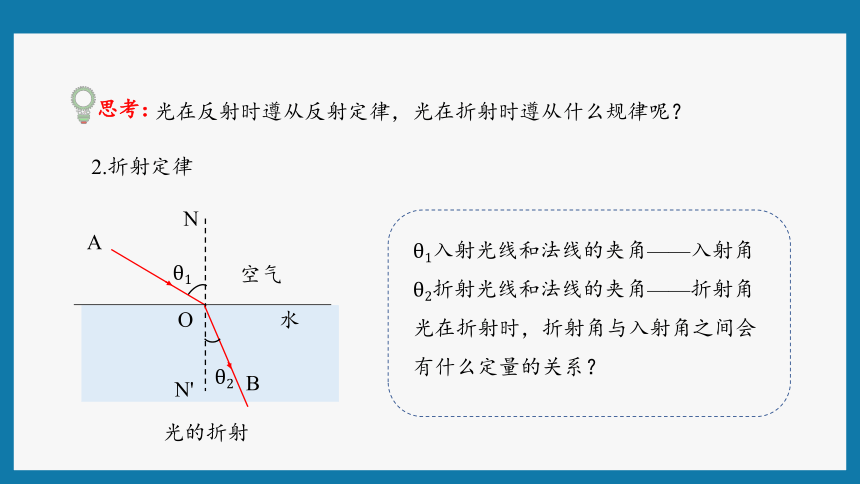
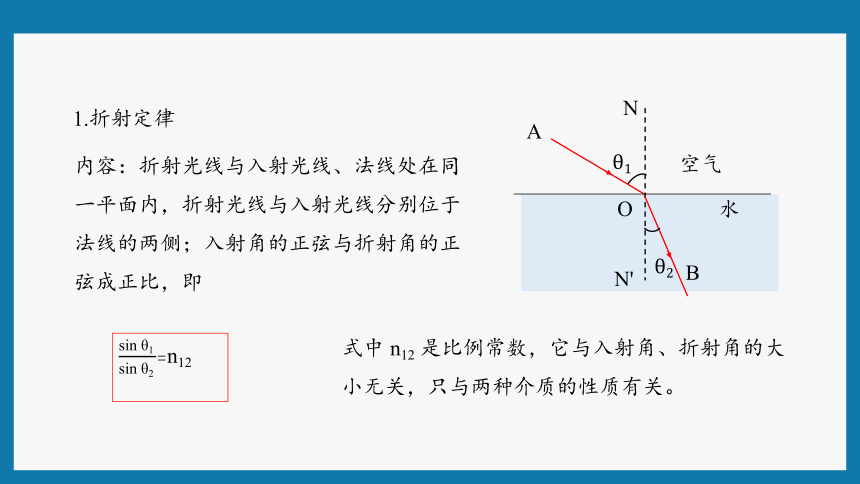
2.折射定律
θ1
?
A
空气
B
N
N'
O
水
θ2
?
光的折射
θ1入射光线和法线的夹角——入射角
θ2折射光线和法线的夹角——折射角
光在折射时,折射角与入射角之间会有什么定量的关系?
?
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律。
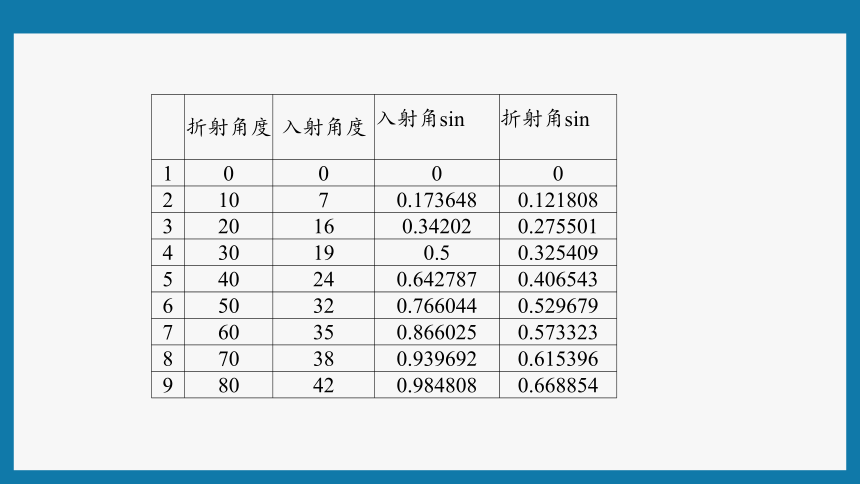
观察实验视频中测量多个入射角和折射角,找出这些数据之间的关系
折射角度
入射角度
入射角sinθ1
折射角sinθ2
1
0
0
0
0
2
10
7
0.173648
0.121808
3
20
16
0.34202
0.275501
4
30
19
0.5
0.325409
5
40
24
0.642787
0.406543
6
50
32
0.766044
0.529679
7
60
35
0.866025
0.573323
8
70
38
0.939692
0.615396
9
80
42
0.984808
0.668854
sinθ1
?
sinθ2
?
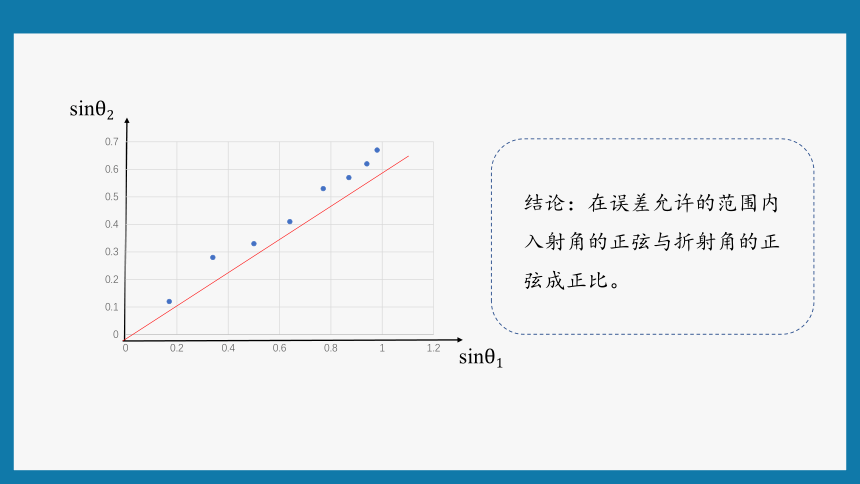
结论:在误差允许的范围内入射角的正弦与折射角的正弦成正比。
1.折射定律
sin?θ1?sin?θ2?=n12
?
式中 n12 是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
θ1
?
A
空气
B
N
N'
O
水
θ2
?
内容:折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即
3.折射角与入射角的大小关系
当光从真空斜射入介质时,入射角大于折射角;当光从介质斜射入真空时,入射角小于折射角;当光垂直射入介质时,光不发生偏折。
2.光路可逆性:在光的反射和折射现象中,光路都是可逆的。
N
N'
介质1
介质2
O
特别提醒
(1)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(2)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
例1.如图所示的四幅图中, 点是半圆形玻璃砖的圆心,一束光由空气进入半圆形玻璃砖,再由玻璃砖射入空气,可能正确的是( )
D.
B.
A.
C.
B
【答案】B
【详解】
AB.当光由空气垂直射入半圆形玻璃砖时,传播方向不发生改变,但由玻璃射向空气时折射角应大于入射角, A错误B正确;
C.光由空气射入半圆形玻璃砖时,折射角应小于入射角, C错误;
D.光由空气垂直射入半圆形玻璃砖时,传播方向不发生改变,D错误。
故选B。
变式训练:
折射现象中,下列说法正确的是( )
A.光从一种介质进入另一种介质时,一定会发生偏折
B.光从空气进入其他介质时,折射角大于入射角
C. 折射角一定小于入射角
D.光从一种介质进入另一种介质时,传播方向并非一定变化
D
技法点拨:
(1)光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(2)折射现象中,折射角和入射角的大小关系与介质的疏密有关系
几种介质的折射率
介质
折射率n
空气
1.0028
水
1.33(4/3)
玻璃
1.50(3/2)
二、折射率
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫作这种介质的绝对折射率,简称折射率,用字母n表示。
2. 真空的折射率为 1,空气的折射率近似为 1。
????=sin?θ1?sin?θ2?
?
sin?θ1表示在真空中的入射角的正弦
sin?θ2表示在介质中折射角的正弦
?
3.物理意义
反映介质的光学性质的物理量。常数 n 越大,光线以相同入射角从真空斜射入这种介质时偏折的角度越大。
4.决定式
(1)某种介质的折射率,等于光在真空中的传播速度c跟光在这种介质中的传播速度v之比。
(2)由于光在真空中的传播速度 c 大于光在任何其他介质中的传播速度 v,因而任何介质的折射率 n 都大于 1。
5.对折射率的理解
(1)入射角和折射角的大小关系取决于两种介质的折射率。
(2)关于正弦值:入射角、折射角是可以改变的,但正弦值之比是一个常数。
(3)关于常数n:不同介质具有不同的常数,常数反映着该介质的光学特性。
(4)决定因素:折射率的大小不仅与介质本身有关,还与光的频率有关。同一种介质中,频率越大的色光折射率越大,传播速度越小。
例如,当白光通过镜折射后,我们可以看到红光偏折最小,紫光偏折最大。说明同一种介质对不同频率f(波长λ)的光,折射率n也不同。其中红光波长较大,频率较小,折射率小。
另外,根据 ,
不同频率f(波长λ)的光在同一介质中传播速度不一样,红光折射率较小,波速v较大。
6.光从真空射入任何介质时,sin θ1 都大于 sin θ2 ,即入射角总是大于折射角。
几种介质的折射率(λ = 589.3 nm t = 20 ℃)
{5940675A-B579-460E-94D1-54222C63F5DA}介质
折射率
介质
折射率
金刚石
2.42
氯化钠
1.54
二硫化碳
1.63
酒精
1.36
玻璃
1.5~ 1.8
水
1.33
水晶
1.55
空气
1.000 28
7.生活中的折射现象
(1)笔杆看起来好像“错位”
这种现象是光的折射引起的。光线通过玻璃砖进入空气发生两次折射:第一次是从空气斜射进入玻璃砖,折射光线应该靠近法线偏折,折射角小于入射角;第二次是从玻璃砖斜射进入空气,折射光线应该远离法
线偏折,折射角大于入射角,所以看上去钢笔似乎被分成了三段,发现钢笔“错位”了。
(2)人在水上看到物体的像,比实际物体位置偏上,感觉水比较浅。鱼在水下看岸上物体的像,比实际物体位置偏上,感觉物体变高。
例1.如图 ,一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB 方向看去,恰好看到桶底上的点C,C、B两点相距d/4。求油的折射率和光在油中传播的速度。
甲 没有油时刚好看到 B 点
乙 有油时沿同一方向看去可以看到 C 点
分析:在图乙中过直线 AB 与油面的交点 O 作油面的垂线,交桶底于 N′点。根据题意可知,来自 C 点的光线沿 CO 到达油面后沿 OA 方向射入空气。折射现象中光路是可逆的,因此如果光线沿AO 方向由空气射到油面,折射光线将沿OC 进入油中。以∠AON 作为入射角,以∠CON′作为折射角,由折射定律可以求出油的折射率 n。
解 因为底面直径与桶高相等,所以
∠AON =∠BON′= 45?
由 ON′= 2CN′可知
sin ∠CON′= CN′?CN′2+?ON′2?=1?5?
?
n = sin?∠AONsin?∠CON′??=2?2?1?5?=5?2?= 1.58
?
因为n =cv ,所以光在油中的传播速度
v =cn =3.0×108?1.58? m/s = 1.9×108 m/s
?
因此,油的折射率
变式训练:关于折射率,下列说法中正确的是( )
A.根据n= sin?θ1?sin?θ2?=可知,介质的折射率与入射角的正弦成正比
B.根据nsin?θ1?sin?θ2?可知,介质的折射率可能为任何正数
C.根据n= ?????v可知,介质的折射率等于光在真空中的传播速度c跟光在这种介质中的传播速度v之比
D.以上说法都不对
?
C
技法点拨:
介质的折射率n与入射角的正弦和折射角的正弦无关,介质的折射率等于光在真空中的传播速度c跟光在这种介质中的传播速度v之, 介质的折射率一定大于1。
光的折射
折射定律
折射定律的表达式
折射定律内容
sin?θ1?sin?θ2?=n12
?
折射率
在光的折射或反射现象中,光路都是可逆的。
????=sin?θ1?sin?θ2?
?
从真空射入某种介质发生折射时
反映介质的光学性质的物理量
折射率与光速的关系:n =cv,由于c>v,故任何介质的折射率n都大于1。
?
再见
1.知道光的折射定律;
2.了解光从空气射入水中或其他介质中时的偏折现象以及光路的可逆性;
3.理解折射率的概念,知道折射率越大,介质对光的偏折能力越强,偏折角越大。
学习重点:折射率,光的折射定律。
学习难点:对折射率的理解以及有关计算。
思考:把一块厚玻璃砖放在一支笔的前方,笔杆看起来好像错位了,你认为这是什么原因造成的呢?如何解释观察到的现象?
思考:射水鱼在水中能准确射中水面上不远处的小昆虫。水中的鱼看到小昆虫在什么位置?是在昆虫的上方还是下方?为什么呢?
一、折射定律
1.光的反射和折射
光的反射和折射同时发生
入射光线
反射光线
折射光线
N
N'
介质1
介质2
O
光从第 1 种介质射到到该介质与第 2 种介质的分界面时,一部分光会返回到第1种介质,这个现象叫作光的反射;另一部分光会进入第2种介质,这个现象叫作光的折射。
光在反射时遵从反射定律,光在折射时遵从什么规律呢?
思考:
2.折射定律
θ1
?
A
空气
B
N
N'
O
水
θ2
?
光的折射
θ1入射光线和法线的夹角——入射角
θ2折射光线和法线的夹角——折射角
光在折射时,折射角与入射角之间会有什么定量的关系?
?
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律。
观察实验视频中测量多个入射角和折射角,找出这些数据之间的关系
折射角度
入射角度
入射角sinθ1
折射角sinθ2
1
0
0
0
0
2
10
7
0.173648
0.121808
3
20
16
0.34202
0.275501
4
30
19
0.5
0.325409
5
40
24
0.642787
0.406543
6
50
32
0.766044
0.529679
7
60
35
0.866025
0.573323
8
70
38
0.939692
0.615396
9
80
42
0.984808
0.668854
sinθ1
?
sinθ2
?
结论:在误差允许的范围内入射角的正弦与折射角的正弦成正比。
1.折射定律
sin?θ1?sin?θ2?=n12
?
式中 n12 是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
θ1
?
A
空气
B
N
N'
O
水
θ2
?
内容:折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即
3.折射角与入射角的大小关系
当光从真空斜射入介质时,入射角大于折射角;当光从介质斜射入真空时,入射角小于折射角;当光垂直射入介质时,光不发生偏折。
2.光路可逆性:在光的反射和折射现象中,光路都是可逆的。
N
N'
介质1
介质2
O
特别提醒
(1)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(2)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
例1.如图所示的四幅图中, 点是半圆形玻璃砖的圆心,一束光由空气进入半圆形玻璃砖,再由玻璃砖射入空气,可能正确的是( )
D.
B.
A.
C.
B
【答案】B
【详解】
AB.当光由空气垂直射入半圆形玻璃砖时,传播方向不发生改变,但由玻璃射向空气时折射角应大于入射角, A错误B正确;
C.光由空气射入半圆形玻璃砖时,折射角应小于入射角, C错误;
D.光由空气垂直射入半圆形玻璃砖时,传播方向不发生改变,D错误。
故选B。
变式训练:
折射现象中,下列说法正确的是( )
A.光从一种介质进入另一种介质时,一定会发生偏折
B.光从空气进入其他介质时,折射角大于入射角
C. 折射角一定小于入射角
D.光从一种介质进入另一种介质时,传播方向并非一定变化
D
技法点拨:
(1)光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(2)折射现象中,折射角和入射角的大小关系与介质的疏密有关系
几种介质的折射率
介质
折射率n
空气
1.0028
水
1.33(4/3)
玻璃
1.50(3/2)
二、折射率
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫作这种介质的绝对折射率,简称折射率,用字母n表示。
2. 真空的折射率为 1,空气的折射率近似为 1。
????=sin?θ1?sin?θ2?
?
sin?θ1表示在真空中的入射角的正弦
sin?θ2表示在介质中折射角的正弦
?
3.物理意义
反映介质的光学性质的物理量。常数 n 越大,光线以相同入射角从真空斜射入这种介质时偏折的角度越大。
4.决定式
(1)某种介质的折射率,等于光在真空中的传播速度c跟光在这种介质中的传播速度v之比。
(2)由于光在真空中的传播速度 c 大于光在任何其他介质中的传播速度 v,因而任何介质的折射率 n 都大于 1。
5.对折射率的理解
(1)入射角和折射角的大小关系取决于两种介质的折射率。
(2)关于正弦值:入射角、折射角是可以改变的,但正弦值之比是一个常数。
(3)关于常数n:不同介质具有不同的常数,常数反映着该介质的光学特性。
(4)决定因素:折射率的大小不仅与介质本身有关,还与光的频率有关。同一种介质中,频率越大的色光折射率越大,传播速度越小。
例如,当白光通过镜折射后,我们可以看到红光偏折最小,紫光偏折最大。说明同一种介质对不同频率f(波长λ)的光,折射率n也不同。其中红光波长较大,频率较小,折射率小。
另外,根据 ,
不同频率f(波长λ)的光在同一介质中传播速度不一样,红光折射率较小,波速v较大。
6.光从真空射入任何介质时,sin θ1 都大于 sin θ2 ,即入射角总是大于折射角。
几种介质的折射率(λ = 589.3 nm t = 20 ℃)
{5940675A-B579-460E-94D1-54222C63F5DA}介质
折射率
介质
折射率
金刚石
2.42
氯化钠
1.54
二硫化碳
1.63
酒精
1.36
玻璃
1.5~ 1.8
水
1.33
水晶
1.55
空气
1.000 28
7.生活中的折射现象
(1)笔杆看起来好像“错位”
这种现象是光的折射引起的。光线通过玻璃砖进入空气发生两次折射:第一次是从空气斜射进入玻璃砖,折射光线应该靠近法线偏折,折射角小于入射角;第二次是从玻璃砖斜射进入空气,折射光线应该远离法
线偏折,折射角大于入射角,所以看上去钢笔似乎被分成了三段,发现钢笔“错位”了。
(2)人在水上看到物体的像,比实际物体位置偏上,感觉水比较浅。鱼在水下看岸上物体的像,比实际物体位置偏上,感觉物体变高。
例1.如图 ,一个储油桶的底面直径与高均为d。当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB 方向看去,恰好看到桶底上的点C,C、B两点相距d/4。求油的折射率和光在油中传播的速度。
甲 没有油时刚好看到 B 点
乙 有油时沿同一方向看去可以看到 C 点
分析:在图乙中过直线 AB 与油面的交点 O 作油面的垂线,交桶底于 N′点。根据题意可知,来自 C 点的光线沿 CO 到达油面后沿 OA 方向射入空气。折射现象中光路是可逆的,因此如果光线沿AO 方向由空气射到油面,折射光线将沿OC 进入油中。以∠AON 作为入射角,以∠CON′作为折射角,由折射定律可以求出油的折射率 n。
解 因为底面直径与桶高相等,所以
∠AON =∠BON′= 45?
由 ON′= 2CN′可知
sin ∠CON′= CN′?CN′2+?ON′2?=1?5?
?
n = sin?∠AONsin?∠CON′??=2?2?1?5?=5?2?= 1.58
?
因为n =cv ,所以光在油中的传播速度
v =cn =3.0×108?1.58? m/s = 1.9×108 m/s
?
因此,油的折射率
变式训练:关于折射率,下列说法中正确的是( )
A.根据n= sin?θ1?sin?θ2?=可知,介质的折射率与入射角的正弦成正比
B.根据nsin?θ1?sin?θ2?可知,介质的折射率可能为任何正数
C.根据n= ?????v可知,介质的折射率等于光在真空中的传播速度c跟光在这种介质中的传播速度v之比
D.以上说法都不对
?
C
技法点拨:
介质的折射率n与入射角的正弦和折射角的正弦无关,介质的折射率等于光在真空中的传播速度c跟光在这种介质中的传播速度v之, 介质的折射率一定大于1。
光的折射
折射定律
折射定律的表达式
折射定律内容
sin?θ1?sin?θ2?=n12
?
折射率
在光的折射或反射现象中,光路都是可逆的。
????=sin?θ1?sin?θ2?
?
从真空射入某种介质发生折射时
反映介质的光学性质的物理量
折射率与光速的关系:n =cv,由于c>v,故任何介质的折射率n都大于1。
?
再见
