人教版数学八年级上册11.2.1三角形的内角课件 (16张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.2.1三角形的内角课件 (16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 949.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 18:12:23 | ||
图片预览



文档简介
三角形的内角
(第一课时)
检查预习
在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C=
自主学习
问题1:自学教材11页内容,对照书上的拼法将准备好的三角形的角剪下来选择一种拼法拼一拼,并思考还有其它的拼法吗?
问题 2: 将操作过程用画图的形式抽象出来
,看一看你有什么发现,并在小组内交流你的发现。
问题3:各小组派代表上台展示拼法和发现,说一说证明思路。
问题4: 选择一种拼法写出证明过程。
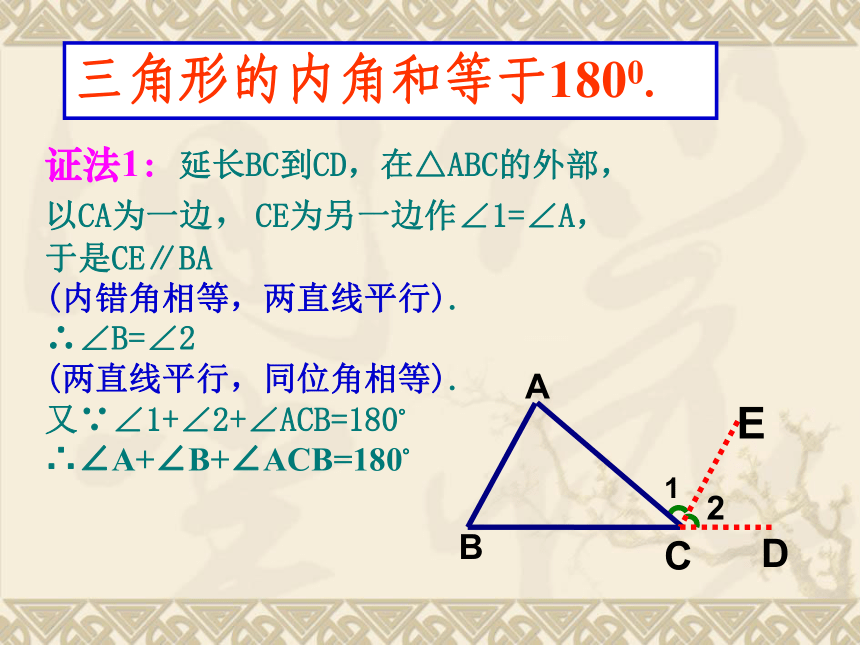
证法1:延长BC到CD,在△ABC的外部,
以CA为一边,CE为另一边作∠1=∠A,
于是CE∥BA
(内错角相等,两直线平行).
∴∠B=∠2
(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
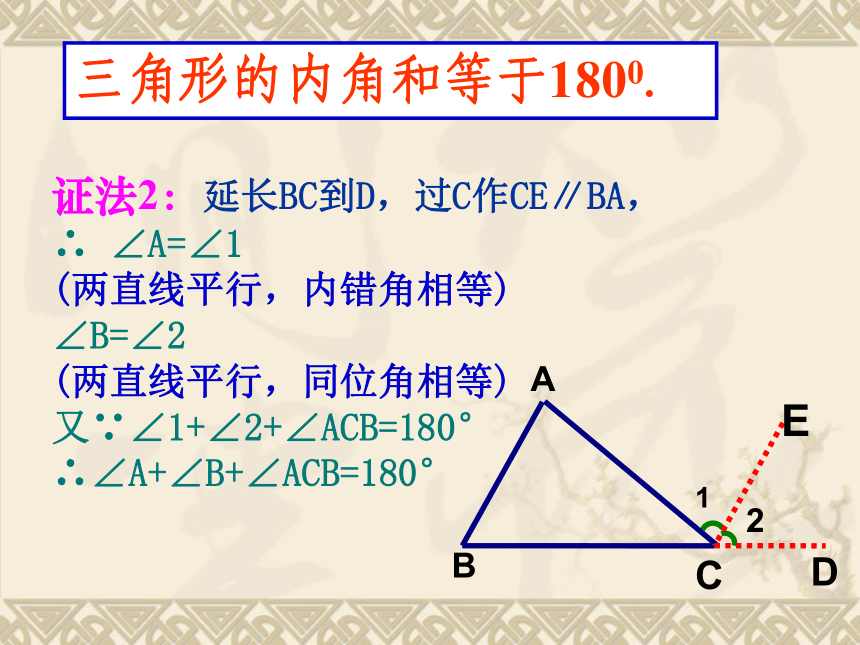
证法2:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
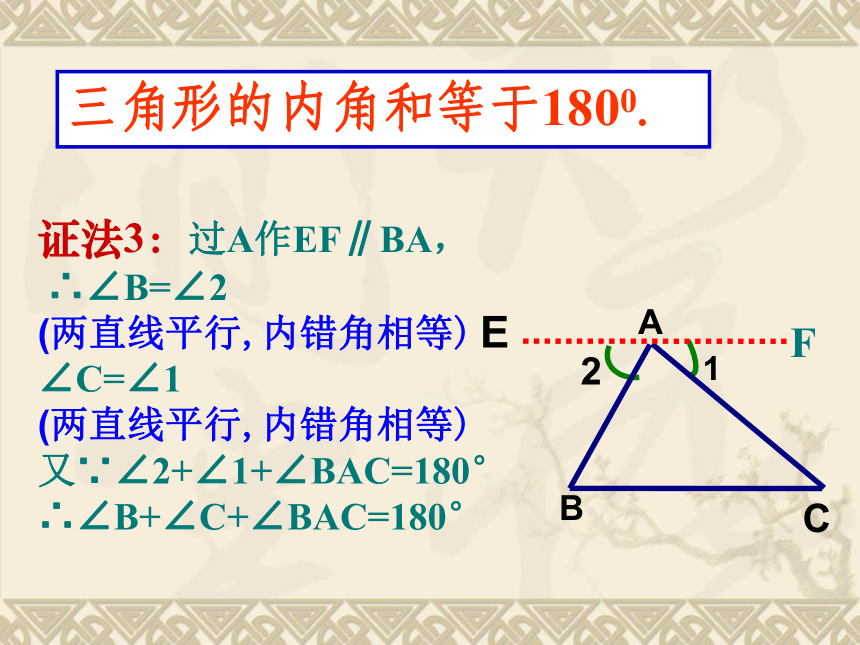
证法3:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
三角形的内角和等于1800.
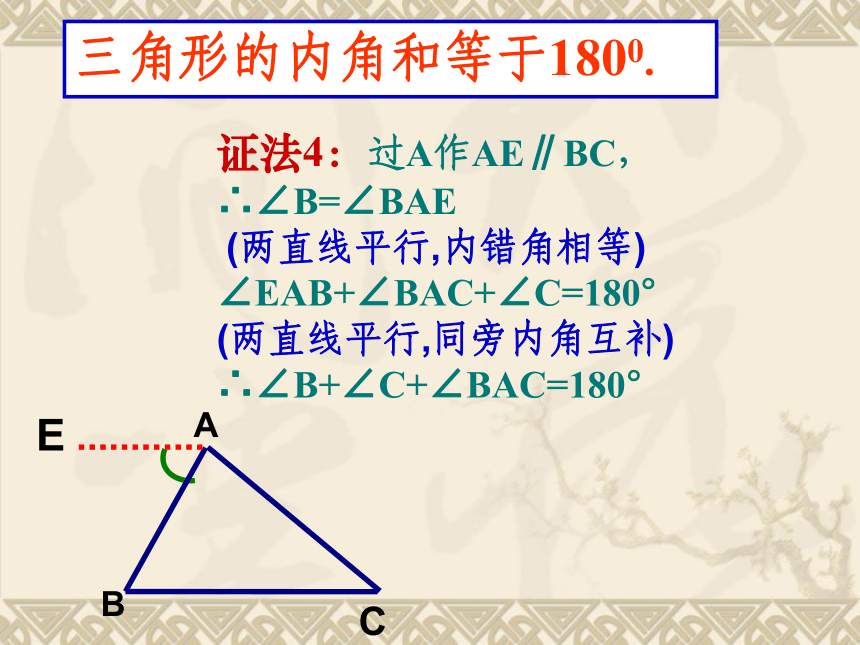
证法4:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
C
B
E
A
三角形的内角和等于1800.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
(1)一个三角形中最多有 个直角?为什么
?
(2)一个三角形中最多有 个钝角?为什么
?
(3)一个三角形中至少有 个锐角?为什么
?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
新知应用
合作探究
例题2. 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
北
.
A
D
北
.
C
B
.
东
E
解:∠CAB= ∠BAD - ∠CAD =80°-50°= 30°
∵AD∥BE,得: ∠BAD +∠BADE=180°
∴ ∠ABE=180°- ∠BAD = 180°- 80°=100°
∠ABC=∠ABE-∠EBC= 100°- 40°=60°
在△ABC中 ,∠ACB= 180°- ∠ABC -∠CAB
= 180°- 60°- 30°= 90°
答:从B岛看A,C两岛的视角∠ABC是60°,从C岛看A、B两岛的视角∠ACB是90°
你还能想出其他办法吗?
?
拓展交流
如图,已知∠1=15°,∠2=30°,∠A=50°,求∠BDC的度数.
课堂小结: 说说自己本节课的收获和体会。
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
C
练习
2、在△ABC中,如果
∠A = ∠B= ∠ C,
那么△ABC是什么三角形?
这节课你有那些收获?
凭勤奋出成果
向效率要质量
(第一课时)
检查预习
在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C=
自主学习
问题1:自学教材11页内容,对照书上的拼法将准备好的三角形的角剪下来选择一种拼法拼一拼,并思考还有其它的拼法吗?
问题 2: 将操作过程用画图的形式抽象出来
,看一看你有什么发现,并在小组内交流你的发现。
问题3:各小组派代表上台展示拼法和发现,说一说证明思路。
问题4: 选择一种拼法写出证明过程。
证法1:延长BC到CD,在△ABC的外部,
以CA为一边,CE为另一边作∠1=∠A,
于是CE∥BA
(内错角相等,两直线平行).
∴∠B=∠2
(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
证法2:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
证法3:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
三角形的内角和等于1800.
证法4:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
C
B
E
A
三角形的内角和等于1800.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
(1)一个三角形中最多有 个直角?为什么
?
(2)一个三角形中最多有 个钝角?为什么
?
(3)一个三角形中至少有 个锐角?为什么
?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
新知应用
合作探究
例题2. 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
北
.
A
D
北
.
C
B
.
东
E
解:∠CAB= ∠BAD - ∠CAD =80°-50°= 30°
∵AD∥BE,得: ∠BAD +∠BADE=180°
∴ ∠ABE=180°- ∠BAD = 180°- 80°=100°
∠ABC=∠ABE-∠EBC= 100°- 40°=60°
在△ABC中 ,∠ACB= 180°- ∠ABC -∠CAB
= 180°- 60°- 30°= 90°
答:从B岛看A,C两岛的视角∠ABC是60°,从C岛看A、B两岛的视角∠ACB是90°
你还能想出其他办法吗?
?
拓展交流
如图,已知∠1=15°,∠2=30°,∠A=50°,求∠BDC的度数.
课堂小结: 说说自己本节课的收获和体会。
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
C
练习
2、在△ABC中,如果
∠A = ∠B= ∠ C,
那么△ABC是什么三角形?
这节课你有那些收获?
凭勤奋出成果
向效率要质量
