青岛版数学九年级上册3.7 《正多边形与圆》课件(21张PPT)
文档属性
| 名称 | 青岛版数学九年级上册3.7 《正多边形与圆》课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 166.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 00:00:00 | ||
图片预览


文档简介
3.7 正多边形和圆
青岛版九年级(上)数学
正多边形
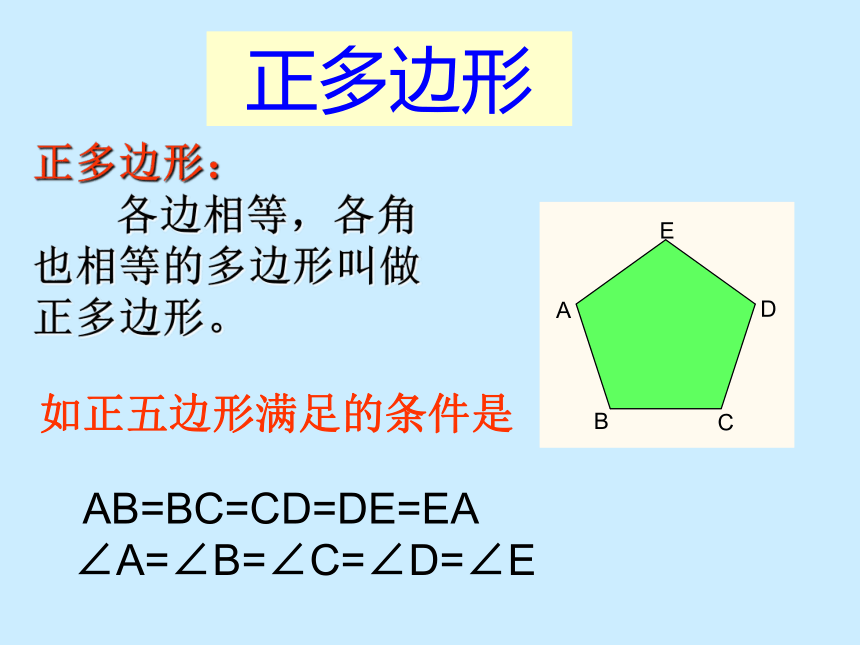
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
AB=BC=CD=DE=EA
∠A=∠B=∠C=∠D=∠E
如正五边形满足的条件是
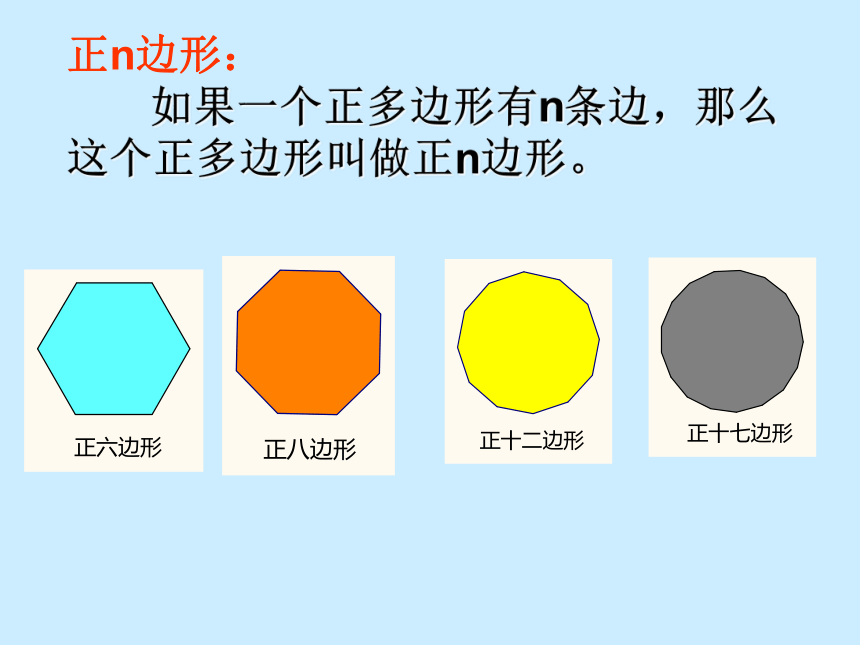
正n边形:
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
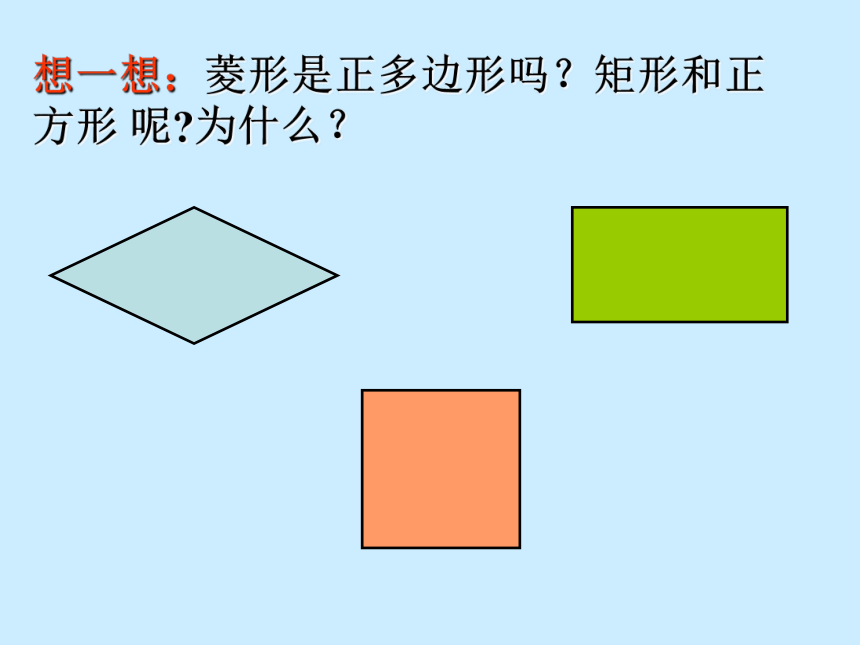
想一想:菱形是正多边形吗?矩形和正方形 呢?为什么?
你知道正多边形和圆有什么关系吗?
正多边形和圆
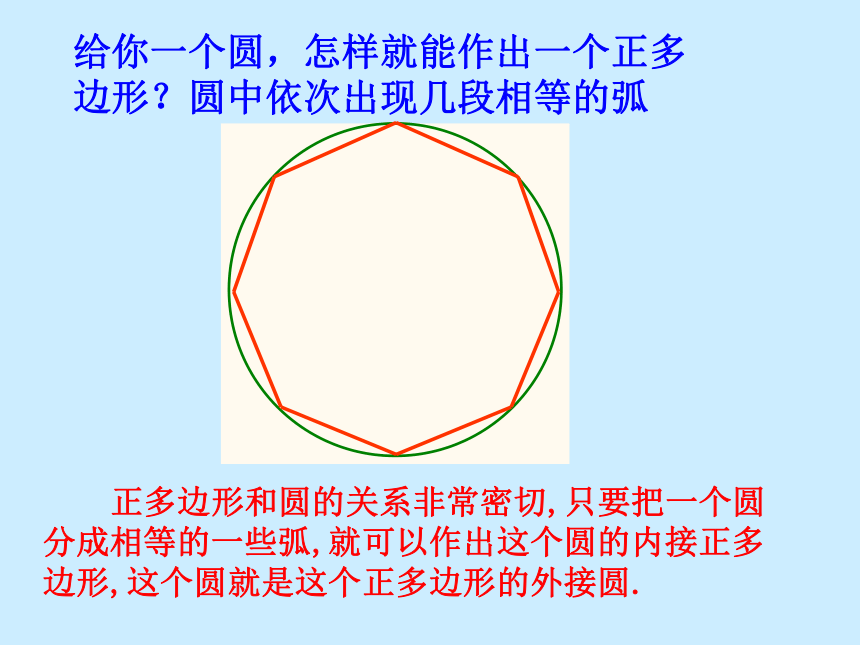
给你一个圆,怎样就能作出一个正多边形?圆中依次出现几段相等的弧
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
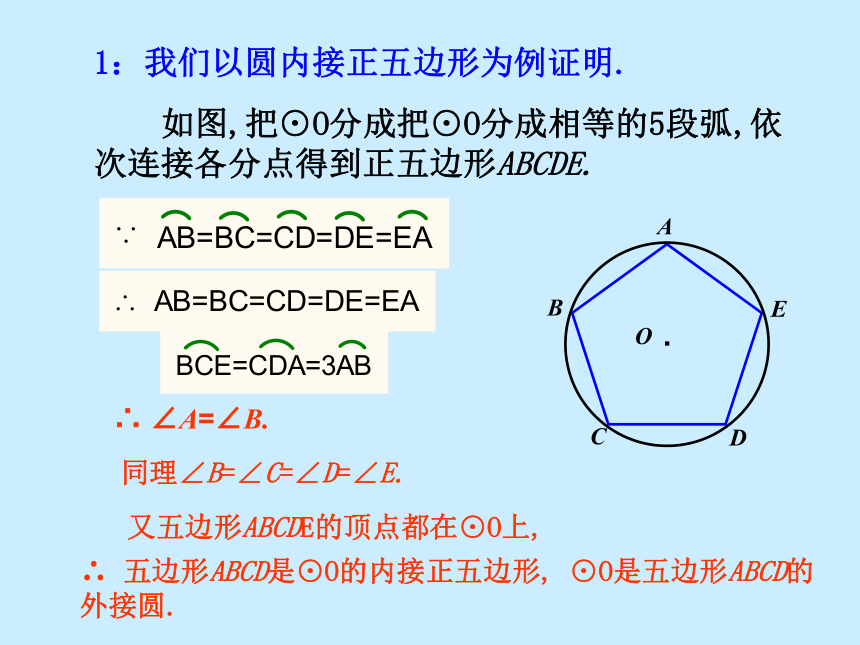
如图,把⊙O分成把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
∴ ∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCD是⊙O的内接正五边形, ⊙O是五边形ABCD的外接圆.
1:我们以圆内接正五边形为例证明.
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
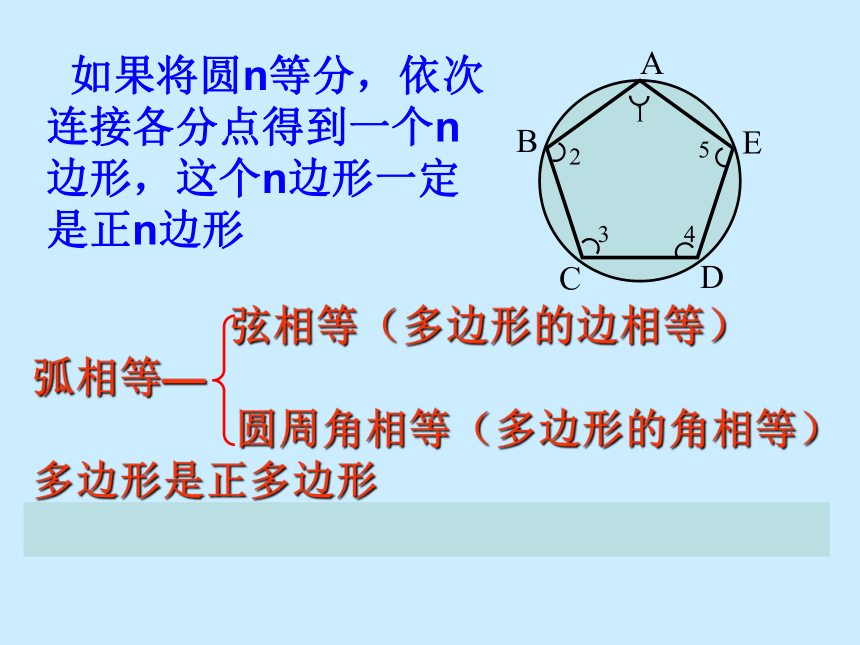
如果将圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等)
多边形是正多边形
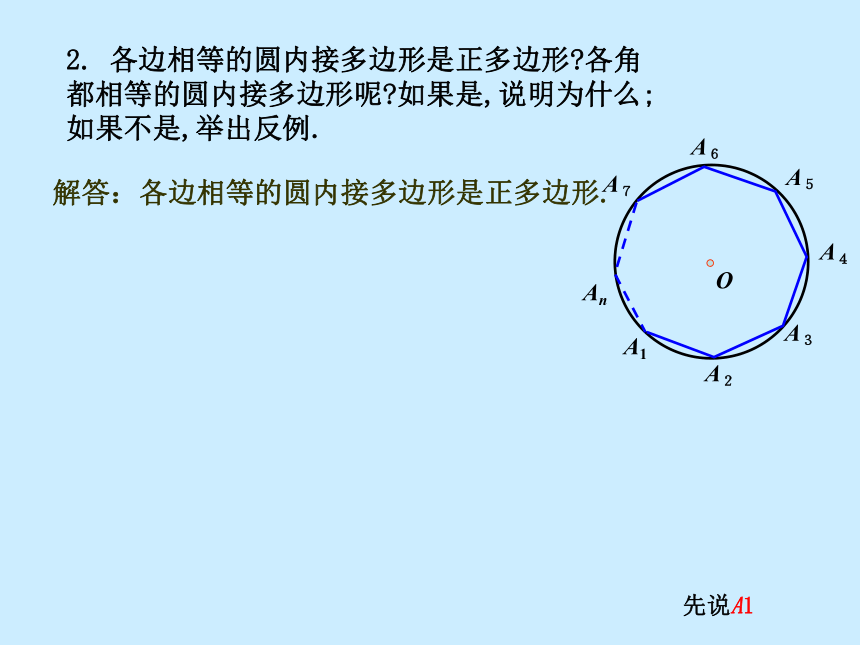
2. 各边相等的圆内接多边形是正多边形?各角都相等的圆内接多边形呢?如果是,说明为什么;如果不是,举出反例.
解答:各边相等的圆内接多边形是正多边形.
·
A1
A2
A3
A4
A5
A6
A7
An
O
先说A1
正多边形每一边所对的圆心角叫做正多边形的中心角.
O
·
中心角
半径R
边心距r
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.
外接圆的半径叫做正多边形的半径.
中心到正多边形的距离叫做正多边形的边心距.
我们在以前学过了那些正多边形?
请同学们找出它们的中心,画出它们的半径,边心距和中心角!
(等边三角形,正方形等)
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
例 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l =4×6=24(m).
在Rt△OPC中,OC=4, PC=
利用勾股定理,可得边心距
亭子地基的面积
O
A
B
C
D
E
F
R
P
r
请同学们完成下表中有关正多边形的计算
正多边形边数
内角
中心角
半径
边长
边心距
周长
面积
3
4
6
1
60°
90°
120°
120°
90°
60°
2
4
2
2
12
8
2
1
抢答题:
1、O是正
圆与 圆的圆心。
△ABC的中心,它是△ABC的
2、OB叫正△ABC的 ,它是正△ABC的 圆的半径。
3、OD叫作正△ABC的 ,它是正△ABC的 圆的半径。
A
B
C
.O
D
外接
内切
半径
外接
边心距
内切
4、正方形ABCD的外接圆圆心O叫做
正方形ABCD的 ;
5、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的 .
A
B
C
D
.O
E
中心
边心距
6、⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。
7、 ∠AOB叫做正五边形ABCDE的 角,
它的度数是
D
E
A
B
C
.O
F
边心距
内切
中心
72°
8、图中正六边形ABCDEF的中心角是
它的度数是
9、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么?
B
A
E
F
C
D
.O
∠AOB
60°
3.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
连接OB,则OB=R
在Rt△OBD中 ∠OBD=30°,
边心距=OD=
·
A
B
C
D
O
\BC =2 BD = 3 R
在Rt△OBD中 由勾股定理得:
BD= OB2-BD2 = R2 - ( )2 =
3
2
R
S△ABC = - BC×AD = - × 3 R × - R = R2
3.
3
4
3
2
2
1
2
1
解:连接OB,OC 作OE⊥BC垂足为E,
∠OEB=90° ∠OBE= ∠ BOE=45°
在Rt△OBE中为等腰直角三角形
·
A
B
C
D
O
E
反思总结,拓展升华
1,本节课你学习了什么?
2, 正n边形的一个内角的度数是多少?中心角呢?
3,正多边形的中心角与外角的大小有什么关系?
4,正多边形有那些性质?
5,正n边形的半径,边心距,边长有什么关系?
作业:教材习题116页,1、2、4、6、7题
再见
青岛版九年级(上)数学
正多边形
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
AB=BC=CD=DE=EA
∠A=∠B=∠C=∠D=∠E
如正五边形满足的条件是
正n边形:
如果一个正多边形有n条边,那么这个正多边形叫做正n边形。
想一想:菱形是正多边形吗?矩形和正方形 呢?为什么?
你知道正多边形和圆有什么关系吗?
正多边形和圆
给你一个圆,怎样就能作出一个正多边形?圆中依次出现几段相等的弧
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
如图,把⊙O分成把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
∴ ∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCD是⊙O的内接正五边形, ⊙O是五边形ABCD的外接圆.
1:我们以圆内接正五边形为例证明.
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
如果将圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等)
多边形是正多边形
2. 各边相等的圆内接多边形是正多边形?各角都相等的圆内接多边形呢?如果是,说明为什么;如果不是,举出反例.
解答:各边相等的圆内接多边形是正多边形.
·
A1
A2
A3
A4
A5
A6
A7
An
O
先说A1
正多边形每一边所对的圆心角叫做正多边形的中心角.
O
·
中心角
半径R
边心距r
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.
外接圆的半径叫做正多边形的半径.
中心到正多边形的距离叫做正多边形的边心距.
我们在以前学过了那些正多边形?
请同学们找出它们的中心,画出它们的半径,边心距和中心角!
(等边三角形,正方形等)
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
例 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
解: 如图由于ABCDEF是正六边形,所以它的中心角等于 ,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此,亭子地基的周长
l =4×6=24(m).
在Rt△OPC中,OC=4, PC=
利用勾股定理,可得边心距
亭子地基的面积
O
A
B
C
D
E
F
R
P
r
请同学们完成下表中有关正多边形的计算
正多边形边数
内角
中心角
半径
边长
边心距
周长
面积
3
4
6
1
60°
90°
120°
120°
90°
60°
2
4
2
2
12
8
2
1
抢答题:
1、O是正
圆与 圆的圆心。
△ABC的中心,它是△ABC的
2、OB叫正△ABC的 ,它是正△ABC的 圆的半径。
3、OD叫作正△ABC的 ,它是正△ABC的 圆的半径。
A
B
C
.O
D
外接
内切
半径
外接
边心距
内切
4、正方形ABCD的外接圆圆心O叫做
正方形ABCD的 ;
5、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的 .
A
B
C
D
.O
E
中心
边心距
6、⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。
7、 ∠AOB叫做正五边形ABCDE的 角,
它的度数是
D
E
A
B
C
.O
F
边心距
内切
中心
72°
8、图中正六边形ABCDEF的中心角是
它的度数是
9、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么?
B
A
E
F
C
D
.O
∠AOB
60°
3.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
连接OB,则OB=R
在Rt△OBD中 ∠OBD=30°,
边心距=OD=
·
A
B
C
D
O
\BC =2 BD = 3 R
在Rt△OBD中 由勾股定理得:
BD= OB2-BD2 = R2 - ( )2 =
3
2
R
S△ABC = - BC×AD = - × 3 R × - R = R2
3.
3
4
3
2
2
1
2
1
解:连接OB,OC 作OE⊥BC垂足为E,
∠OEB=90° ∠OBE= ∠ BOE=45°
在Rt△OBE中为等腰直角三角形
·
A
B
C
D
O
E
反思总结,拓展升华
1,本节课你学习了什么?
2, 正n边形的一个内角的度数是多少?中心角呢?
3,正多边形的中心角与外角的大小有什么关系?
4,正多边形有那些性质?
5,正n边形的半径,边心距,边长有什么关系?
作业:教材习题116页,1、2、4、6、7题
再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
