青岛版数学九年级上册3.6《 弧长及扇形的面积》课件(21张PPT)
文档属性
| 名称 | 青岛版数学九年级上册3.6《 弧长及扇形的面积》课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 578.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-14 19:55:22 | ||
图片预览



文档简介
第四章: 对圆的进一步认识
4.7弧长及扇形面积的计算
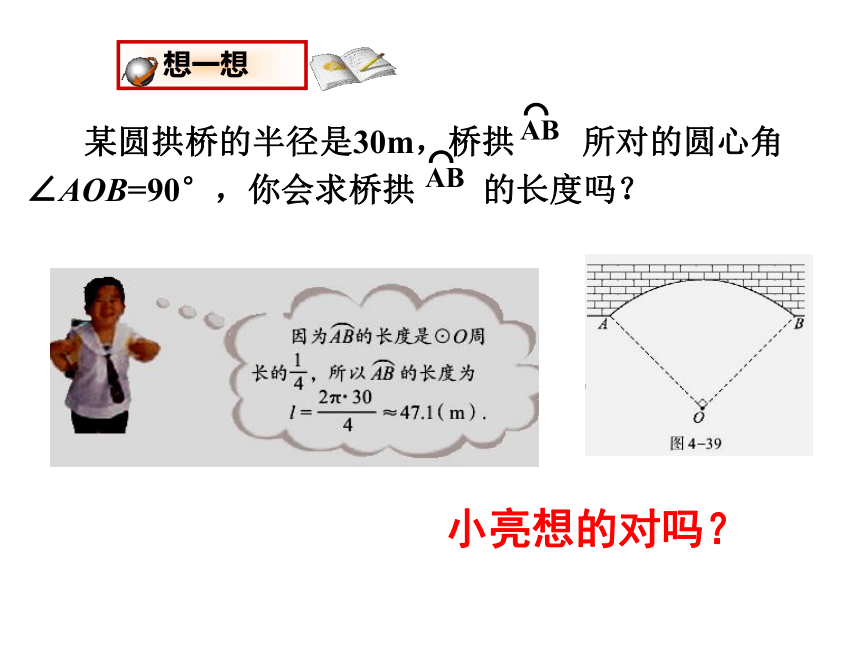
某圆拱桥的半径是30m,桥拱 所对的圆心角
∠AOB=90°,你会求桥拱 的长度吗?
AB
⌒
AB
⌒
小亮想的对吗?
想一想
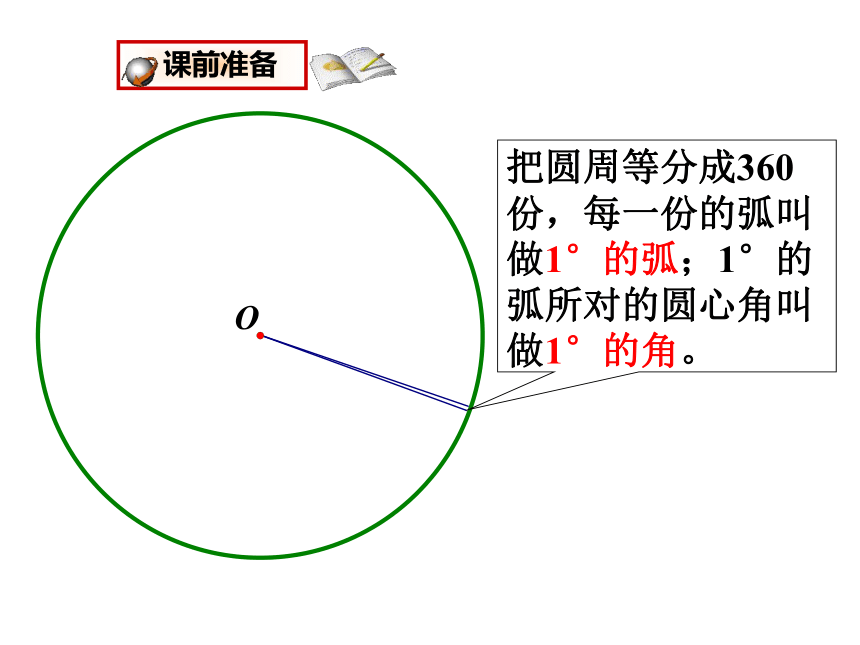
把圆周等分成360份,每一份的弧叫做1°的弧;1°的弧所对的圆心角叫做1°的角。
课前准备
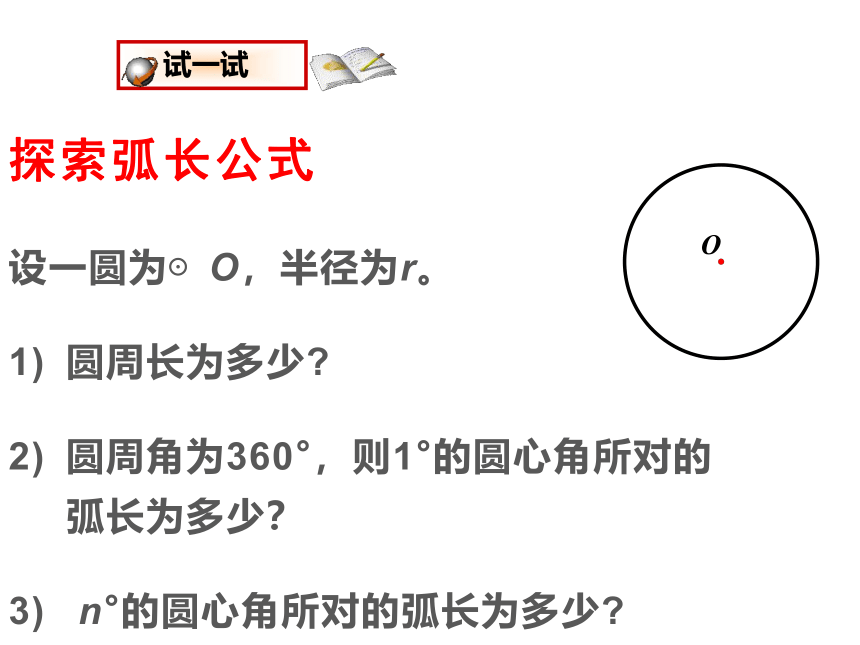
探索弧长公式
设一圆为⊙O,半径为r。
圆周长为多少?
圆周角为360°,则1°的圆心角所对的弧长为多少?
n°的圆心角所对的弧长为多少?
试一试
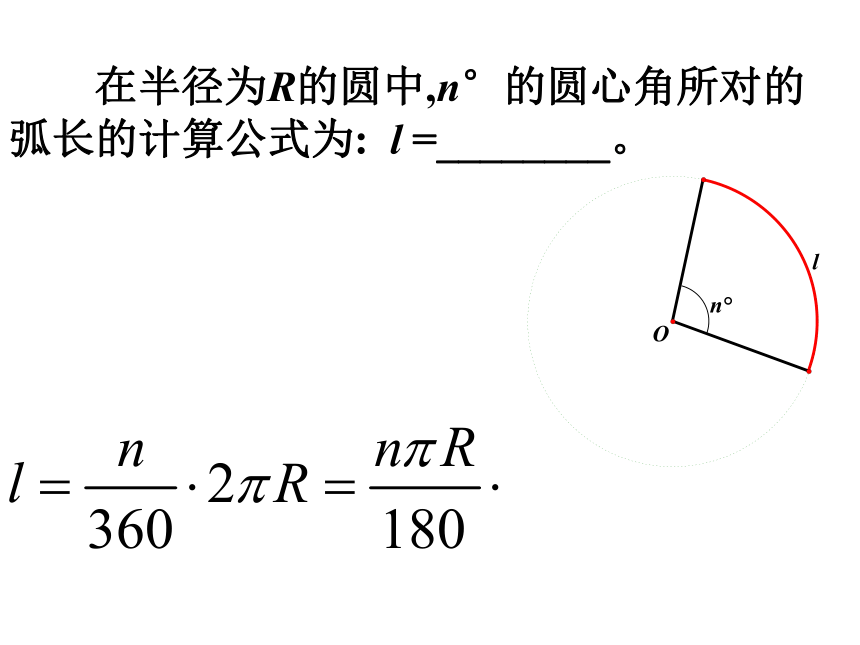
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为: l =________。
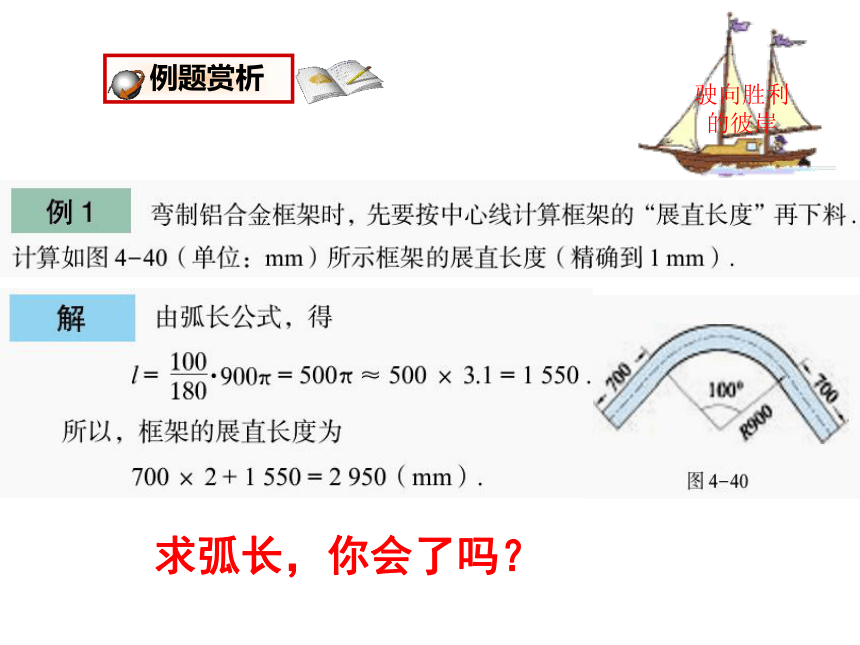
例题赏析
驶向胜利的彼岸
求弧长,你会了吗?
练一练
驶向胜利的彼岸
探索面积公式
设一圆的为⊙O,半径为r。
圆面积为多少?
圆周角为360°,则1°的圆心角所对的扇形面积为多少?
n°的圆心角所对的扇形面积为多少?
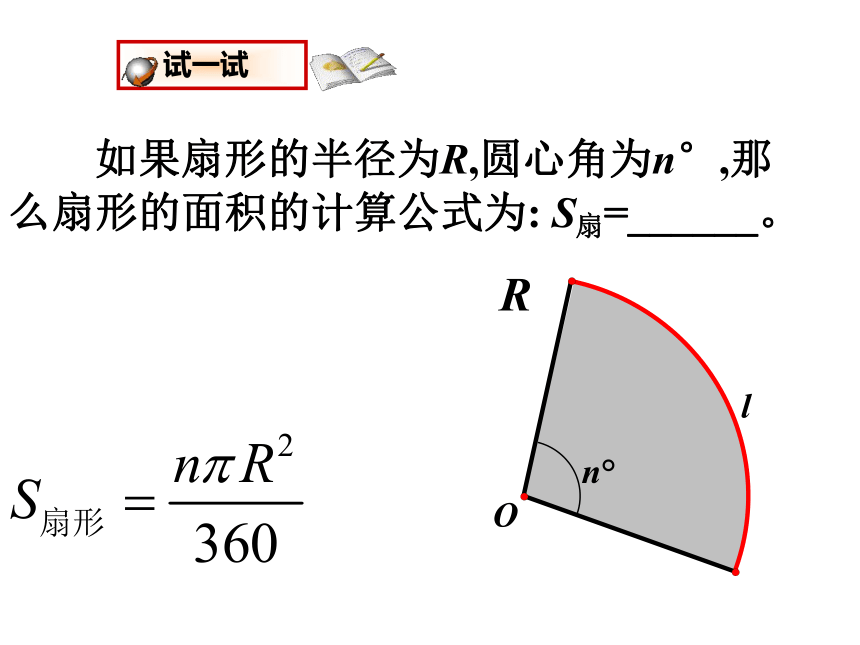
试一试
如果扇形的半径为R,圆心角为n°,那么扇形的面积的计算公式为: S扇=______。
R
试一试
例1:
扇形AOB的半径为30cm,∠AOB=120°,
1、求弧AB的长(结果精确到0.1cm)
2、扇形AOB的面积(结果精确到0.1cm2)
例题赏析
例题赏析
n°
l
O
比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?
探索弧长与扇形面积的关系
S
r
探索发现
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?
跟踪训练
挑战自我
练习1:扇形的面积是S,它的半径是r,求这个扇形的弧长.
练习2:如图,在同心圆中,两圆半径分别为2, 1,∠AOB=120°,求阴影部分的面积.
A
B
O
120°
练一练
B
C
A
⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少?
挑战极限
B
C
A
D
⊙A, ⊙B, ⊙C, ⊙D两两不相交,且半径都是1cm,则图中的四个扇形的面积之和为多少?弧长的和为多少?
挑战极限
⊙A, ⊙B, ⊙C, ⊙D ,⊙E两两不相交,且半径都是1cm,则图中的五个扇形的面积之和为多少?弧长的和为多少?
B
C
A
D
E
若象这样的n个圆呢?
挑战极限
挑战自我
习题4.7 3-2题
祝你成功!
独立作业
驶向胜利的彼岸
结束寄语
形成天才的决定因素应该是勤奋.
下课了!
再见
补充:
如图,某传送带的一个转动轮的半径为10cm.
1)转动轮转一周,传送带上的物品A被传送多少厘米?
2)转动轮转1°,传送带上的物品A被传送多少厘米?
3)转动轮转n°,传送带上的物品A被传送多少厘米?
4.7弧长及扇形面积的计算
某圆拱桥的半径是30m,桥拱 所对的圆心角
∠AOB=90°,你会求桥拱 的长度吗?
AB
⌒
AB
⌒
小亮想的对吗?
想一想
把圆周等分成360份,每一份的弧叫做1°的弧;1°的弧所对的圆心角叫做1°的角。
课前准备
探索弧长公式
设一圆为⊙O,半径为r。
圆周长为多少?
圆周角为360°,则1°的圆心角所对的弧长为多少?
n°的圆心角所对的弧长为多少?
试一试
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为: l =________。
例题赏析
驶向胜利的彼岸
求弧长,你会了吗?
练一练
驶向胜利的彼岸
探索面积公式
设一圆的为⊙O,半径为r。
圆面积为多少?
圆周角为360°,则1°的圆心角所对的扇形面积为多少?
n°的圆心角所对的扇形面积为多少?
试一试
如果扇形的半径为R,圆心角为n°,那么扇形的面积的计算公式为: S扇=______。
R
试一试
例1:
扇形AOB的半径为30cm,∠AOB=120°,
1、求弧AB的长(结果精确到0.1cm)
2、扇形AOB的面积(结果精确到0.1cm2)
例题赏析
例题赏析
n°
l
O
比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?
探索弧长与扇形面积的关系
S
r
探索发现
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?
跟踪训练
挑战自我
练习1:扇形的面积是S,它的半径是r,求这个扇形的弧长.
练习2:如图,在同心圆中,两圆半径分别为2, 1,∠AOB=120°,求阴影部分的面积.
A
B
O
120°
练一练
B
C
A
⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少?
挑战极限
B
C
A
D
⊙A, ⊙B, ⊙C, ⊙D两两不相交,且半径都是1cm,则图中的四个扇形的面积之和为多少?弧长的和为多少?
挑战极限
⊙A, ⊙B, ⊙C, ⊙D ,⊙E两两不相交,且半径都是1cm,则图中的五个扇形的面积之和为多少?弧长的和为多少?
B
C
A
D
E
若象这样的n个圆呢?
挑战极限
挑战自我
习题4.7 3-2题
祝你成功!
独立作业
驶向胜利的彼岸
结束寄语
形成天才的决定因素应该是勤奋.
下课了!
再见
补充:
如图,某传送带的一个转动轮的半径为10cm.
1)转动轮转一周,传送带上的物品A被传送多少厘米?
2)转动轮转1°,传送带上的物品A被传送多少厘米?
3)转动轮转n°,传送带上的物品A被传送多少厘米?
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
