2021-2022学年八年级数学人教版上册11.3.2多边形的内角和 课件(共31张PPT)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册11.3.2多边形的内角和 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 912.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览




文档简介
(共31张PPT)
多边形的内角和
生活中的多边形
你知道下列图形有那些几何图形
三角形
四边形
五边形
六边形
八边形
四边形
三角形的内角和等于
.正方形、长
方形的内角和都等于
.
?
思考
其他四边形的内角和等于多少?
180°
360°
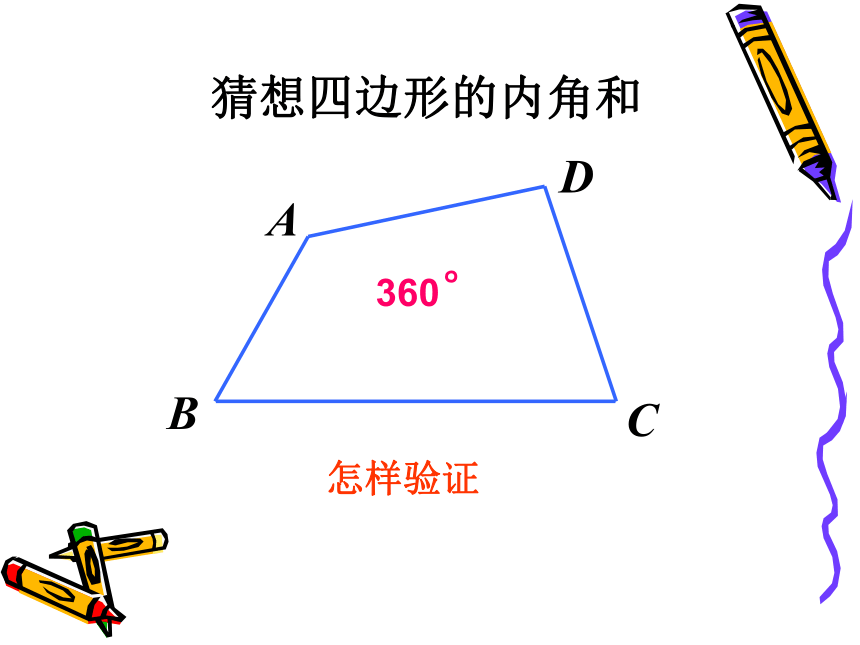
猜想四边形的内角和
A
D
C
B
怎样验证
360°
探究四边形的内角和
A
D
C
B
量
拼
分
3.量一量:你画的多边形每个内角是多少度
动手画一画
1.
请同学们在笔记本上画一个多边形
2.
给你画的多边形的每个端点标上字母
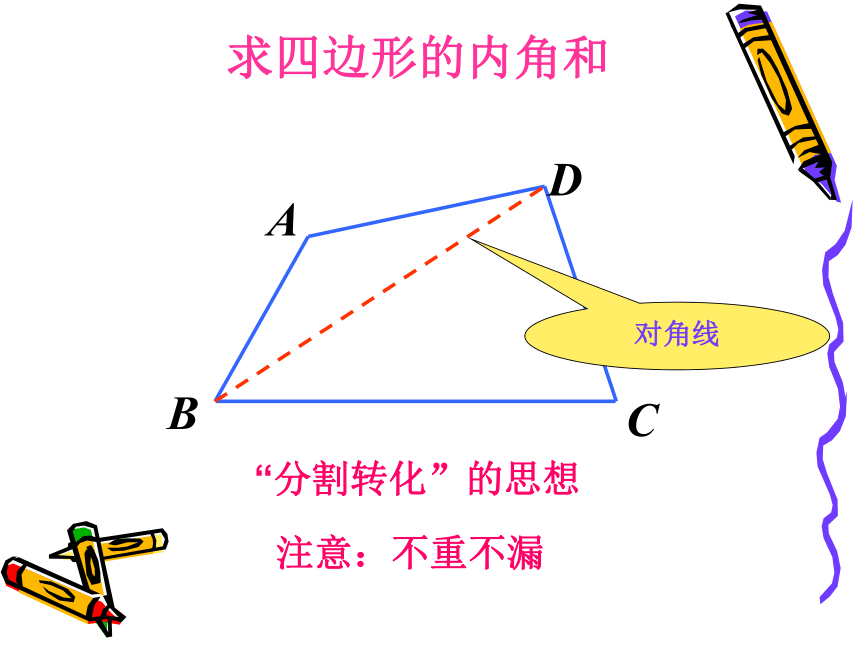
求四边形的内角和
A
D
C
B
对角线
“分割转化”的思想
注意:不重不漏
探究
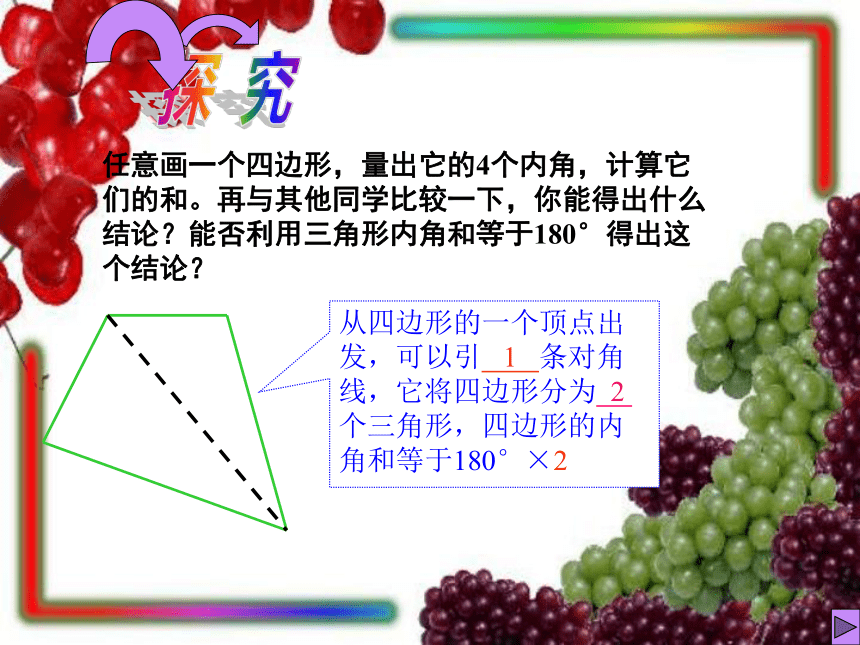
任意画一个四边形,量出它的4个内角,计算它们的和。再与其他同学比较一下,你能得出什么结论?能否利用三角形内角和等于180°得出这个结论?
从四边形的一个顶点出发,可以引
1
条对角线,它将四边形分为
2
个三角形,四边形的内角和等于180°×2
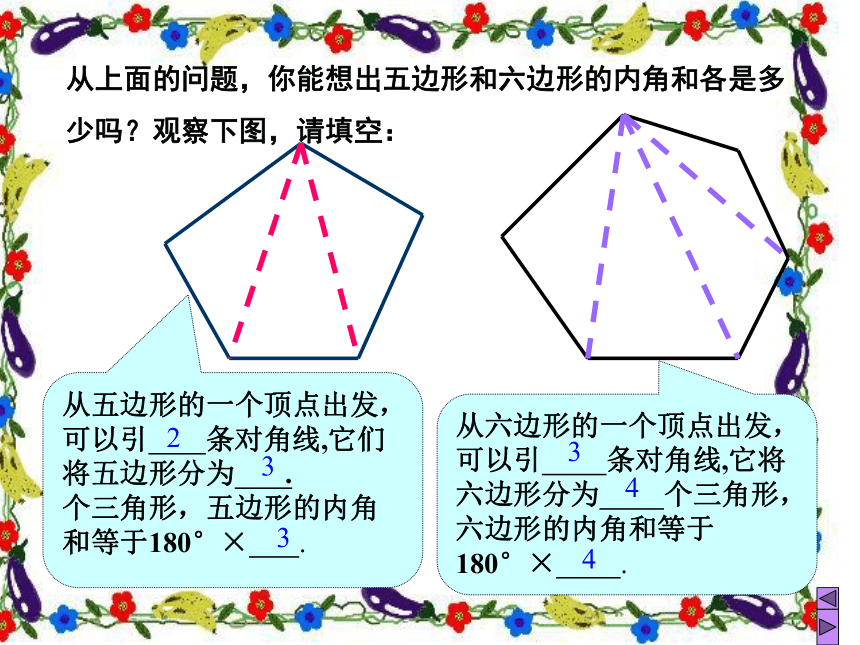
从上面的问题,你能想出五边形和六边形的内角和各是多
少吗?观察下图,请填空:
从五边形的一个顶点出发,可以引
条对角线,它们将五边形分为
.
个三角形,五边形的内角和等于180°×
.
从六边形的一个顶点出发,可以引
条对角线,它将六边形分为
个三角形,六边形的内角和等于180°×
.
2
3
3
3
4
4
多边形的对角线:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
如图中的虚线表示的线段就是所画的多边形的对角线.
n边形
对角线条数
4
5
6
2
5
9
n
3
0
一般地,怎样求n边形的内角和呢?
请观察图形填空:
友情提醒
画多边形时,倒数第二边应画成虚线,表示还有很多边未画出来
A1
A2
A3
A4
A5
An
从n边形的一个顶点出发,可以引
条对角线,它们将n边形分为
个三角形,n边形的内角和等于180°×
.
(n-3)
(n-2)
(n-2)
A
C
B
如图,三角形ABC的内角和是多少度?
探索多边形的内角和
探索多边形的内角和
A
B
C
D
四边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
E
五边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
F
E
六边形的内角和是多少度?
图中有几个三角形?
探究多边形的内角和
:填写下表
多边形
多边形
的边数
从一个顶点
引对角线
的条数
分成三角
形的个数
多边形的
内角和
4
1
2
2×180°
5
2
3
3×180°
6
3
4
4×180°
n
n-3
4-3=
5-3=
6-3=
n-2
4-2=
5-2=
6-2=
(n-2)×180°
n边形的内角和=(n-2)×
180°
(n≥3)
我终于证明了本节课的结论啦
议一议:
把一个多边形分成几个三角形,还有其它分法吗?由新的分法,能得出多边形内角和公式吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180
°,但每个图中都有一个以红圈圈住的点,它是一个圆周角360
°,因此n边形的内角和为
n×180
°-
360
°=
(n-2)×180
°
多了什么?如何处理?
·
·
n边形的内角和为
n边形的内角和为
n×180°
即
(n-2)
×180°.
(n-1)
×180°
即
(n-2)
×180°.
探索:多边形的内角和
-
360°
-180°
探索多边形的内角和关键是:
把多边形分成几个三角形,再利用三角形的内角和求得。
议
一
议
你还有其它的分法吗?
P
A
E
D
C
B
A
E
D
C
B
P
n×180o-360o
(n-1)×180o-180o
课后探索
1、n边形从一个顶点所画对角线的条数是
;分三角形个数是
;
2、n边形内角和
=
;
3、九边形的内角和是__________;
4、一个多边形的内角和为1620度,求边数
;
5
、
一个四边形有两个内角和为180度,则另两个内角和为
,其关系是
。
课
堂
测
试
n-3
(
n
-
2
)×
180
°
1260°
11
180°
互补
n-3
例1
求八边形的内角和是
解:多边形内角和为(n-2)×180°
八边形的内角和为(8-2)×180°=1080°
1080°
例2
一个多边形的内角和为1440°,
求边数n=
解:多边形内角和为(n-2)×180°
该多边形的内角和为1440°,则:
(n-2)×180°
=1440°
n=10
10
今天的收获
3、n边形的内角和等于:(n-2)×180°
2、n边形从一个顶点所画对角线的条数为:
n-3所分得三角形的个数为
:
n-2
??
4、利用“分割转化”的学习方法,可以把多边形问题转化为三角形问题来解决
1、连接多边形不相邻的两个顶点的线段叫做多边形对对角线
课后作业
1、已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形的边数为
;
2、一个多边形的边数增加1,则内角和增加的度数是(??
?
);
A.60°???????
B.90°??????
C.180°??
??D.360°
6
C
3
、
求下列图形中
x的值
140°
x°
x°
90°
2x
°
150
°
120
°
x
°
X°
80
°
75
°
120
°
60
°
135
°
E
B
C
D
150
°
A
X
°
90°
2x
°
150
°
120
°
x
°
90°
2x
°
150
°
120
°
x
°
90°
2x
°
150
°
120
°
x
°
65
60
95
120
75
AB//CD
120
板书设计
7.3.2
多边形的内角和
A
B
C
D
三角形的内角和是180°
四边形的内角和是
(4-2)·180°
n边形的内角和是(n-2)·180°
本节课你收获了什么?
小结:
多边形的内角和
生活中的多边形
你知道下列图形有那些几何图形
三角形
四边形
五边形
六边形
八边形
四边形
三角形的内角和等于
.正方形、长
方形的内角和都等于
.
?
思考
其他四边形的内角和等于多少?
180°
360°
猜想四边形的内角和
A
D
C
B
怎样验证
360°
探究四边形的内角和
A
D
C
B
量
拼
分
3.量一量:你画的多边形每个内角是多少度
动手画一画
1.
请同学们在笔记本上画一个多边形
2.
给你画的多边形的每个端点标上字母
求四边形的内角和
A
D
C
B
对角线
“分割转化”的思想
注意:不重不漏
探究
任意画一个四边形,量出它的4个内角,计算它们的和。再与其他同学比较一下,你能得出什么结论?能否利用三角形内角和等于180°得出这个结论?
从四边形的一个顶点出发,可以引
1
条对角线,它将四边形分为
2
个三角形,四边形的内角和等于180°×2
从上面的问题,你能想出五边形和六边形的内角和各是多
少吗?观察下图,请填空:
从五边形的一个顶点出发,可以引
条对角线,它们将五边形分为
.
个三角形,五边形的内角和等于180°×
.
从六边形的一个顶点出发,可以引
条对角线,它将六边形分为
个三角形,六边形的内角和等于180°×
.
2
3
3
3
4
4
多边形的对角线:
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
如图中的虚线表示的线段就是所画的多边形的对角线.
n边形
对角线条数
4
5
6
2
5
9
n
3
0
一般地,怎样求n边形的内角和呢?
请观察图形填空:
友情提醒
画多边形时,倒数第二边应画成虚线,表示还有很多边未画出来
A1
A2
A3
A4
A5
An
从n边形的一个顶点出发,可以引
条对角线,它们将n边形分为
个三角形,n边形的内角和等于180°×
.
(n-3)
(n-2)
(n-2)
A
C
B
如图,三角形ABC的内角和是多少度?
探索多边形的内角和
探索多边形的内角和
A
B
C
D
四边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
E
五边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
F
E
六边形的内角和是多少度?
图中有几个三角形?
探究多边形的内角和
:填写下表
多边形
多边形
的边数
从一个顶点
引对角线
的条数
分成三角
形的个数
多边形的
内角和
4
1
2
2×180°
5
2
3
3×180°
6
3
4
4×180°
n
n-3
4-3=
5-3=
6-3=
n-2
4-2=
5-2=
6-2=
(n-2)×180°
n边形的内角和=(n-2)×
180°
(n≥3)
我终于证明了本节课的结论啦
议一议:
把一个多边形分成几个三角形,还有其它分法吗?由新的分法,能得出多边形内角和公式吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180
°,但每个图中都有一个以红圈圈住的点,它是一个圆周角360
°,因此n边形的内角和为
n×180
°-
360
°=
(n-2)×180
°
多了什么?如何处理?
·
·
n边形的内角和为
n边形的内角和为
n×180°
即
(n-2)
×180°.
(n-1)
×180°
即
(n-2)
×180°.
探索:多边形的内角和
-
360°
-180°
探索多边形的内角和关键是:
把多边形分成几个三角形,再利用三角形的内角和求得。
议
一
议
你还有其它的分法吗?
P
A
E
D
C
B
A
E
D
C
B
P
n×180o-360o
(n-1)×180o-180o
课后探索
1、n边形从一个顶点所画对角线的条数是
;分三角形个数是
;
2、n边形内角和
=
;
3、九边形的内角和是__________;
4、一个多边形的内角和为1620度,求边数
;
5
、
一个四边形有两个内角和为180度,则另两个内角和为
,其关系是
。
课
堂
测
试
n-3
(
n
-
2
)×
180
°
1260°
11
180°
互补
n-3
例1
求八边形的内角和是
解:多边形内角和为(n-2)×180°
八边形的内角和为(8-2)×180°=1080°
1080°
例2
一个多边形的内角和为1440°,
求边数n=
解:多边形内角和为(n-2)×180°
该多边形的内角和为1440°,则:
(n-2)×180°
=1440°
n=10
10
今天的收获
3、n边形的内角和等于:(n-2)×180°
2、n边形从一个顶点所画对角线的条数为:
n-3所分得三角形的个数为
:
n-2
??
4、利用“分割转化”的学习方法,可以把多边形问题转化为三角形问题来解决
1、连接多边形不相邻的两个顶点的线段叫做多边形对对角线
课后作业
1、已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形的边数为
;
2、一个多边形的边数增加1,则内角和增加的度数是(??
?
);
A.60°???????
B.90°??????
C.180°??
??D.360°
6
C
3
、
求下列图形中
x的值
140°
x°
x°
90°
2x
°
150
°
120
°
x
°
X°
80
°
75
°
120
°
60
°
135
°
E
B
C
D
150
°
A
X
°
90°
2x
°
150
°
120
°
x
°
90°
2x
°
150
°
120
°
x
°
90°
2x
°
150
°
120
°
x
°
65
60
95
120
75
AB//CD
120
板书设计
7.3.2
多边形的内角和
A
B
C
D
三角形的内角和是180°
四边形的内角和是
(4-2)·180°
n边形的内角和是(n-2)·180°
本节课你收获了什么?
小结:
