2021-2022学年冀教版数学九年级上册《23.4 用样本估计总体》课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年冀教版数学九年级上册《23.4 用样本估计总体》课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 481.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 07:09:46 | ||
图片预览






文档简介
(共21张PPT)
23.4
用样本估计总体
第二十三章
数据分析
导入新课
讲授新课
当堂练习
课堂小结
情境引入
1.回顾平均数的知识,能够用样本平均数估计总体平均数.
2.学会用样本方差估计总体方差.
(重点、难点)
学习目标
问题1
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+
…+fk=n),那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的
.其中f1,f2,…,fk分别叫做x1,x2,…,xk的权
导入新课
问题与思考
加权平均数
问题2
方差的计算公式:
_____________,
方差越大,__
______越大;方差越小,___________
越小.
数据的波动
数据的波动
问题1
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少(结果取整数)?
讲授新课
样本平均数估计总体平均数
一
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
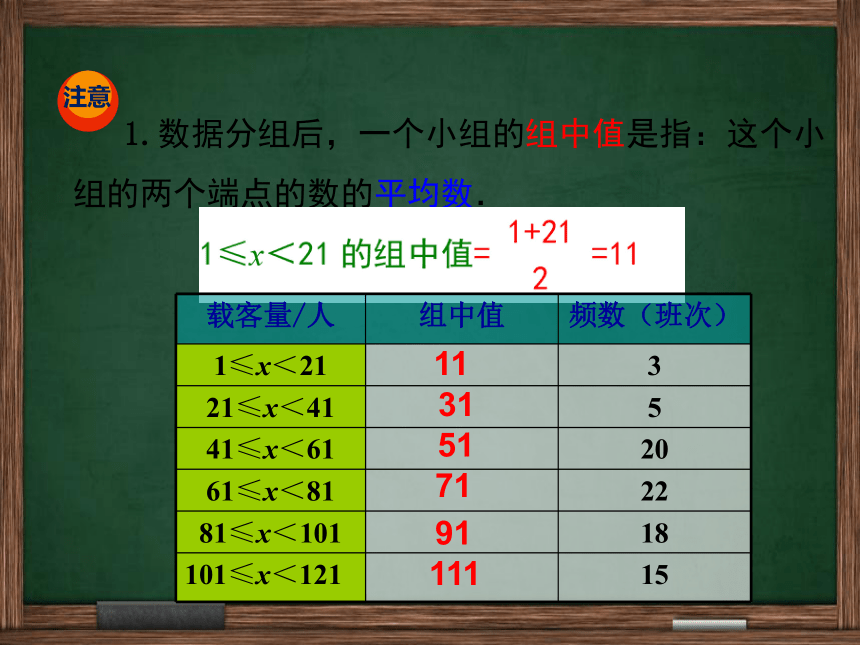
注意
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
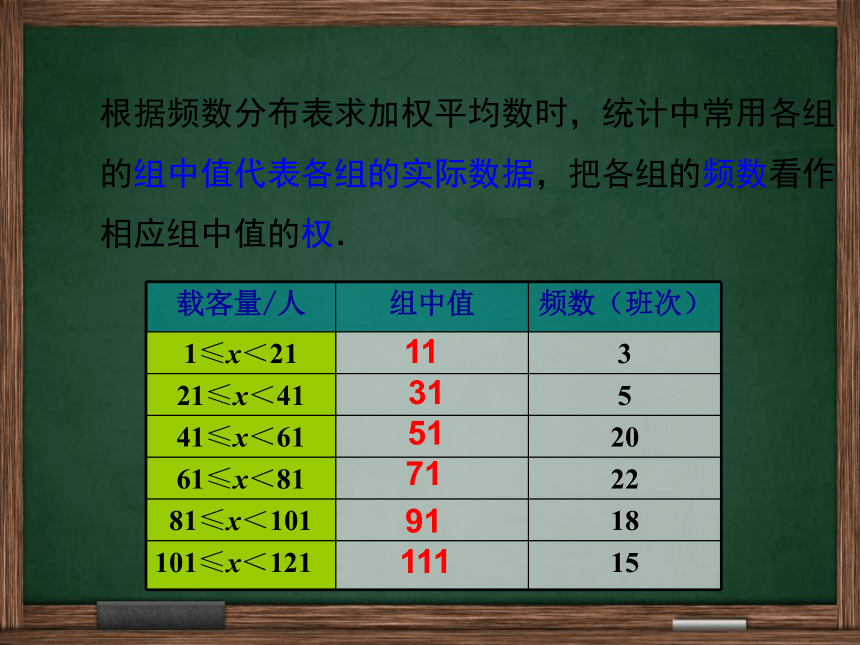
根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
解:这天5路公共汽车平均每班的载客量是:
我们知道,当要考察的对象很多或考察本身带有破坏性时,统计学中常常使用样本数据的代表意义估计总体的方法来获得对总体的认识.
例如,实际生活中经常用样本的平均数来估计总体的平均数.
归纳
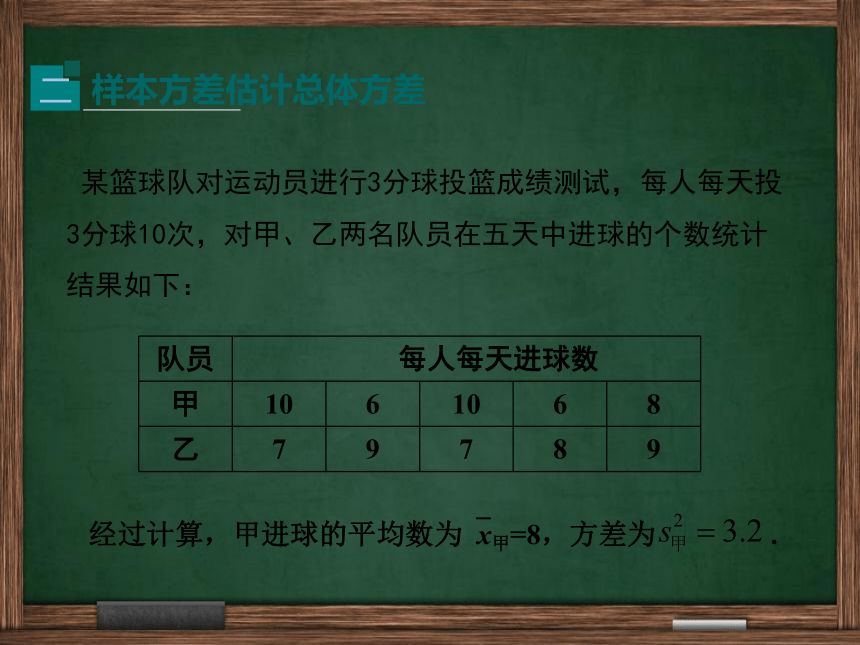
某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
样本方差估计总体方差
二
队员
每人每天进球数
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为?x甲=8,方差为
.
问题1
乙进球的平均数和方差是多少?
问题2
现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.
方差越大,数据的波动越大;方差越小,数据
的波动越小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数
相等或相近时,再利用样本方差来估计总体数据的
波动情况.
归纳
例1:某农民几年前承包了甲、乙两片荒山,各栽了100棵蜜橘,成活98%,现已挂果,经济效益显著,为了分析经营情况,他从甲山随意采摘了3棵树上的蜜橘称得质量分别为25,18,20、21千克;他从乙山随意采摘了4棵树上的蜜橘,称得质量分别为21,24,19,20千克.如下表:
典例精析
甲(千克)
25
18
20
21
乙(千克)
21
24
19
20
(1)样本容量是多少?
(1)4+4=8;
解:
甲(千克)
25
18
20
21
乙(千克)
21
24
19
20
(2)样本平均数是多少?并估算出甲、乙两山蜜橘
的总产量?
解:x甲=21,
?x乙=21
(3)甲、乙两山哪个山上蜜橘长势较整齐?
甲(千克)
25
18
20
21
乙(千克)
21
24
19
20
__
例2:某校为了解八年级男生的身高,从八年级各班随机抽查了共40名男同学,测量身高情况(单位:cm)图.试估计该校八年级全部男生的平均身高.
身高/cm
提示
由频数分布直方图可知:各组的组中值依次是:
150cm,160cm,170cm,180cm.各组的频数依次是6人,10人,20人,4人,计算出样本的平均身高.
5
10
15
20
0
145
155
165
175
185
6
10
20
4
人数
样本估计总体
解:由频数分布直方图可知:各组的组中值依次是:150cm,160cm,170cm,180cm.各组的频数依次是6人,10人,20人,4人,计算出样本的平均身高.
所以可估计该校八年级全部男生的平均身高是165.5cm.
当堂练习
果园里有100
棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
(1)果农从100
棵梨树中任意选出10
棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
所以,平均每棵梨树上梨的个数为154.
12
梨的质量
x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
16
8
(2)果农从这10
棵梨树的每一棵树上分别随机摘4
个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以,平均每个梨的质量约为0.42
kg.
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
思考 这个生活中的问题是如何解决的,体现了怎样的统计思想?
所以,该果园中梨的总产量约为6468kg.
课堂小结
2.在抽样调查得到样本数据后,你如何处理样本数据并估计总体数据的集中趋势?
样本平均数估计总体平均数.
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
用样本估计总体是统计的基本思想,正如用样本平均数估计总体平均数一样,考察总体方差时,如果所要考察的总体包含很多个体,或者考察本身带有破坏性,实际常常用样本的方差来估计总体的方差.
3.在什么情况下要用样本的方差估计总体方差?
4.用样本的方差估总体方差要注意什么?
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
23.4
用样本估计总体
第二十三章
数据分析
导入新课
讲授新课
当堂练习
课堂小结
情境引入
1.回顾平均数的知识,能够用样本平均数估计总体平均数.
2.学会用样本方差估计总体方差.
(重点、难点)
学习目标
问题1
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+
…+fk=n),那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的
.其中f1,f2,…,fk分别叫做x1,x2,…,xk的权
导入新课
问题与思考
加权平均数
问题2
方差的计算公式:
_____________,
方差越大,__
______越大;方差越小,___________
越小.
数据的波动
数据的波动
问题1
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少(结果取整数)?
讲授新课
样本平均数估计总体平均数
一
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
注意
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
解:这天5路公共汽车平均每班的载客量是:
我们知道,当要考察的对象很多或考察本身带有破坏性时,统计学中常常使用样本数据的代表意义估计总体的方法来获得对总体的认识.
例如,实际生活中经常用样本的平均数来估计总体的平均数.
归纳
某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
样本方差估计总体方差
二
队员
每人每天进球数
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为?x甲=8,方差为
.
问题1
乙进球的平均数和方差是多少?
问题2
现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
(1)在解决实际问题时,方差的作用是什么?
反映数据的波动大小.
方差越大,数据的波动越大;方差越小,数据
的波动越小,可用样本方差估计总体方差.
(2)运用方差解决实际问题的一般步骤是怎样的?
先计算样本数据平均数,当两组数据的平均数
相等或相近时,再利用样本方差来估计总体数据的
波动情况.
归纳
例1:某农民几年前承包了甲、乙两片荒山,各栽了100棵蜜橘,成活98%,现已挂果,经济效益显著,为了分析经营情况,他从甲山随意采摘了3棵树上的蜜橘称得质量分别为25,18,20、21千克;他从乙山随意采摘了4棵树上的蜜橘,称得质量分别为21,24,19,20千克.如下表:
典例精析
甲(千克)
25
18
20
21
乙(千克)
21
24
19
20
(1)样本容量是多少?
(1)4+4=8;
解:
甲(千克)
25
18
20
21
乙(千克)
21
24
19
20
(2)样本平均数是多少?并估算出甲、乙两山蜜橘
的总产量?
解:x甲=21,
?x乙=21
(3)甲、乙两山哪个山上蜜橘长势较整齐?
甲(千克)
25
18
20
21
乙(千克)
21
24
19
20
__
例2:某校为了解八年级男生的身高,从八年级各班随机抽查了共40名男同学,测量身高情况(单位:cm)图.试估计该校八年级全部男生的平均身高.
身高/cm
提示
由频数分布直方图可知:各组的组中值依次是:
150cm,160cm,170cm,180cm.各组的频数依次是6人,10人,20人,4人,计算出样本的平均身高.
5
10
15
20
0
145
155
165
175
185
6
10
20
4
人数
样本估计总体
解:由频数分布直方图可知:各组的组中值依次是:150cm,160cm,170cm,180cm.各组的频数依次是6人,10人,20人,4人,计算出样本的平均身高.
所以可估计该校八年级全部男生的平均身高是165.5cm.
当堂练习
果园里有100
棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
(1)果农从100
棵梨树中任意选出10
棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
所以,平均每棵梨树上梨的个数为154.
12
梨的质量
x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
16
8
(2)果农从这10
棵梨树的每一棵树上分别随机摘4
个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以,平均每个梨的质量约为0.42
kg.
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
思考 这个生活中的问题是如何解决的,体现了怎样的统计思想?
所以,该果园中梨的总产量约为6468kg.
课堂小结
2.在抽样调查得到样本数据后,你如何处理样本数据并估计总体数据的集中趋势?
样本平均数估计总体平均数.
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
用样本估计总体是统计的基本思想,正如用样本平均数估计总体平均数一样,考察总体方差时,如果所要考察的总体包含很多个体,或者考察本身带有破坏性,实际常常用样本的方差来估计总体的方差.
3.在什么情况下要用样本的方差估计总体方差?
4.用样本的方差估总体方差要注意什么?
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
