2021—2022学年人教版数学八年级上册_11.2. 1 三角形的内角和 课件(共30张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册_11.2. 1 三角形的内角和 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 940.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 07:35:49 | ||
图片预览







文档简介
(共30张PPT)
11.2
与三角形有关的角
教学目标
导入新课
如图,小明同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是把哪块玻璃块带去。
3号
教学目标
新课讲解
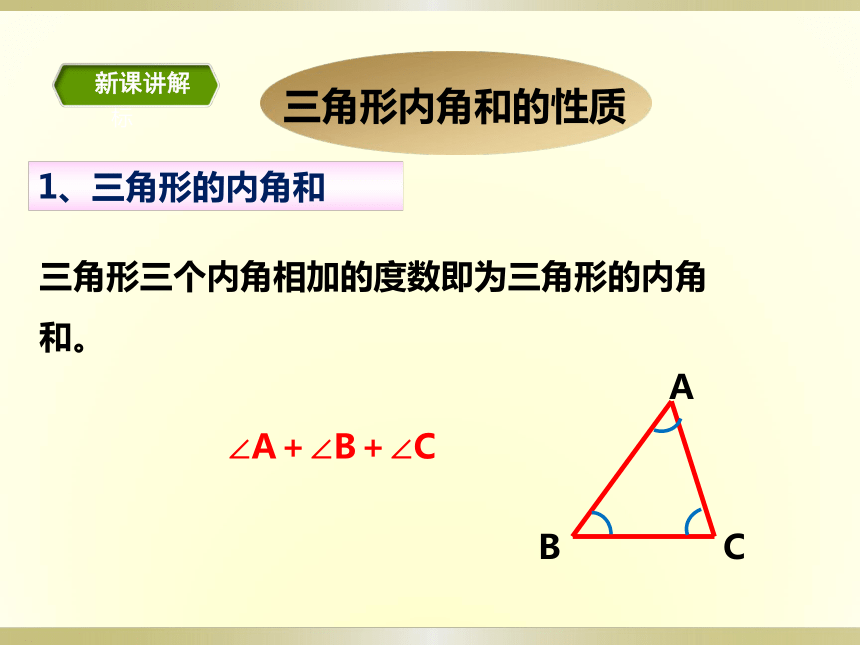
三角形内角和的性质
三角形三个内角相加的度数即为三角形的内角和。
1、三角形的内角和
A
B
C
∠A+∠B+∠C
想一想
三角形的三个内角和是多少?
180°
方法一:
度量法
通过具体的度量,验证三角形的内角和为180°.
你有什么办法可以验证呢?
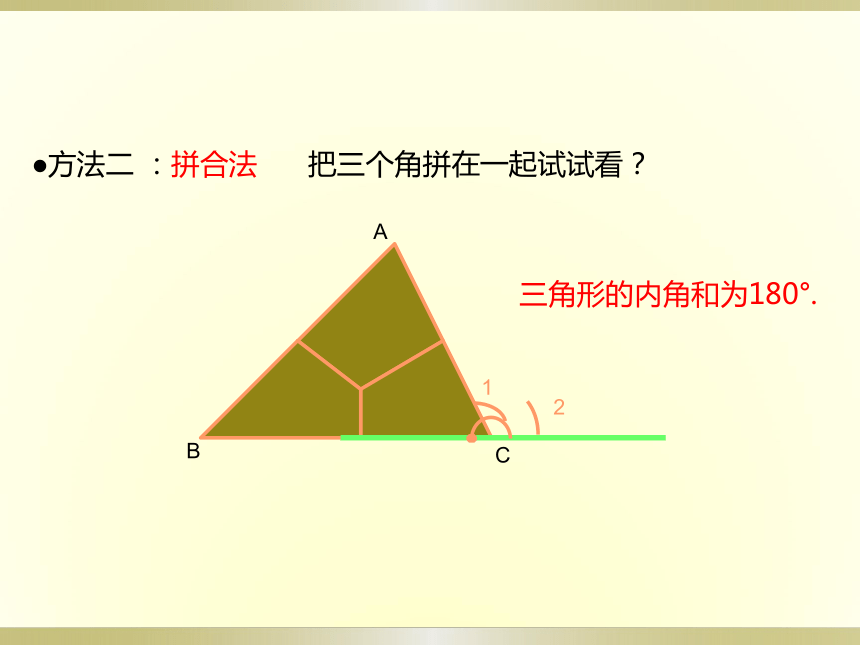
方法二
:拼合法
把三个角拼在一起试试看?
A
B
C
2
1
三角形的内角和为180°.
问题:有什么方法可以得到180
°
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
从刚才拼角的过程你能想出证明的方法吗?
3、邻补角的和是180
°
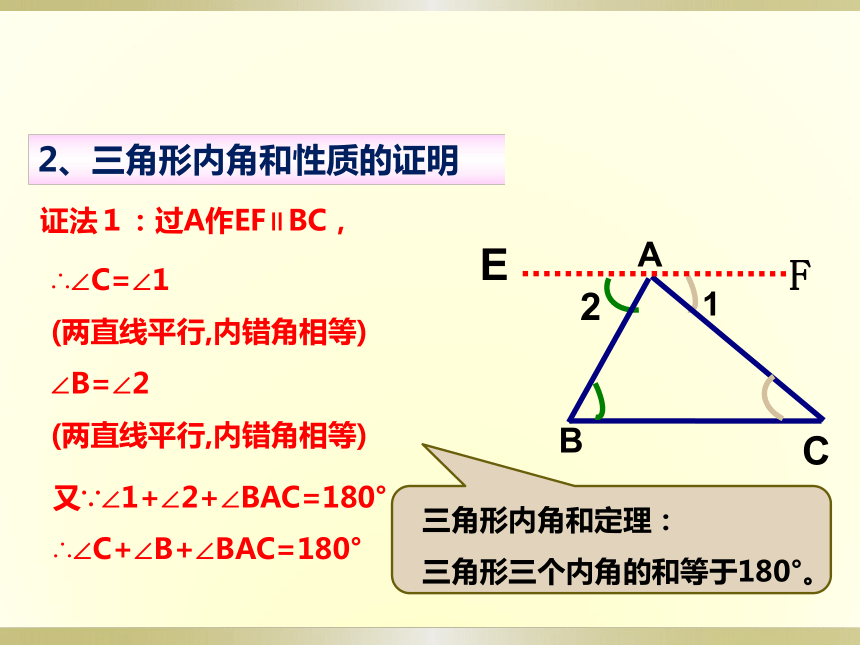
证法1:过A作EF∥BC,
F
2
1
E
C
B
A
2、三角形内角和性质的证明
∴∠C=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,内错角相等)
又∵∠1+∠2+∠BAC=180°
∴∠C+∠B+∠BAC=180°
三角形内角和定理:
三角形三个内角的和等于180°。
证法2:过A作AE∥BC,
F
1
E
C
B
A
∴∠B=∠1
,
(两直线平行,内错角相等)
∠1+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
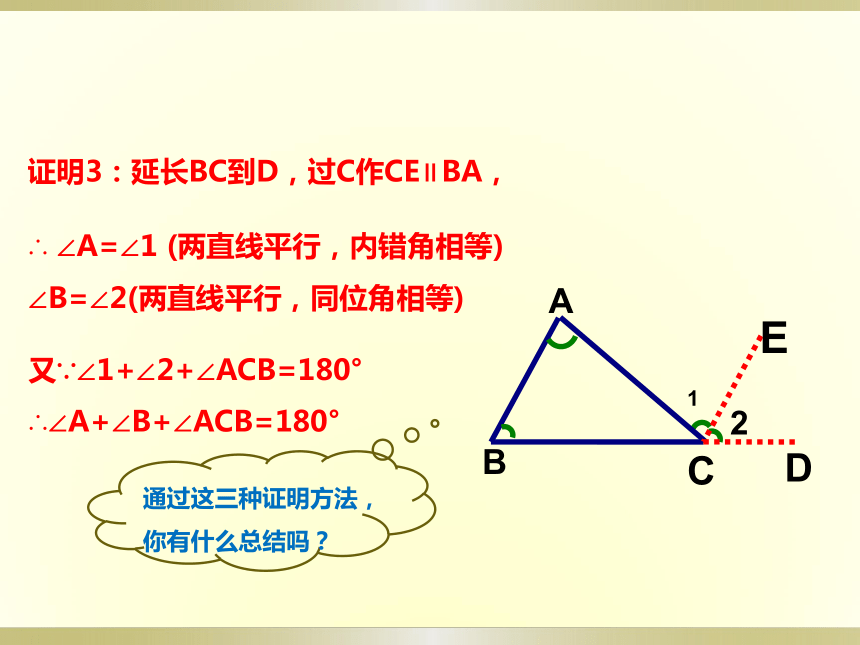
证明3:延长BC到D,过C作CE∥BA,
2
1
E
D
C
B
A
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
通过这三种证明方法,你有什么总结吗?
在这里,为了证明的需要,在原来的图形上添加的线叫做辅助线。
为了证明三个角的和为180°,转化为一个平角或同旁内角,这种转化思想是数学中的常用方法。
在平面几何里,辅助线通常画成虚线。
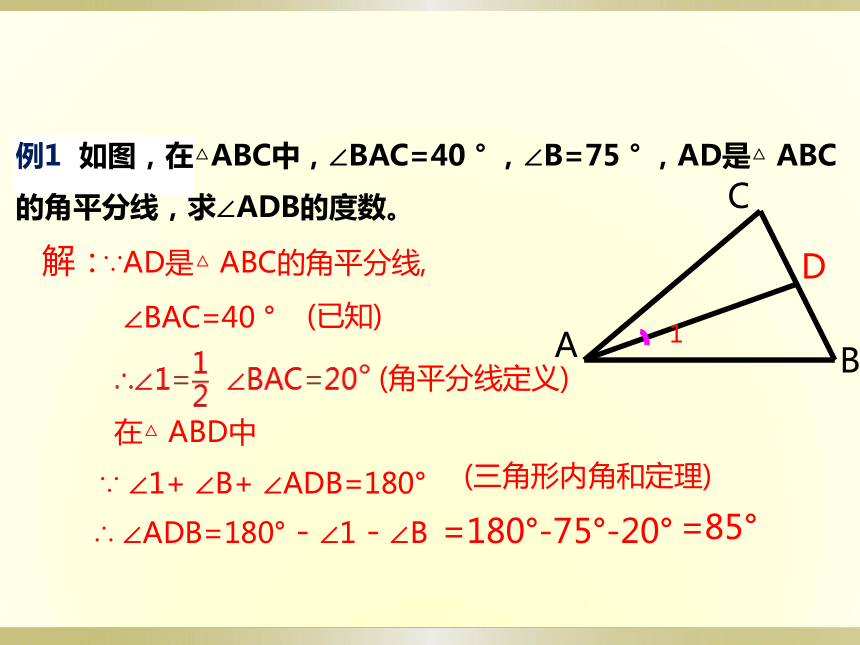
例1
如图,在△ABC中,∠BAC=40
°
,∠B=75
°
,AD是△
ABC的角平分线,求∠ADB的度数。
C
D
B
A
解:
∵AD是△
ABC的角平分线,
∠BAC=40
°
1
(已知)
∴∠1=
∠BAC=20°
(角平分线定义)
在△
ABD中
∵
∠1+
∠B+
∠ADB=180°
(三角形内角和定理)
∴
∠ADB=180°-∠1-∠B
=180°-75°-20°
=85°
教学目标
牛刀小试
(1)在△ABC中,∠A=35°,∠
B=43
°
则∠
C=
。
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4
则∠A
=
∠
B=
∠
C=
。
102°
80°
60°
40°
(3)在△ABC中,
∠A=40
°
∠A=2∠B,则∠C=
。
120°
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向。从C岛看A、B两岛的视角∠ACB是多少度?
解:∠CAB=
∠BAD
-
∠CAD
=80°-50°=
30°
∵AD∥BE,得:
∠BAD
+∠BADE=180°
∴
∠ABE=180°-
∠BAD
=
180°-
80°=100°
∠ABC=∠ABE-∠EBC=
100°-
40°=60°
在△ABC中
,∠ACB=
180°-
∠ABC
-∠CAB
=
180°-
60°-
30°=
90°
答:从B岛看A,C两岛的视角∠ABC是60°,从C岛看A、B两岛的视角∠ACB是90°
你能找出上图中所包含的直角三角形吗
?
3、直角三角形的内角和
直角三角形的两锐角互余.
在Rt△ABC中.
∵∠A+∠B
+∠C
=
180°,(三角形内角和定理)
而∠C
=
90°,
∴
∠A+∠B
=
90°.
三角形用什么符号表示的?那么直
角三角形又用什么符号表示呢?
三角形ABC表示为:
直角三角形可以用符号:
如图直角三角形ABC表示为:
△ABC
Rt△
Rt△ABC
例3:如图,∠C
=∠D
=90°,AD,BC
相交于点E,
∠CAE
与∠DBE
有什么关系?
C
D
E
A
B
∠CAE
=∠DBE
解:在Rt△ACE中,∠CAE=90°-∠AEC.
在Rt△ACE中,∠DBE=90°-∠BED
∵
∠AEC=∠BED
∴
∠CAE
=∠DBE
想一想:如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?请说明理由.
已知:(如图)在△ABC中,
∠A+∠B
=
90°.
求证:△ABC是直角三角形.
证明:在△ABC中,
∠A+∠B+∠C
=?180°,(三角形内角和定理)
∵?∠A+∠B
=
90°,(已知)
∴?∠C
=
90°,
∴?△ABC是直角三角形.(直角三角形定义)
结论:有两个角互余的三角形是直角三角形.
教学目标
牛刀小试
如果一个三角形的两个内角分别是36°和54°,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
解析:第三个角是180°-36°-54°=90°,
∴三角形是直角三角形.
故选B.
不需要计算,你能得到答案吗?
B
教学目标
巩固提升
解析:设∠A=x°,则∠ABC=∠C=2x°,根据三角形内角和性质可知x+2x+2x=18°
解得x=36
∴∠C=2×36°=72°
在△BDC中,∵
BD是AC边上的高
∴∠BDC=90°;∴∠DBC=90°-72°;∴∠DBC=18°
1.已知△ABC中,∠ABC=∠C=2∠A
,BD是AC边上的高,求∠DBC的度数。
18°
解析:设此三角形的三个内角分别为x°、2x°、x°
则由三角形的内角和性质可知:x°+2x°+x°=180°。∴x=45°
则此三角形的三个内角分别为45°、90°、45°。
故答案选D。
2.一个三角形的三个内角的度数比是1:2:1,这个三角形是(
)?
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
D
解析:设∠A为x,则∠B=2∠A=2x,∠C=3∠A=3x
∵三角形的内角和为180°
∴x+2x+3x=180°,∴x=30°
则此三角形的三个内角为30°、60°、90°,故此三角形为直角三角形。
3.
在△ABC中,如果∠A=∠B=∠C,那么△ABC是什么三角形?
直角三角形
4.如图,△ABC中,∠ABC和∠ACB的平分线交于点O.
(1)
若∠ABC=60°,∠ACB=80°,求∠BOC的度数。
(2)
若∠A=70°,
求∠BOC的度数。
解:(1)∵∠ABC和∠ACB的平分线交于点O,
∠ABC=60°,∠ACB=80°
∴∠OBC=∠ABC=×60°=30°
∠OCB=∠ACB=×80°=40°
∵∠BOC+∠OCB+∠OBC=180°
∴∠BOC=180°-40°-30°=110°
(2)∵∠ABC和∠ACB的平分线交于点O,∴∠OBC=∠ABC,∠OCB=∠ACB
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)
∵∠A=70°∴∠ABC+∠ACB
=180°-∠A=180°-70°=110°
∴∠OBC+∠OCB=×110°=55°
∵∠BOC+∠OCB+∠OBC=180°
∴∠BOC=180°-55°=125°
5.如图,甲楼楼高16米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为45°,此时,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应当是多少米?
解:由题意可知:
∠ABC=90°,∠ACB=45°
∴∠BAC=180°-∠ABC-∠ACB
=180°-90°-45°
=45°
∴BC=AB=16米
答:两楼的距离是16米。
教学目标
课堂小结
1、三角形的内角和
2、三角形内角和性质
3、三角形的判断
11.2
与三角形有关的角
教学目标
导入新课
如图,小明同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是把哪块玻璃块带去。
3号
教学目标
新课讲解
三角形内角和的性质
三角形三个内角相加的度数即为三角形的内角和。
1、三角形的内角和
A
B
C
∠A+∠B+∠C
想一想
三角形的三个内角和是多少?
180°
方法一:
度量法
通过具体的度量,验证三角形的内角和为180°.
你有什么办法可以验证呢?
方法二
:拼合法
把三个角拼在一起试试看?
A
B
C
2
1
三角形的内角和为180°.
问题:有什么方法可以得到180
°
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
从刚才拼角的过程你能想出证明的方法吗?
3、邻补角的和是180
°
证法1:过A作EF∥BC,
F
2
1
E
C
B
A
2、三角形内角和性质的证明
∴∠C=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,内错角相等)
又∵∠1+∠2+∠BAC=180°
∴∠C+∠B+∠BAC=180°
三角形内角和定理:
三角形三个内角的和等于180°。
证法2:过A作AE∥BC,
F
1
E
C
B
A
∴∠B=∠1
,
(两直线平行,内错角相等)
∠1+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
证明3:延长BC到D,过C作CE∥BA,
2
1
E
D
C
B
A
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
通过这三种证明方法,你有什么总结吗?
在这里,为了证明的需要,在原来的图形上添加的线叫做辅助线。
为了证明三个角的和为180°,转化为一个平角或同旁内角,这种转化思想是数学中的常用方法。
在平面几何里,辅助线通常画成虚线。
例1
如图,在△ABC中,∠BAC=40
°
,∠B=75
°
,AD是△
ABC的角平分线,求∠ADB的度数。
C
D
B
A
解:
∵AD是△
ABC的角平分线,
∠BAC=40
°
1
(已知)
∴∠1=
∠BAC=20°
(角平分线定义)
在△
ABD中
∵
∠1+
∠B+
∠ADB=180°
(三角形内角和定理)
∴
∠ADB=180°-∠1-∠B
=180°-75°-20°
=85°
教学目标
牛刀小试
(1)在△ABC中,∠A=35°,∠
B=43
°
则∠
C=
。
(2)在△ABC中,
∠A
:∠B:∠C=2:3:4
则∠A
=
∠
B=
∠
C=
。
102°
80°
60°
40°
(3)在△ABC中,
∠A=40
°
∠A=2∠B,则∠C=
。
120°
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向。从C岛看A、B两岛的视角∠ACB是多少度?
解:∠CAB=
∠BAD
-
∠CAD
=80°-50°=
30°
∵AD∥BE,得:
∠BAD
+∠BADE=180°
∴
∠ABE=180°-
∠BAD
=
180°-
80°=100°
∠ABC=∠ABE-∠EBC=
100°-
40°=60°
在△ABC中
,∠ACB=
180°-
∠ABC
-∠CAB
=
180°-
60°-
30°=
90°
答:从B岛看A,C两岛的视角∠ABC是60°,从C岛看A、B两岛的视角∠ACB是90°
你能找出上图中所包含的直角三角形吗
?
3、直角三角形的内角和
直角三角形的两锐角互余.
在Rt△ABC中.
∵∠A+∠B
+∠C
=
180°,(三角形内角和定理)
而∠C
=
90°,
∴
∠A+∠B
=
90°.
三角形用什么符号表示的?那么直
角三角形又用什么符号表示呢?
三角形ABC表示为:
直角三角形可以用符号:
如图直角三角形ABC表示为:
△ABC
Rt△
Rt△ABC
例3:如图,∠C
=∠D
=90°,AD,BC
相交于点E,
∠CAE
与∠DBE
有什么关系?
C
D
E
A
B
∠CAE
=∠DBE
解:在Rt△ACE中,∠CAE=90°-∠AEC.
在Rt△ACE中,∠DBE=90°-∠BED
∵
∠AEC=∠BED
∴
∠CAE
=∠DBE
想一想:如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,有两个角互余的三角形是直角三角形吗?请说明理由.
已知:(如图)在△ABC中,
∠A+∠B
=
90°.
求证:△ABC是直角三角形.
证明:在△ABC中,
∠A+∠B+∠C
=?180°,(三角形内角和定理)
∵?∠A+∠B
=
90°,(已知)
∴?∠C
=
90°,
∴?△ABC是直角三角形.(直角三角形定义)
结论:有两个角互余的三角形是直角三角形.
教学目标
牛刀小试
如果一个三角形的两个内角分别是36°和54°,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
解析:第三个角是180°-36°-54°=90°,
∴三角形是直角三角形.
故选B.
不需要计算,你能得到答案吗?
B
教学目标
巩固提升
解析:设∠A=x°,则∠ABC=∠C=2x°,根据三角形内角和性质可知x+2x+2x=18°
解得x=36
∴∠C=2×36°=72°
在△BDC中,∵
BD是AC边上的高
∴∠BDC=90°;∴∠DBC=90°-72°;∴∠DBC=18°
1.已知△ABC中,∠ABC=∠C=2∠A
,BD是AC边上的高,求∠DBC的度数。
18°
解析:设此三角形的三个内角分别为x°、2x°、x°
则由三角形的内角和性质可知:x°+2x°+x°=180°。∴x=45°
则此三角形的三个内角分别为45°、90°、45°。
故答案选D。
2.一个三角形的三个内角的度数比是1:2:1,这个三角形是(
)?
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
D
解析:设∠A为x,则∠B=2∠A=2x,∠C=3∠A=3x
∵三角形的内角和为180°
∴x+2x+3x=180°,∴x=30°
则此三角形的三个内角为30°、60°、90°,故此三角形为直角三角形。
3.
在△ABC中,如果∠A=∠B=∠C,那么△ABC是什么三角形?
直角三角形
4.如图,△ABC中,∠ABC和∠ACB的平分线交于点O.
(1)
若∠ABC=60°,∠ACB=80°,求∠BOC的度数。
(2)
若∠A=70°,
求∠BOC的度数。
解:(1)∵∠ABC和∠ACB的平分线交于点O,
∠ABC=60°,∠ACB=80°
∴∠OBC=∠ABC=×60°=30°
∠OCB=∠ACB=×80°=40°
∵∠BOC+∠OCB+∠OBC=180°
∴∠BOC=180°-40°-30°=110°
(2)∵∠ABC和∠ACB的平分线交于点O,∴∠OBC=∠ABC,∠OCB=∠ACB
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)
∵∠A=70°∴∠ABC+∠ACB
=180°-∠A=180°-70°=110°
∴∠OBC+∠OCB=×110°=55°
∵∠BOC+∠OCB+∠OBC=180°
∴∠BOC=180°-55°=125°
5.如图,甲楼楼高16米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为45°,此时,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应当是多少米?
解:由题意可知:
∠ABC=90°,∠ACB=45°
∴∠BAC=180°-∠ABC-∠ACB
=180°-90°-45°
=45°
∴BC=AB=16米
答:两楼的距离是16米。
教学目标
课堂小结
1、三角形的内角和
2、三角形内角和性质
3、三角形的判断
