2021-2022学年人教版数学八年级上册11.2.2三角形的外角 课件(共43张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.2.2三角形的外角 课件(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览






文档简介
(共43张PPT)
11.2.2三角形的外角
学习目标
1.了解三角形的外角概念,经历探索三角形外角性质的过程。
2.通过探索三角形外角的性质,体会从特殊到一般的推理过程。
2、在△ABC中,
(1)∠C=90°,∠A=30
°,则∠B=____;
(2)∠A=50°,∠B=∠C,则∠B=_____.
1、三角形三个内角的和等于多少度?
65°
60°
三角形三个内角的和等于180°
温故而知新
三角形的内角是三角形内部的骄子
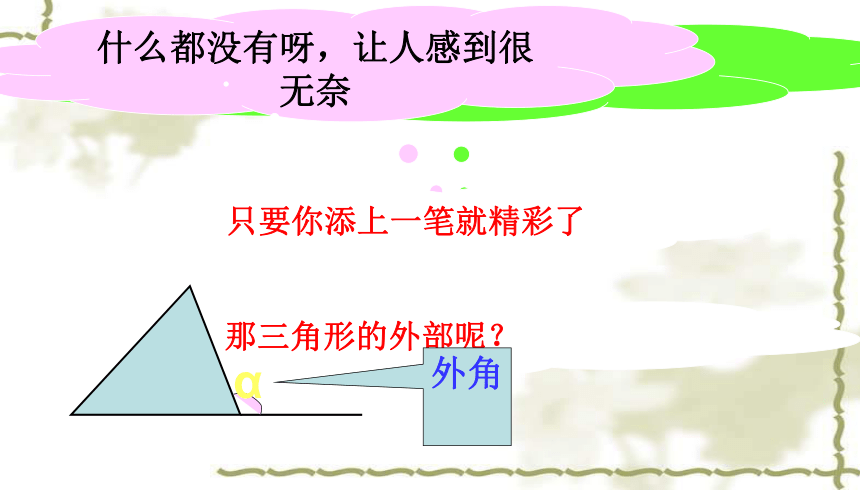
什么都没有呀,让人感到很无奈
那三角形的外部呢?
只要你添上一笔就精彩了
α
外角
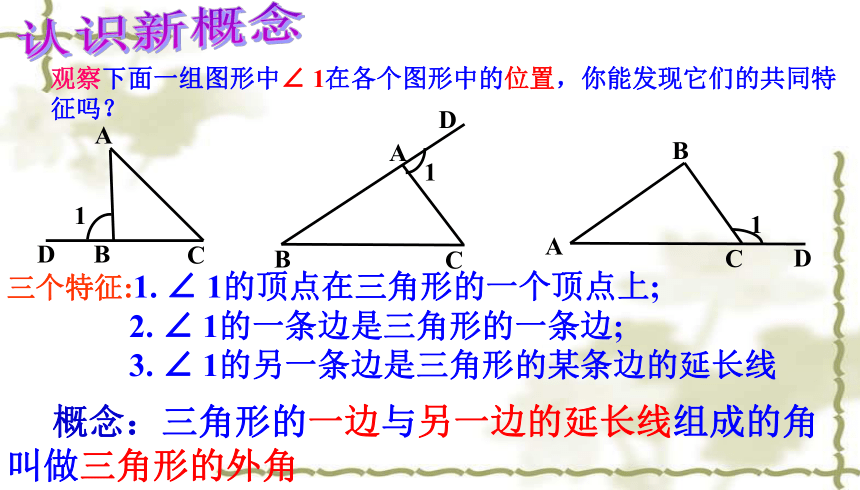
观察下面一组图形中∠
1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
概念:三角形的一边与另一边的延长线组成的角叫做三角形的外角
三个特征:1.
∠
1的顶点在三角形的一个顶点上;
2.
∠
1的一条边是三角形的一条边;
3.
∠
1的另一条边是三角形的某条边的延长线
认识新概念
大家一起画一画
想一想:
1、每一个三角形有几个外角?
2、每一个顶点处相对应的外角有几个?
3、这些外角中有几对外角相等?
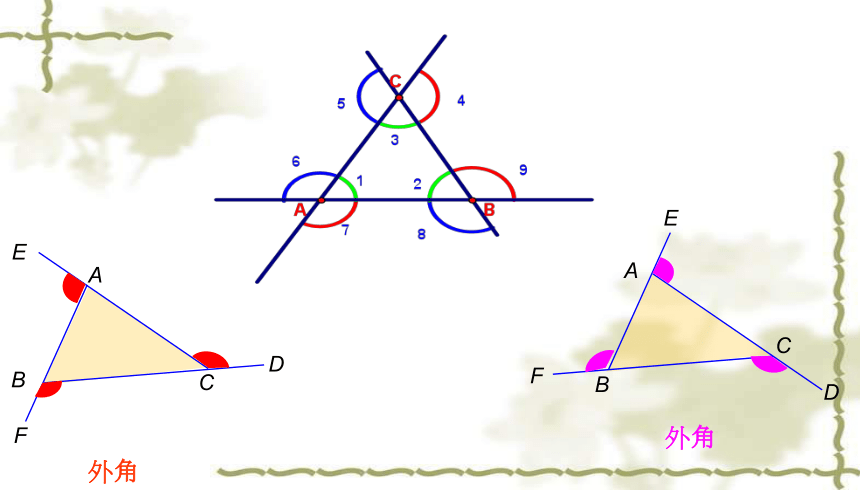
画一个三角形,再画出它所有的外角。
A
B
D
E
F
C
外角
A
B
D
E
F
C
外角
归纳:
1、每一个三角形都有6个外角;
2、每一个顶点相对应的外角都有2个;
3、这6个外角中有3对外角相等。
A
B
D
E
F
C
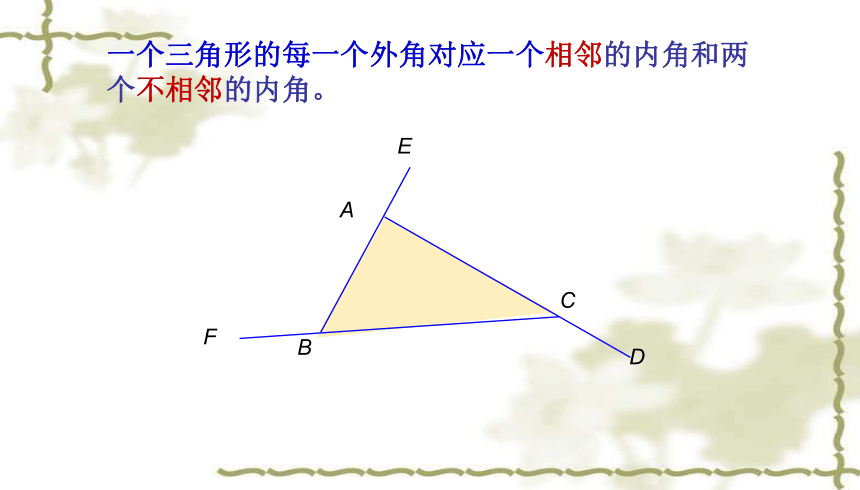
一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角。
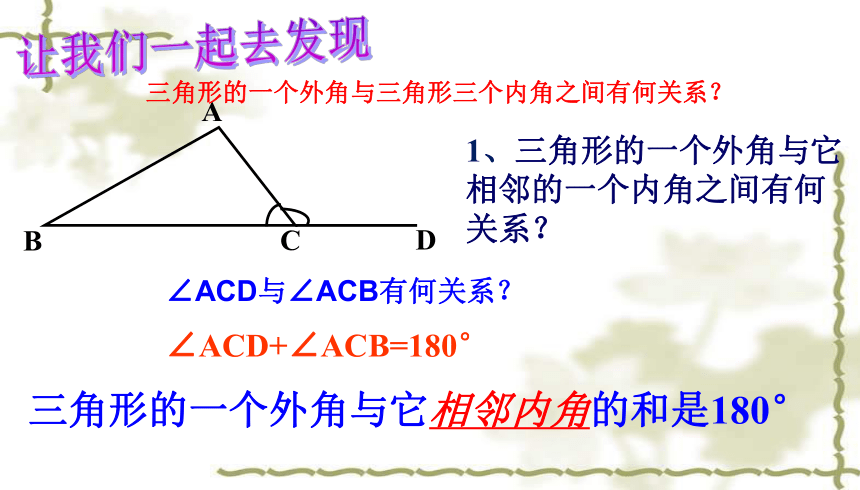
1、三角形的一个外角与它相邻的一个内角之间有何关系?
∠ACD+∠ACB=180°
A
B
C
D
让我们一起去发现
三角形的一个外角与三角形三个内角之间有何关系?
三角形的一个外角与它相邻内角的和是180°
∠ACD与∠ACB有何关系?
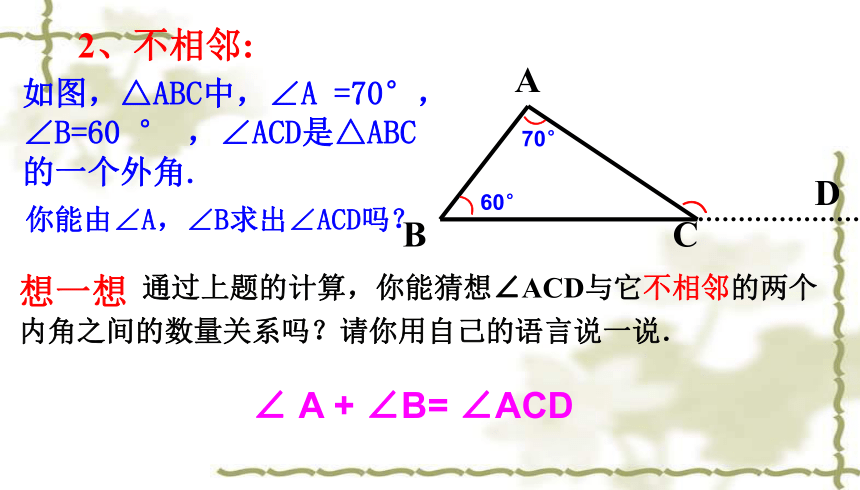
2.三角形的一个外角与它不相邻的两个内角之间有何关系?
想一想:
如图,△ABC中,∠A
=70°,∠B=60
°
,∠ACD是△ABC的一个外角.
你能由∠A,∠B求出∠ACD吗?
2、不相邻:
A
B
C
D
⌒
70°
60°
⌒
⌒
通过上题的计算,你能猜想∠ACD与它不相邻的两个内角之间的数量关系吗?请你用自己的语言说一说.
想一想
∠
A
+
∠B=
∠ACD
任意三角形的一个外角与它不相邻的两个内角是否都有这种关系?
试一试
你能行
D
A
B
C
方法1
证明:
∠A
+
∠B
+
∠ACB=1800
∠ACD
+
∠ACB=1800
∠
A
+
∠B=
∠ACD
试证明:
∠
A
+
∠B=
∠ACD
D
证明:过C作CE
//AB
A
B
C
1
2
∠1=
∠B
∠2=
∠A
∠1+
∠2=
∠A+
∠B
即∠ACD=
∠A+
∠B
E
方法2
结论:
三角形的一个外角等于与它不相邻的两个内角的和。
三角形外角的性质:
三角形的一个外角等于
与它不相邻的两个内角的和。
几何语言:
∠CAD是三角形ABC的外角
∠B+∠C=∠CAD
A
B
C
D
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>).
三角形的一个外角大于与它不相邻的任何一个内角。
A
C
B
D
>
>
你选谁
?
结论:
变式
已知:如图6-14,在△ABC中,
∠1是它的一个外角,
E为边AC上一点,延长BC到D,连接DE.
求证:
∠1>∠2.
证明:∵
∠1是△ABC的一个外角(已知),
∴
∠1>∠3(三角形的一个外角大于任何一个和
它不相邻的内角).
∵∠3是△CDE的一个外角
(外角定义).
∴∠3>∠2(三角形的一个外角大于任何一个和
它不相邻的内角).
∴
∠1>∠2(不等式的性质).
C
A
B
F
1
3
4
5
E
D
2
1、说出下列图形中∠1的度数:
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90?
85?
95?
训练基地
∠C
∠3
∠DAC
∠4
2
、
如图,口答:
(1)∠1
=
+
;
(2)∠2
=
+
.
B
A
C
D
1
2
3
4
学有所用
例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
1、
如图所示,∠A=31°,∠B=45°,∠C=38°,则∠DFE=
.
练习
2、
三角形一个外角小于与它相邻的内角,这个三角形( )
A
、是直角三角形
B
、是锐角三角形
C
、是钝角三角形
D
、属于哪一类不能确定
3、
等腰三角形一个外角等于100°,求这个三角形的各个内角
。
80°
80°
20°
80°
50°
50°
C
4
、如图,直线AB∥CD,直线EF分别与AB、CD相交,则有( )
A
、∠1+∠2-∠3=180°
?B
、∠1-∠2+∠3=180°
?C
、∠3+∠2-∠1=180°
?D
、∠1+∠2+∠3=180°
教科书习题11.2第6、8
,11题.
11.如图,CE是△ABC的外角∠ACD
的角平分线,且CE交BA的延长线于点E,求证∠BAC=
∠B+2
∠E
运用三角形的外角的性质
例2
如图,∠BAE,∠CBF,∠ACD
是△ABC
的三个外角,它们的和是多少?
解法一:∵ ∠BAE
=∠2
+∠3,
∠CBF
=∠1
+∠3,
∠ACD
=∠1
+∠2,
∴ ∠BAE
+∠CBF
+∠ACD
=
(∠2
+∠3)+(∠1
+∠3)+
(∠1
+∠2)
A
B
F
C
D
E
1
2
3
=
2(∠1
+∠2
+∠3).
∵ ∠1
+∠2
+∠3
=180°,
∴ ∠BAE
+∠CBF
+∠ACD
=
2×180°=360°.
解法二:
∵∠1
+∠BAE
=180°,
∠2
+∠CBF
=180°,
∠3
+∠ACD
=180°,
∴∠1
+∠2
+∠3
+
∠BAE
+∠CBF
+∠ACD
=
540°.
A
B
F
C
D
E
1
2
3
∵∠1
+
∠2
+
∠3
=180°,
∴∠BAE
+
∠CBF
+
∠ACD
=
540°-
180°
=360°.
从与每一个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
三角形的外角和:
三角形的外角和等于360
?
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
1
2
3
360°
N
P
M
拓展延伸
例3.一个零件的形状如图,按规定∠A应等于90°,∠B、∠D应分别是30°和20°,李叔叔量得∠BCD=142°,就断定这个零件不合格,你能说出道理吗?
拓展提高
提示:可以先计算出合格时∠BDC的度数,但是∠BDC与∠A
、∠B、
∠C不在同一个三角形内,因而无法找到它们之间的数量关系,因此需要添加辅助线。那如何添加辅助线才能建立这几个角之间的联系呢?
解法1:延长BC交AD于点E,
∠DEB=∠A+∠B=120°,
∠DCB=∠DEB+∠D
=120°+20°=140°
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
∵∠A=90°,∠B=30°
在△ABE中
在△CDE中
点拨:也可以延长DC与AB交于一点,方法与此相同.
解法2:连接AC并延长至E,
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
∵∠DAB=90°,∠B=30°,∠D=20°
在△ADC中
在△ACB中
∠3=∠1+∠D
∠4=∠2+∠B
∠
DCB=∠3+∠4
=∠1+∠D+∠2+∠B=140°
解法3:过点C作EF∥AB,交AD于E,
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
在△EDC中
∴∠1=∠DEC+∠D=1100
∴∠B=∠2=
30°
∴∠
DCB=∠1+∠2=140°
∴∠DEC=∠A=90°
1
2
∵∠D=200
解法4:连接BD,
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
在△ADB中
∴∠
A
+∠3
+∠1
+∠4+∠2=180°
1
2
3
4
∵∠A=90°,∠B=30°,∠D=20°
∴∠1
+∠2=40°
在△CDB中
∴∠1
+∠C+∠2=180°
∴∠C=140°
第35页
广角变式
第36页
国旗上的数学
三角形的一个外角的性质
(3)三角形的一个外角大于任何一个与它不相邻的内角。
(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
(4)三角形的外角和是360°
一.判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。
(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。
(
)
自我检测
8、如图所示,在△ABC中,∠A=α,△ABC的内角平分线或外角平分线交于点P,
且∠P=β,试探求下列各图中α与β的关系,并选择一个加以说明.
9.已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:__________;
(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数;(写出解答过程)
(3)如果图2中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系.(直接写出结论即可)
10.如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
11.如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2= _________ .
12、如图所示,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.
11.2.2三角形的外角
学习目标
1.了解三角形的外角概念,经历探索三角形外角性质的过程。
2.通过探索三角形外角的性质,体会从特殊到一般的推理过程。
2、在△ABC中,
(1)∠C=90°,∠A=30
°,则∠B=____;
(2)∠A=50°,∠B=∠C,则∠B=_____.
1、三角形三个内角的和等于多少度?
65°
60°
三角形三个内角的和等于180°
温故而知新
三角形的内角是三角形内部的骄子
什么都没有呀,让人感到很无奈
那三角形的外部呢?
只要你添上一笔就精彩了
α
外角
观察下面一组图形中∠
1在各个图形中的位置,你能发现它们的共同特征吗?
B
C
A
1
D
A
C
B
1
D
A
C
B
1
D
概念:三角形的一边与另一边的延长线组成的角叫做三角形的外角
三个特征:1.
∠
1的顶点在三角形的一个顶点上;
2.
∠
1的一条边是三角形的一条边;
3.
∠
1的另一条边是三角形的某条边的延长线
认识新概念
大家一起画一画
想一想:
1、每一个三角形有几个外角?
2、每一个顶点处相对应的外角有几个?
3、这些外角中有几对外角相等?
画一个三角形,再画出它所有的外角。
A
B
D
E
F
C
外角
A
B
D
E
F
C
外角
归纳:
1、每一个三角形都有6个外角;
2、每一个顶点相对应的外角都有2个;
3、这6个外角中有3对外角相等。
A
B
D
E
F
C
一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角。
1、三角形的一个外角与它相邻的一个内角之间有何关系?
∠ACD+∠ACB=180°
A
B
C
D
让我们一起去发现
三角形的一个外角与三角形三个内角之间有何关系?
三角形的一个外角与它相邻内角的和是180°
∠ACD与∠ACB有何关系?
2.三角形的一个外角与它不相邻的两个内角之间有何关系?
想一想:
如图,△ABC中,∠A
=70°,∠B=60
°
,∠ACD是△ABC的一个外角.
你能由∠A,∠B求出∠ACD吗?
2、不相邻:
A
B
C
D
⌒
70°
60°
⌒
⌒
通过上题的计算,你能猜想∠ACD与它不相邻的两个内角之间的数量关系吗?请你用自己的语言说一说.
想一想
∠
A
+
∠B=
∠ACD
任意三角形的一个外角与它不相邻的两个内角是否都有这种关系?
试一试
你能行
D
A
B
C
方法1
证明:
∠A
+
∠B
+
∠ACB=1800
∠ACD
+
∠ACB=1800
∠
A
+
∠B=
∠ACD
试证明:
∠
A
+
∠B=
∠ACD
D
证明:过C作CE
//AB
A
B
C
1
2
∠1=
∠B
∠2=
∠A
∠1+
∠2=
∠A+
∠B
即∠ACD=
∠A+
∠B
E
方法2
结论:
三角形的一个外角等于与它不相邻的两个内角的和。
三角形外角的性质:
三角形的一个外角等于
与它不相邻的两个内角的和。
几何语言:
∠CAD是三角形ABC的外角
∠B+∠C=∠CAD
A
B
C
D
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>).
三角形的一个外角大于与它不相邻的任何一个内角。
A
C
B
D
>
>
你选谁
?
结论:
变式
已知:如图6-14,在△ABC中,
∠1是它的一个外角,
E为边AC上一点,延长BC到D,连接DE.
求证:
∠1>∠2.
证明:∵
∠1是△ABC的一个外角(已知),
∴
∠1>∠3(三角形的一个外角大于任何一个和
它不相邻的内角).
∵∠3是△CDE的一个外角
(外角定义).
∴∠3>∠2(三角形的一个外角大于任何一个和
它不相邻的内角).
∴
∠1>∠2(不等式的性质).
C
A
B
F
1
3
4
5
E
D
2
1、说出下列图形中∠1的度数:
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90?
85?
95?
训练基地
∠C
∠3
∠DAC
∠4
2
、
如图,口答:
(1)∠1
=
+
;
(2)∠2
=
+
.
B
A
C
D
1
2
3
4
学有所用
例1:如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
1、
如图所示,∠A=31°,∠B=45°,∠C=38°,则∠DFE=
.
练习
2、
三角形一个外角小于与它相邻的内角,这个三角形( )
A
、是直角三角形
B
、是锐角三角形
C
、是钝角三角形
D
、属于哪一类不能确定
3、
等腰三角形一个外角等于100°,求这个三角形的各个内角
。
80°
80°
20°
80°
50°
50°
C
4
、如图,直线AB∥CD,直线EF分别与AB、CD相交,则有( )
A
、∠1+∠2-∠3=180°
?B
、∠1-∠2+∠3=180°
?C
、∠3+∠2-∠1=180°
?D
、∠1+∠2+∠3=180°
教科书习题11.2第6、8
,11题.
11.如图,CE是△ABC的外角∠ACD
的角平分线,且CE交BA的延长线于点E,求证∠BAC=
∠B+2
∠E
运用三角形的外角的性质
例2
如图,∠BAE,∠CBF,∠ACD
是△ABC
的三个外角,它们的和是多少?
解法一:∵ ∠BAE
=∠2
+∠3,
∠CBF
=∠1
+∠3,
∠ACD
=∠1
+∠2,
∴ ∠BAE
+∠CBF
+∠ACD
=
(∠2
+∠3)+(∠1
+∠3)+
(∠1
+∠2)
A
B
F
C
D
E
1
2
3
=
2(∠1
+∠2
+∠3).
∵ ∠1
+∠2
+∠3
=180°,
∴ ∠BAE
+∠CBF
+∠ACD
=
2×180°=360°.
解法二:
∵∠1
+∠BAE
=180°,
∠2
+∠CBF
=180°,
∠3
+∠ACD
=180°,
∴∠1
+∠2
+∠3
+
∠BAE
+∠CBF
+∠ACD
=
540°.
A
B
F
C
D
E
1
2
3
∵∠1
+
∠2
+
∠3
=180°,
∴∠BAE
+
∠CBF
+
∠ACD
=
540°-
180°
=360°.
从与每一个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。
三角形的外角和:
三角形的外角和等于360
?
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
1
2
3
360°
N
P
M
拓展延伸
例3.一个零件的形状如图,按规定∠A应等于90°,∠B、∠D应分别是30°和20°,李叔叔量得∠BCD=142°,就断定这个零件不合格,你能说出道理吗?
拓展提高
提示:可以先计算出合格时∠BDC的度数,但是∠BDC与∠A
、∠B、
∠C不在同一个三角形内,因而无法找到它们之间的数量关系,因此需要添加辅助线。那如何添加辅助线才能建立这几个角之间的联系呢?
解法1:延长BC交AD于点E,
∠DEB=∠A+∠B=120°,
∠DCB=∠DEB+∠D
=120°+20°=140°
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
∵∠A=90°,∠B=30°
在△ABE中
在△CDE中
点拨:也可以延长DC与AB交于一点,方法与此相同.
解法2:连接AC并延长至E,
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
∵∠DAB=90°,∠B=30°,∠D=20°
在△ADC中
在△ACB中
∠3=∠1+∠D
∠4=∠2+∠B
∠
DCB=∠3+∠4
=∠1+∠D+∠2+∠B=140°
解法3:过点C作EF∥AB,交AD于E,
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
在△EDC中
∴∠1=∠DEC+∠D=1100
∴∠B=∠2=
30°
∴∠
DCB=∠1+∠2=140°
∴∠DEC=∠A=90°
1
2
∵∠D=200
解法4:连接BD,
若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格
在△ADB中
∴∠
A
+∠3
+∠1
+∠4+∠2=180°
1
2
3
4
∵∠A=90°,∠B=30°,∠D=20°
∴∠1
+∠2=40°
在△CDB中
∴∠1
+∠C+∠2=180°
∴∠C=140°
第35页
广角变式
第36页
国旗上的数学
三角形的一个外角的性质
(3)三角形的一个外角大于任何一个与它不相邻的内角。
(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
(4)三角形的外角和是360°
一.判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。
(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。
(
)
自我检测
8、如图所示,在△ABC中,∠A=α,△ABC的内角平分线或外角平分线交于点P,
且∠P=β,试探求下列各图中α与β的关系,并选择一个加以说明.
9.已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:__________;
(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数;(写出解答过程)
(3)如果图2中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系.(直接写出结论即可)
10.如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
11.如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2= _________ .
12、如图所示,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.
