2021—2022学年苏科版数学八年级上册1.3 探索三角形全等的条件(5) 课件(共16张PPT)
文档属性
| 名称 | 2021—2022学年苏科版数学八年级上册1.3 探索三角形全等的条件(5) 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 246.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 07:53:53 | ||
图片预览



文档简介
(共16张PPT)
第1章
全等三角形
1.3 探索三角形全等的条件(5)
复习提问
1、什么叫做全等三角形?怎样表示?
2、全等三角形的性质?
3、怎样判断两个三角形全等?
角边角
ASA
角角边
AAS
边角边
SAS
两边和其中一边的对角对应相等的两个三角形不一定全等
SSA
\
=
\
=
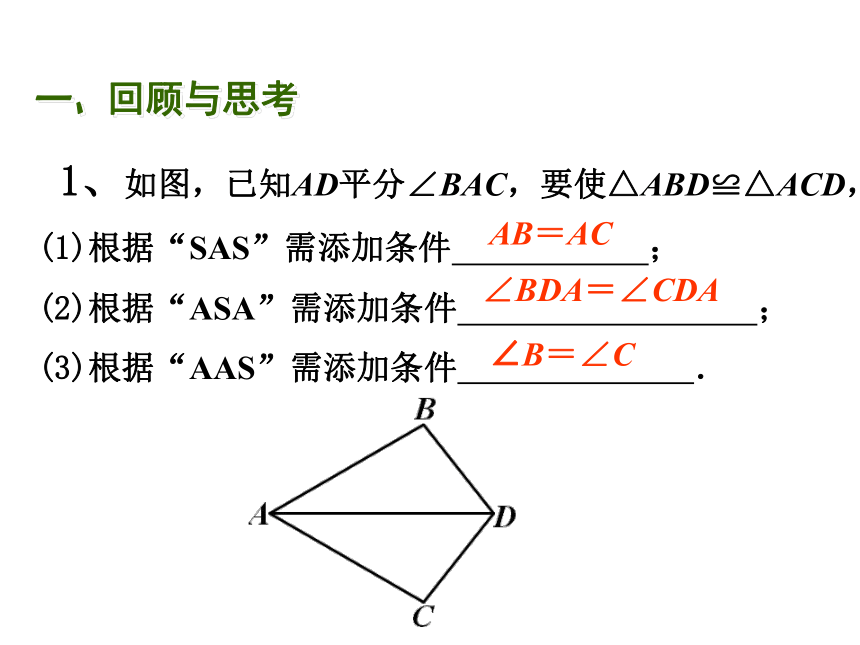
1、如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件
;
(2)根据“ASA”需添加条件
;
(3)根据“AAS”需添加条件
.
AB=AC
∠BDA=∠CDA
∠B=∠C
一、回顾与思考
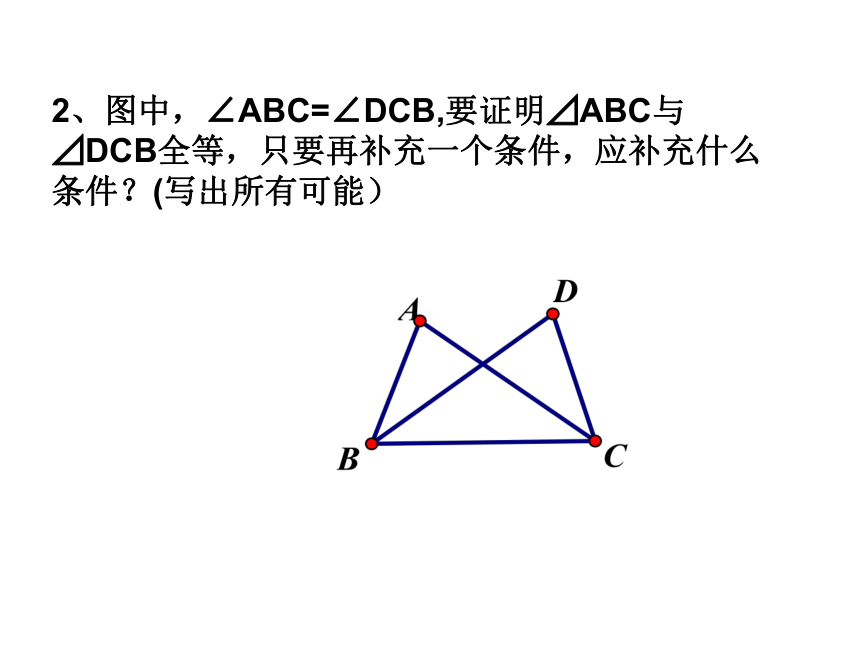
2、图中,∠ABC=∠DCB,要证明⊿ABC与⊿DCB全等,只要再补充一个条件,应补充什么条件?(写出所有可能)
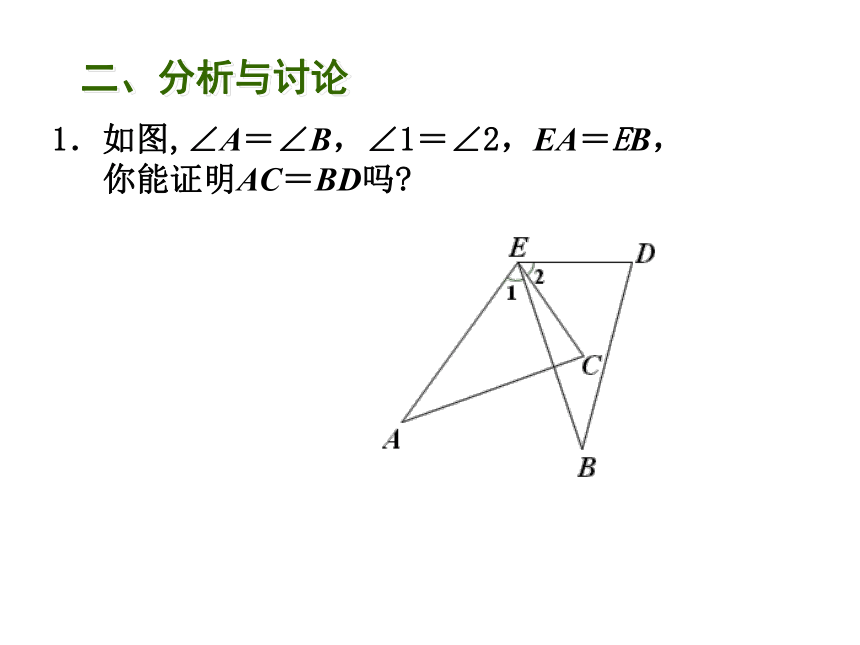
1.如图,∠A=∠B,∠1=∠2,EA=EB,
你能证明AC=BD吗?
二、分析与讨论
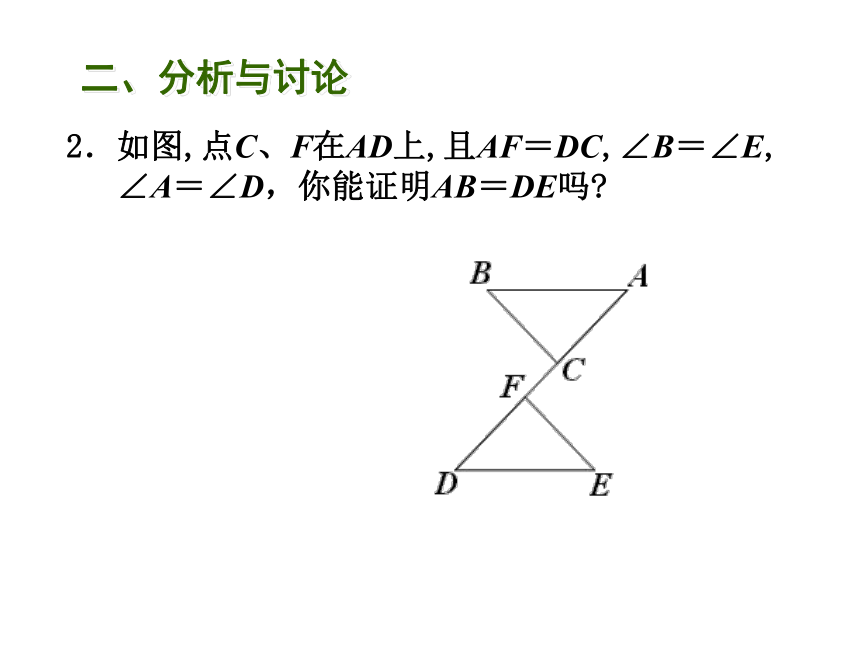
2.如图,点C、F在AD上,且AF=DC,∠B=∠E,
∠A=∠D,你能证明AB=DE吗?
二、分析与讨论
3、
已知:如图CD⊥AB,EF⊥AB,垂足分别为D、
F,CD=EF,AD=BF.
求证:∠A=∠B
4、
已知:如图,点A、B、C、D在一条直线上,
EA∥FB,EC∥FD,EA=FB.
求证:AB=CD.
上面的推理过程可以用符号“?”简明地表述如下:
EA∥FB?∠A=∠FBD
EC∥FD?∠ECA=∠D
?
△EAC≌△FBD
EA=FB
?AC=BD?AB+BC=CD+BC?AB=CD
已知:如图∠1=∠2=90°,AD=AE,那么图中有哪些全等三角形?并加以证明。
5、
6、已知:如图,AB=AC,点D、E分别在AB、
AC上,∠B=∠C.
求证:DB=EC
.
变式一
已知:∠1=∠2,∠B=∠C,AB=AC.
求证:AD=AE
,∠D=∠E.
1
2
变式二
已知:∠1=∠2,∠B=∠C,AB
=AC,
D、A、E在一条直线上.
求证:AD
=AE,∠D
=∠E.
1
2
7、已知:如图,AC⊥AB,BD⊥AB,CE⊥DE,
CE
=
DE
.
求证:AC+BD
=
AB.
8、已知:如图,∠ABC=90°,AB=BC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E、F.
求证:EF+AE=CF.
第1章
全等三角形
1.3 探索三角形全等的条件(5)
复习提问
1、什么叫做全等三角形?怎样表示?
2、全等三角形的性质?
3、怎样判断两个三角形全等?
角边角
ASA
角角边
AAS
边角边
SAS
两边和其中一边的对角对应相等的两个三角形不一定全等
SSA
\
=
\
=
1、如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件
;
(2)根据“ASA”需添加条件
;
(3)根据“AAS”需添加条件
.
AB=AC
∠BDA=∠CDA
∠B=∠C
一、回顾与思考
2、图中,∠ABC=∠DCB,要证明⊿ABC与⊿DCB全等,只要再补充一个条件,应补充什么条件?(写出所有可能)
1.如图,∠A=∠B,∠1=∠2,EA=EB,
你能证明AC=BD吗?
二、分析与讨论
2.如图,点C、F在AD上,且AF=DC,∠B=∠E,
∠A=∠D,你能证明AB=DE吗?
二、分析与讨论
3、
已知:如图CD⊥AB,EF⊥AB,垂足分别为D、
F,CD=EF,AD=BF.
求证:∠A=∠B
4、
已知:如图,点A、B、C、D在一条直线上,
EA∥FB,EC∥FD,EA=FB.
求证:AB=CD.
上面的推理过程可以用符号“?”简明地表述如下:
EA∥FB?∠A=∠FBD
EC∥FD?∠ECA=∠D
?
△EAC≌△FBD
EA=FB
?AC=BD?AB+BC=CD+BC?AB=CD
已知:如图∠1=∠2=90°,AD=AE,那么图中有哪些全等三角形?并加以证明。
5、
6、已知:如图,AB=AC,点D、E分别在AB、
AC上,∠B=∠C.
求证:DB=EC
.
变式一
已知:∠1=∠2,∠B=∠C,AB=AC.
求证:AD=AE
,∠D=∠E.
1
2
变式二
已知:∠1=∠2,∠B=∠C,AB
=AC,
D、A、E在一条直线上.
求证:AD
=AE,∠D
=∠E.
1
2
7、已知:如图,AC⊥AB,BD⊥AB,CE⊥DE,
CE
=
DE
.
求证:AC+BD
=
AB.
8、已知:如图,∠ABC=90°,AB=BC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E、F.
求证:EF+AE=CF.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
