2.2.2法拉第电磁感应定律 课件(16张PPT)
文档属性
| 名称 | 2.2.2法拉第电磁感应定律 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览





文档简介
2.2.2 法拉第电磁感应定律
1.感应电动势
(1)定义:在电磁感应现象中产生的电动势。
(2)感应电动势与感应电流的关系
产生感应电动势的部分导体相当于电源,闭合导体回路中有感应电动势就有感应电流,若导体回路不闭合,则没有感应电流,但仍有感应电动势。
2.法拉第电磁感应定律
内容:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。
1. 怎样算出感应电动势?
2. 怎样推导导线切割磁感线时的感应电动势的表达式?
教师和学生一起回顾上节课的内容中。我们知道闭合电路中都产生了感应电流,电路中必须要有电源,电源提供了电动势,从而产生电流。在电磁感应现象中产生的电动势叫做感应电动势。那么感应电动势的大小跟哪些因素有关呢?我们用一个导体棒切割磁感线的感应电动势,这个过程中线框的面积变化量是什么呢?本节课我们就来共同研究这个问题?
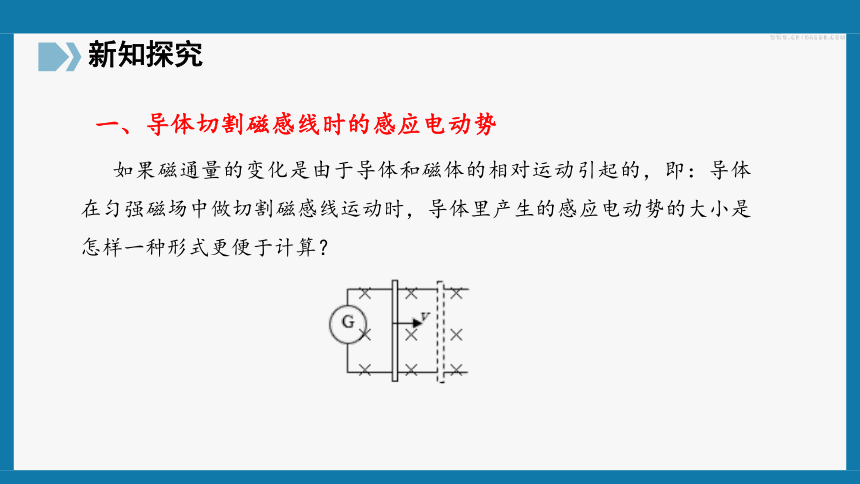
如果磁通量的变化是由于导体和磁体的相对运动引起的,即:导体在匀强磁场中做切割磁感线运动时,导体里产生的感应电动势的大小是怎样一种形式更便于计算?
一、导体切割磁感线时的感应电动势
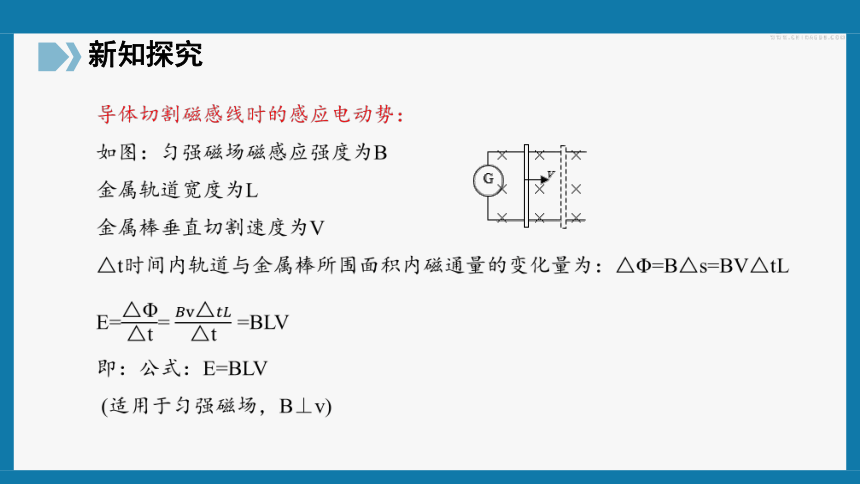
导体切割磁感线时的感应电动势:
如图:匀强磁场磁感应强度为B
金属轨道宽度为L
金属棒垂直切割速度为V
△t时间内轨道与金属棒所围面积内磁通量的变化量为:△Φ=B△s=BV△tL
E=△Φ△t= ????????△????????△t =BLV
即:公式:E=BLV
(适用于匀强磁场,B⊥v)
?
若B与V有夹角θ如图。
分解V,或分解B
与B平行的分量V2=Vcosθ,没有切割磁感线,不产生电动势
与B垂直的分量V1=Vsinθ,切割磁感线产生电动势E=BLVsinθ
结论:导体切割磁感线时,产生的感应电动势的大小,跟磁感应强度B、导线长度L、运动速度v以及运动方向和磁感应强度方向的夹角θ的正弦sinθ成正比。
公式:E=BLVsinθ
B
v2
v1
v11
注意:
①这是法拉第电磁感应定律的第一个推论。
②公式中V为导体棒和磁场的相对运动速度。
③公式中的单位分别是:V,T,m。m/s
1V=lT×1m×1m/s
一段导线在做切割磁感线的运动时相当于一个电源,通过上面的分析可以看到,这时的非静电力与洛伦兹力有关。
在图 2.2-2 中,由于导体棒运动产生感应电动势,电路中有电流通过,导体棒在运动过程中会受到安培力的作用。可以判断,安培力的方向与推动导体棒运动的力的方向是相反的。这时即使导体棒做匀速运动,推力也做功。如果没有推力的作用,导体棒将克服安培力做功而消耗本身的机械能。
总结:如果感应电动势是由于导体运动而产生的,它也叫作动生电动势。
例1.竖直向下的匀强磁场中,将一水平放置的金属棒ab以水平初速度V0抛出,设在整个过程中,棒始终平动且空气阻力不计,则在金属棒运动过程中产生的感应电动势大小变化情况是( )
A.越来越大 B.越来越小 C.保持不变 D.无法判断
C
解析:金属棒ab做平抛运动,其水平方向的分运动是匀速直线运动,水平分速度保持不变,等于v0.由感应电动势公式E=Blvsinα,vsinα是垂直于磁感线方向的分速度,即是平抛运动的水平分速度,等于v0,则感应电动势E=Blv0,B、l、v0均不变,则感应电动势大小保持不变。则C正确。
故选:C。
如图所示,PQRS为一正方形导线框,它以恒定速度向右进入以MN为边界的匀强磁场,磁场方向垂直线框平面,MN线与线框的边成45°角,E、F分别为PS和PQ的中点,关于线框中的感应电流,下列说法正确的是( )
A.当E点经过边界MN时,感应电流最大
B.当P点经过边界MN时,感应电流最大
C.当F点经过边界MN时,感应电流最大
D.当Q点经过边界MN时,感应电流最大
变式训练:
B
一段导线在做切割磁感线的运动时相当于一个电源,通过上面的分析可以看到,这时的非静电力与洛伦兹力有关。
技法点拨:
导体切割磁感线时的感应电动势:
如图:匀强磁场磁感应强度为B
金属轨道宽度为L
金属棒垂直切割速度为V
△t时间内轨道与金属棒所围面积内磁通量的变化量为:△Φ=B△s=BV△tL
E=△Φ△t= ????????△????????△t =BLV
即:公式:E=BLV
(适用于匀强磁场,B⊥v)
?
若B与V有夹角θ如图
B
v2
v1
v
分解V,或分解B
与B平行的分量V2=Vcosθ,没有切割磁感线,不产生电动势
与B垂直的分量V1=Vsinθ,切割磁感线产生电动势E=BLVsinθ
结论:导体切割磁感线时,产生的感应电动势的大小,跟磁感应强度B、导线长度L、运动速度v以及运动方向和磁感应强度方向的夹角θ的正弦sinθ成正比。
公式:E=BLVsinθ
再见
1.感应电动势
(1)定义:在电磁感应现象中产生的电动势。
(2)感应电动势与感应电流的关系
产生感应电动势的部分导体相当于电源,闭合导体回路中有感应电动势就有感应电流,若导体回路不闭合,则没有感应电流,但仍有感应电动势。
2.法拉第电磁感应定律
内容:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比。
1. 怎样算出感应电动势?
2. 怎样推导导线切割磁感线时的感应电动势的表达式?
教师和学生一起回顾上节课的内容中。我们知道闭合电路中都产生了感应电流,电路中必须要有电源,电源提供了电动势,从而产生电流。在电磁感应现象中产生的电动势叫做感应电动势。那么感应电动势的大小跟哪些因素有关呢?我们用一个导体棒切割磁感线的感应电动势,这个过程中线框的面积变化量是什么呢?本节课我们就来共同研究这个问题?
如果磁通量的变化是由于导体和磁体的相对运动引起的,即:导体在匀强磁场中做切割磁感线运动时,导体里产生的感应电动势的大小是怎样一种形式更便于计算?
一、导体切割磁感线时的感应电动势
导体切割磁感线时的感应电动势:
如图:匀强磁场磁感应强度为B
金属轨道宽度为L
金属棒垂直切割速度为V
△t时间内轨道与金属棒所围面积内磁通量的变化量为:△Φ=B△s=BV△tL
E=△Φ△t= ????????△????????△t =BLV
即:公式:E=BLV
(适用于匀强磁场,B⊥v)
?
若B与V有夹角θ如图。
分解V,或分解B
与B平行的分量V2=Vcosθ,没有切割磁感线,不产生电动势
与B垂直的分量V1=Vsinθ,切割磁感线产生电动势E=BLVsinθ
结论:导体切割磁感线时,产生的感应电动势的大小,跟磁感应强度B、导线长度L、运动速度v以及运动方向和磁感应强度方向的夹角θ的正弦sinθ成正比。
公式:E=BLVsinθ
B
v2
v1
v11
注意:
①这是法拉第电磁感应定律的第一个推论。
②公式中V为导体棒和磁场的相对运动速度。
③公式中的单位分别是:V,T,m。m/s
1V=lT×1m×1m/s
一段导线在做切割磁感线的运动时相当于一个电源,通过上面的分析可以看到,这时的非静电力与洛伦兹力有关。
在图 2.2-2 中,由于导体棒运动产生感应电动势,电路中有电流通过,导体棒在运动过程中会受到安培力的作用。可以判断,安培力的方向与推动导体棒运动的力的方向是相反的。这时即使导体棒做匀速运动,推力也做功。如果没有推力的作用,导体棒将克服安培力做功而消耗本身的机械能。
总结:如果感应电动势是由于导体运动而产生的,它也叫作动生电动势。
例1.竖直向下的匀强磁场中,将一水平放置的金属棒ab以水平初速度V0抛出,设在整个过程中,棒始终平动且空气阻力不计,则在金属棒运动过程中产生的感应电动势大小变化情况是( )
A.越来越大 B.越来越小 C.保持不变 D.无法判断
C
解析:金属棒ab做平抛运动,其水平方向的分运动是匀速直线运动,水平分速度保持不变,等于v0.由感应电动势公式E=Blvsinα,vsinα是垂直于磁感线方向的分速度,即是平抛运动的水平分速度,等于v0,则感应电动势E=Blv0,B、l、v0均不变,则感应电动势大小保持不变。则C正确。
故选:C。
如图所示,PQRS为一正方形导线框,它以恒定速度向右进入以MN为边界的匀强磁场,磁场方向垂直线框平面,MN线与线框的边成45°角,E、F分别为PS和PQ的中点,关于线框中的感应电流,下列说法正确的是( )
A.当E点经过边界MN时,感应电流最大
B.当P点经过边界MN时,感应电流最大
C.当F点经过边界MN时,感应电流最大
D.当Q点经过边界MN时,感应电流最大
变式训练:
B
一段导线在做切割磁感线的运动时相当于一个电源,通过上面的分析可以看到,这时的非静电力与洛伦兹力有关。
技法点拨:
导体切割磁感线时的感应电动势:
如图:匀强磁场磁感应强度为B
金属轨道宽度为L
金属棒垂直切割速度为V
△t时间内轨道与金属棒所围面积内磁通量的变化量为:△Φ=B△s=BV△tL
E=△Φ△t= ????????△????????△t =BLV
即:公式:E=BLV
(适用于匀强磁场,B⊥v)
?
若B与V有夹角θ如图
B
v2
v1
v
分解V,或分解B
与B平行的分量V2=Vcosθ,没有切割磁感线,不产生电动势
与B垂直的分量V1=Vsinθ,切割磁感线产生电动势E=BLVsinθ
结论:导体切割磁感线时,产生的感应电动势的大小,跟磁感应强度B、导线长度L、运动速度v以及运动方向和磁感应强度方向的夹角θ的正弦sinθ成正比。
公式:E=BLVsinθ
再见
