1.5弹性碰撞和非弹性碰撞 课件(28张PPT)
文档属性
| 名称 | 1.5弹性碰撞和非弹性碰撞 课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览








文档简介
1.5 弹性碰撞和非弹性碰撞
1. 了解弹性碰撞和非弹性碰撞。
2.会分析具体实例中的碰撞特点及类型。
3.知道对心碰撞和非对心碰撞,加深对动量守恒定律和机械能守恒定律的理解。
学习重点:掌握什么是弹性碰撞、非弹性碰撞和完全非弹性碰撞。
学习难点:分析具体实例、碰撞可能发生的判定
思考:碰撞是自然界中常见的现象,你能列举出一些碰撞现象吗?
汽车之间的碰撞
网球和球拍的碰撞
肢体之间的碰撞
陨石撞击地球
水上电动碰碰船
思考:那么如果从能量的角度去研究碰撞前后物体动能的变化,该如何对碰撞进行分类呢?
大部分物体碰撞的特点:
1.相互作用时间极短。
2.相互作用力极大,即内力远大于外力,遵循动量守恒定律。
一、弹性碰撞和非弹性碰撞
研究小车碰撞前后的动能变化
如图滑轨上有两辆安装了弹性碰撞架的小车,它们发生碰撞后改变了运动状态。测量两辆小车的质量以及它们碰撞前后的速度,研究碰撞前后总动能的变化情况。
研究两辆小车碰撞前后总动能的变化情况
碰撞前
碰撞后
质量
m1=0.10kg
m2=0.15kg
m1=0.10kg
m2=0.15kg
速度
V1=0.4m/s
V2=-0.2m/s
V1?=-0.32m/s
V2?=0.28m/s
12mv2
12m1v12+12m2v22=
12m1v1?2+12m2v2?2=
0.011J
0.011J
通过实验可以发现,在上述实验条件下,碰撞前后总动能基本不变。
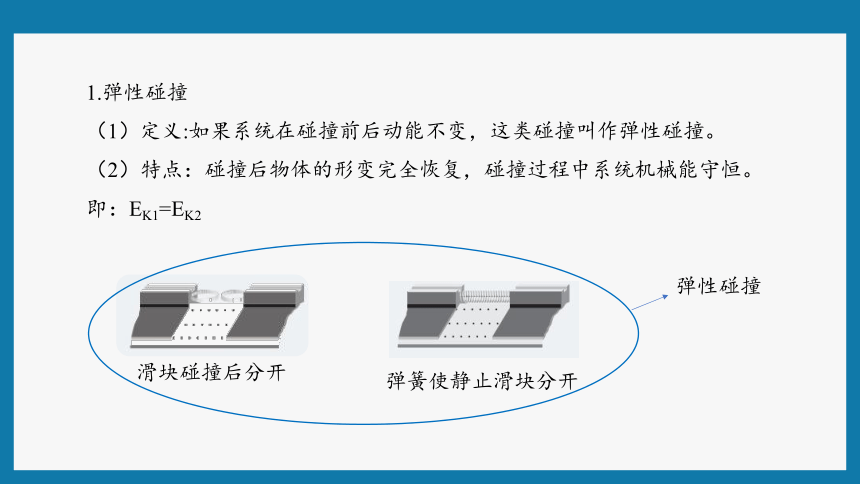
1.弹性碰撞
(1)定义:如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
(2)特点:碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
即:EK1=EK2
滑块碰撞后分开
弹簧使静止滑块分开
弹性碰撞
钢球、玻璃球碰撞时,机械能损失很小,它们的碰撞可以看作弹性碰撞。
2、非弹性碰撞:
(1)定义:如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
(2)特点:碰撞后不能完全恢复形变,碰撞过程中系统机械能减少。
即:EK1>EK2
3.完全非弹性碰撞
碰撞后两物体一起以同一速度运动,碰撞后物体的形变完全不能恢复,系统机械能损失最大。
种类
特点
弹性碰撞
动量守恒,机械能守恒
非弹性碰撞
动量守恒,机械能有损失
完全非弹性碰撞
动量守恒,机械能损失最大
思考:你能归纳总结碰撞的种类以及其特点吗?
例1.如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失?
m
解 :根据动量守恒定律, 2mv′= mv,则
v′= 1?2?v
碰撞前的总动能 E k =1?2? mv2
碰撞后的总动能 E k ′= 1?2?(2m)v′2= 1?2?E k
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
?
m
变式训练:现有甲、乙两滑块,质量分别为2m和m,以相同的速率v在光滑水平面上相向运动并发生碰撞。若碰撞后,甲滑块静止不动,则碰撞过程中损失的机械能为( )
A.1?6? mv2
B.1?4? mv2
C. 1?2? mv2
D. mv2
?
D
技法点拨:
可以先根据动量守恒定律求出碰撞后的乙的速度 v′,然后分别计算碰撞前后的总动能再进行相减即为碰撞过程中损失的机械能。
二、弹性碰撞的实例分析
1.正碰
碰撞前后,物体的运动方向在同一直线上。这种碰撞称为正碰,也叫作对心碰撞或一维碰撞。
碰撞前
碰撞后
2.斜碰(非对心碰撞)
碰撞前后物体的运动方向不在同一直线上,如图所示
碰撞前
碰撞后
碰撞前
碰撞后
3.弹性碰撞规律
例题:物体 m1 以速度 v1 与原来静止的物体 m2 发生正碰,如图所示。碰撞后它们的速度分别为v1′和 v2′。请分析发生弹性碰撞的两个物体,由于
质量不同,碰撞后的速度有哪些特点?
运动物体与静止物体碰撞
分析:碰撞过程遵从动量守恒定律,据此可以列出包含上述各已知量和未知量的方程:m1 v1 = m1 v1′+ m2 v2′ (1)
弹性碰撞中没有动能损失,于是可以列出另一个方程:
1?2?m1 v12 =1?2?m1 v1′2+1?2? m2 v2′2 (2)
从方程(1)(2)可以解出两个物体碰撞后的速度分别为:
?
v2′= (4)
v1′= (3)
我们对几种情况下(3)(4)的结果作一些分析。
①若 m1 = m2,可得v1′= 0 v2′= v1 相当于两球交换速度。
②若 m1 > m2 ,则v1′> 0 ,且v2′一定大于零。
若 m1 < m2 ,则v1′< 0 ,且v2′一定大于零。
③若 m1>>m2 ,这时有m1 - m2 ≈ m1 ,m1 + m2 ≈ m1。可得
v1′= v1 v2′= 2v1。
这表示碰撞后,第一个物体的速度几乎没有改变,而第二个物体以 2v1 的速度被撞出去.
保龄球比赛中,用大号保龄球击打球瓶时,球与瓶的碰撞就类似这种情况。
④若 m1<< m2,这时有m1 - m2 ≈ - m2,
可得:v1′=- v1 v2′= 0
≈ 0
这表示碰撞以后,第一个物体被弹了回去,以原来的速率向反方向运动,而第二个物体仍然静止。
如果用乒乓球撞击保龄球,那么就会出现这种现象:保龄球保持静止,而乒乓球以大致相同的速率被弹回。
例1.如图所示,物块A与轻质弹簧相连并静止在光滑水平面上,物块B以一定的初速度向物块A运动。在两物块与弹簧作用的过程中,两物块的V-t图像如图所示,则( )
A
A.物块A的质量大于物块 的质量
B.弹簧在t2时刻的弹性势能最大
C.物块A在t2时刻的加速度最大
D.物块B在0~t3时间内动能一直减小
变式训练:带有1?4? 光滑圆弧轨道、质量为m0的小车静止置于光滑水平面上,如图所示。一个质量为m的小球以速度v0 水平冲上小车,当小球上滑再返回,并脱离滑车时,以下说法正确的是( )
A.小球一定沿水平方向向左做平抛运动
B.小球一定沿水平方向向右做平抛运动
C.若m=1?3? m0 ,则小球沿水平方向向
左做平抛运动。
D.若小球初速度 v0足够大,以致小球能从滑道右端冲出小车,则小球再也落不进小车。
?
C
技法点拨:
ABC:根据球离开滑车的整个过程中,系统水平方向动量守恒。
mv0= m0v1+mv2由机械能守恒得:
解出v1和v2再进行讨论
再见
1. 了解弹性碰撞和非弹性碰撞。
2.会分析具体实例中的碰撞特点及类型。
3.知道对心碰撞和非对心碰撞,加深对动量守恒定律和机械能守恒定律的理解。
学习重点:掌握什么是弹性碰撞、非弹性碰撞和完全非弹性碰撞。
学习难点:分析具体实例、碰撞可能发生的判定
思考:碰撞是自然界中常见的现象,你能列举出一些碰撞现象吗?
汽车之间的碰撞
网球和球拍的碰撞
肢体之间的碰撞
陨石撞击地球
水上电动碰碰船
思考:那么如果从能量的角度去研究碰撞前后物体动能的变化,该如何对碰撞进行分类呢?
大部分物体碰撞的特点:
1.相互作用时间极短。
2.相互作用力极大,即内力远大于外力,遵循动量守恒定律。
一、弹性碰撞和非弹性碰撞
研究小车碰撞前后的动能变化
如图滑轨上有两辆安装了弹性碰撞架的小车,它们发生碰撞后改变了运动状态。测量两辆小车的质量以及它们碰撞前后的速度,研究碰撞前后总动能的变化情况。
研究两辆小车碰撞前后总动能的变化情况
碰撞前
碰撞后
质量
m1=0.10kg
m2=0.15kg
m1=0.10kg
m2=0.15kg
速度
V1=0.4m/s
V2=-0.2m/s
V1?=-0.32m/s
V2?=0.28m/s
12mv2
12m1v12+12m2v22=
12m1v1?2+12m2v2?2=
0.011J
0.011J
通过实验可以发现,在上述实验条件下,碰撞前后总动能基本不变。
1.弹性碰撞
(1)定义:如果系统在碰撞前后动能不变,这类碰撞叫作弹性碰撞。
(2)特点:碰撞后物体的形变完全恢复,碰撞过程中系统机械能守恒。
即:EK1=EK2
滑块碰撞后分开
弹簧使静止滑块分开
弹性碰撞
钢球、玻璃球碰撞时,机械能损失很小,它们的碰撞可以看作弹性碰撞。
2、非弹性碰撞:
(1)定义:如果系统在碰撞后动能减少,这类碰撞叫作非弹性碰撞。
(2)特点:碰撞后不能完全恢复形变,碰撞过程中系统机械能减少。
即:EK1>EK2
3.完全非弹性碰撞
碰撞后两物体一起以同一速度运动,碰撞后物体的形变完全不能恢复,系统机械能损失最大。
种类
特点
弹性碰撞
动量守恒,机械能守恒
非弹性碰撞
动量守恒,机械能有损失
完全非弹性碰撞
动量守恒,机械能损失最大
思考:你能归纳总结碰撞的种类以及其特点吗?
例1.如图,在光滑水平面上,两个物体的质量都是m,碰撞前一个物体静止,另一个以速度v 向它撞去。碰撞后两个物体粘在一起,成为一个质量为2m 的物体,以一定速度继续前进。碰撞后该系统的总动能是否会有损失?
m
解 :根据动量守恒定律, 2mv′= mv,则
v′= 1?2?v
碰撞前的总动能 E k =1?2? mv2
碰撞后的总动能 E k ′= 1?2?(2m)v′2= 1?2?E k
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
?
m
变式训练:现有甲、乙两滑块,质量分别为2m和m,以相同的速率v在光滑水平面上相向运动并发生碰撞。若碰撞后,甲滑块静止不动,则碰撞过程中损失的机械能为( )
A.1?6? mv2
B.1?4? mv2
C. 1?2? mv2
D. mv2
?
D
技法点拨:
可以先根据动量守恒定律求出碰撞后的乙的速度 v′,然后分别计算碰撞前后的总动能再进行相减即为碰撞过程中损失的机械能。
二、弹性碰撞的实例分析
1.正碰
碰撞前后,物体的运动方向在同一直线上。这种碰撞称为正碰,也叫作对心碰撞或一维碰撞。
碰撞前
碰撞后
2.斜碰(非对心碰撞)
碰撞前后物体的运动方向不在同一直线上,如图所示
碰撞前
碰撞后
碰撞前
碰撞后
3.弹性碰撞规律
例题:物体 m1 以速度 v1 与原来静止的物体 m2 发生正碰,如图所示。碰撞后它们的速度分别为v1′和 v2′。请分析发生弹性碰撞的两个物体,由于
质量不同,碰撞后的速度有哪些特点?
运动物体与静止物体碰撞
分析:碰撞过程遵从动量守恒定律,据此可以列出包含上述各已知量和未知量的方程:m1 v1 = m1 v1′+ m2 v2′ (1)
弹性碰撞中没有动能损失,于是可以列出另一个方程:
1?2?m1 v12 =1?2?m1 v1′2+1?2? m2 v2′2 (2)
从方程(1)(2)可以解出两个物体碰撞后的速度分别为:
?
v2′= (4)
v1′= (3)
我们对几种情况下(3)(4)的结果作一些分析。
①若 m1 = m2,可得v1′= 0 v2′= v1 相当于两球交换速度。
②若 m1 > m2 ,则v1′> 0 ,且v2′一定大于零。
若 m1 < m2 ,则v1′< 0 ,且v2′一定大于零。
③若 m1>>m2 ,这时有m1 - m2 ≈ m1 ,m1 + m2 ≈ m1。可得
v1′= v1 v2′= 2v1。
这表示碰撞后,第一个物体的速度几乎没有改变,而第二个物体以 2v1 的速度被撞出去.
保龄球比赛中,用大号保龄球击打球瓶时,球与瓶的碰撞就类似这种情况。
④若 m1<< m2,这时有m1 - m2 ≈ - m2,
可得:v1′=- v1 v2′= 0
≈ 0
这表示碰撞以后,第一个物体被弹了回去,以原来的速率向反方向运动,而第二个物体仍然静止。
如果用乒乓球撞击保龄球,那么就会出现这种现象:保龄球保持静止,而乒乓球以大致相同的速率被弹回。
例1.如图所示,物块A与轻质弹簧相连并静止在光滑水平面上,物块B以一定的初速度向物块A运动。在两物块与弹簧作用的过程中,两物块的V-t图像如图所示,则( )
A
A.物块A的质量大于物块 的质量
B.弹簧在t2时刻的弹性势能最大
C.物块A在t2时刻的加速度最大
D.物块B在0~t3时间内动能一直减小
变式训练:带有1?4? 光滑圆弧轨道、质量为m0的小车静止置于光滑水平面上,如图所示。一个质量为m的小球以速度v0 水平冲上小车,当小球上滑再返回,并脱离滑车时,以下说法正确的是( )
A.小球一定沿水平方向向左做平抛运动
B.小球一定沿水平方向向右做平抛运动
C.若m=1?3? m0 ,则小球沿水平方向向
左做平抛运动。
D.若小球初速度 v0足够大,以致小球能从滑道右端冲出小车,则小球再也落不进小车。
?
C
技法点拨:
ABC:根据球离开滑车的整个过程中,系统水平方向动量守恒。
mv0= m0v1+mv2由机械能守恒得:
解出v1和v2再进行讨论
再见
