2.5实验:用单摆测量重力加速度 课件(26张PPT)
文档属性
| 名称 | 2.5实验:用单摆测量重力加速度 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-12 00:00:00 | ||
图片预览








文档简介
2.5 实验:用单摆测量重力加速度
思考:当摆角较小时,单摆做简谐运动,你能根据单摆的周期公式T=2????Lg测量g吗?
?
理论上,与重力相关的物理现象都可以用来测量g。例如,利用自由落体运动就可以测量g。
实验:用单摆测量重力加速度
1.实验思路
单摆做简谐运动时,其周期为: T=2????Lg??得
只要测出单摆的摆长L和振动周期T,就可以求出当地的重力加速度g的值。
(1)测量摆长需要刻度尺
(2)测量周期需要秒表
?
思考:应该如何设计实验装置、选择实验器材?怎样才能减小实验误差?
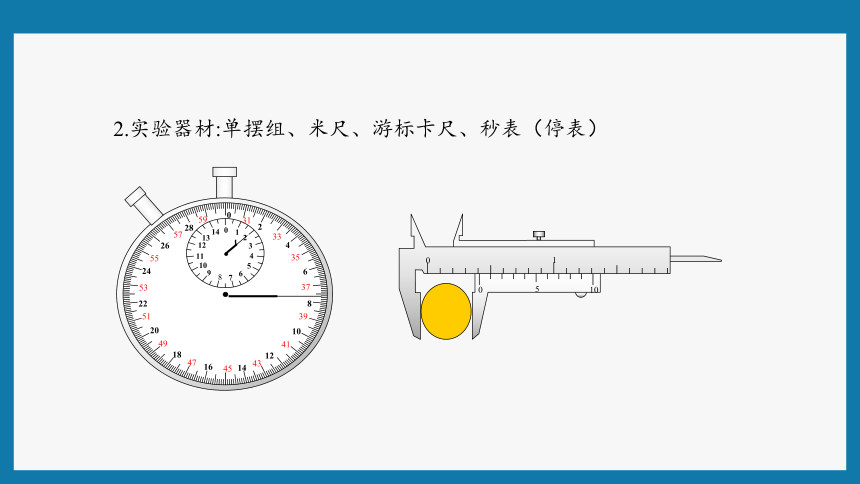
2.实验器材:单摆组、米尺、游标卡尺、秒表(停表)
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
0
5
10
0
1
(1)做单摆
①让线的一端穿过小球的小孔,然后打一个比小孔大一些的结。
②把线的上端用铁夹固定在铁架台上并把铁架台放在实验桌边,使铁夹伸到桌面以外,让摆球自由下垂,在单摆平衡位置处作上标记。
3.实验装置
特别提醒
线:选用一米左右不可伸长的细线;
球:选用中心有小孔的金属小球;
表:应选用停表;
尺:测绳的长度用米尺,测小球直径用游标卡尺。
思考讨论1
线有粗细、长短的不同,伸缩性也有区别。不同的小球,质量和体积有差异。想一想,应如何选择摆线和摆球?为什么?
参考答案:线要细、轻、不易伸长,摆球要体积小、质量大(密度大)。
线要细、轻、不易伸长,这样线的质量与小球相比可以忽略,且体积小空气阻力小,细线不易伸长这样摆长测量准确。这样就减小了系统误差和偶然误差。
思考讨论2
图中画出了细线上端的两种不同的悬挂方式。应该选用哪种方式?为什么?
甲
乙
应该选用乙,这样摆长一定,实验更准确。甲图悬点不固定,可能会出现摆动时发生摆线下滑或悬点不固定,摆长改变的现象。
4.物理量的测量
(1)摆长的测量
方法一:用刻度尺直接侧量小球球心与悬挂点之间的距离作为摆长l。
方法二:用刻度尺先测量悬挂点与小球上端之间的距离l1,再测量悬挂点与小球下端之间的距离l2,则可得摆长l=( l1+l2)/2
方法三
①用米尺量出悬线长L,准确到毫米
②用游标卡尺测摆球直径
算出半径r,也准确到毫米
③摆长:l=l′+d2。
?
0
5
10
0
1
(2)测周期
用停表测量单摆的周期。
方法①:测量单摆做一次全振动的时间作为它的周期的测值。
方法②:测量单摆做多次全振动(例如几十次)的时间,然后通过计算求出它
的周期的测量值.
思考:以上用停表测量单摆的周期,哪种方法比较好?为什么?
方法②可以减少停表的测量误差,是最优方法。
思考:为了测量周期,摆球到达哪个位置的时刻作为计时开始与停止的时刻比较好?
参考答案:到达最高点的位置不容易判断,在最低点容易判断,所以应以摆球经平衡位置计时开始与停止时刻。
5.数据处理
(1)平均值法:改变摆长,重做几次实验。从测量的数据中选择几组,根据前面推导的公式,分别计算重力加速度,然后取平均值作为测量结果。
T=2????Lg??得
?
多组数据代入,取平均值
思考:除了这种方法,你还能想出别的方法来处理实验数据,得到重力加速度吗?
还可以用图象法:分别以l和T2为横坐标和纵坐标,作出l=g4π2 T2 的图象,它应该是过原点的一条直线,根据这条直线可以求出斜率k,则重力加速度值g=4π2?k。
即: l=g4π2 T2
?
由l- T2图象求出斜率k=g4π2
?
g=4π2?k
?
1.0
4
3
2
0.8
0.5
0
l/m
T2/s2
6.注意事项
(1)选择材料时应选择细轻又不易伸长的线,长度一般在1m左右,小球应选用密度较大的金属球,直径应较小。
(2)单摆摆球应在坚直平面内摆动,且摆角应小于5°以保证单摆做简谐运动。
(3)计算单摆的振动次数时,应从小球通过最低位置(平衡位置)时开始计时,同方向再次通过最低位置时累加计数,适当增加全振动的测量次数,以减小测量周期的误差,一般30~50次即可。
(4)测量摆长时应注意是悬点到球心的距离,等于摆线长加上小球半径。
(1)系统误差:主要来源于单摆模型本身是否符合要求,即悬点是否固定,球和线是否符合要求,振动是圆锥摆还是在同一竖直面内的振动。
(2)偶然误差:主要来自时间的测量上。因此,要从摆球通过平衡位置开始计时,不能多计或漏计振动次数。
(3)减小偶然误差通常采用两种方法
①多次测量求平均值法;
②图像法。
7.误差分析
例1.某研究性学习小组在进行“用单摆测定重力加速度”的实验中(实验装置如图所示),已知单摆在摆动过程中的最大偏角小 。
(1)安装好实验装置后,先用游标卡尺测量摆球直径d,测量的示数如图所示,则摆球直径d= _______ cm,再测量摆线长l,则单摆摆长 L=___________(用d、l表示);
1.87
l +d2
?
(2)摆球摆动稳定后,当它到达最低点时启动秒表开始计时,并记录此后摆球再次经过最低点的次数n (n=1、2、3······ ),当n=60 时刚好停表.停止计时的秒表读数为67.5 ,该单摆的周期为T= ______s(周期要求保留三位有效数字);
(3)计算重力加速度测量值的表达式为g= _______(用T、L表示),如果测量值小于真实值,可能原因是__________;
A.将摆球经过最低点的次数n计少了
B.计时开始时,秒表启动稍晚
C.将摆线长当成了摆长
D.将摆线长和球的直径之和当成了摆长
2.25
4π2????T2
?
AC
(4)正确测量不同摆长L及相应的单摆周期T,并在坐标纸上画出T2与L的关系图线,如图所示
由图线算出重力加速度的大小 _____ m/s2(保留3位有效数字,计算时π2取9.86)。
9.86
【详解】
(1)[1] 摆球直径为d=1.8cm+7×0.01cm=1.87cm
[2] 单摆摆长从悬点到小球球心间的距离,即: L=l +d2
(2)[3]由题意可知T=????????2=67.530=2.25s
(3)[4]根据周期公式得g=4????2????????2
[5]周期公式为g=4????2????????2=????2????2(????+?????2)????2
?
测量结果偏小,则可能的原因是将摆球经过最低点的次数n计少了、将摆线长当成了摆长、秒表启动稍早,故选AC。
(4)[6]图像的斜率为
解得g=9.8m/s2
变式训练:某同学利用单摆测当地重力加速度:
(1)用游标卡尺测得金属小球直径如图所示,小球直径d=_________cm;
(2)该组同学先测出悬点到小球球心的距离L,然后用秒表测出单摆完成n次全振动所用的时间t。请写出重力加速度的表达式g=________。(用所测物理量表示)
(3)在测量摆长后,测量周期时,摆球振动过程中悬点O处摆线的固定出现松动,摆长略微变长,这将会导致所测重力加速度的数值__________。(选填“偏大”、“偏小”或“不变”)
2.26
偏小
(4)某同学利用测出的多组摆长l和周期T的值,作出T2-l图线如图所示,通过测量计算出图线的斜率为k,由斜率k求重力加速度的表达式是g=_______;
技法点拨:
(1)游标卡尺的读数读主尺的整敬部分、游标尺的小数部分。
(2)根据单摆的周期公式 T=2???? ???????? 以及T=????????推导出重力加速度的表达式
?
(3)由题意知,摆长的测量值比实际偏小,根据
可判断g的变化
(4)根据单摆的周期公式 T=2???? ???????? 推导出T2-l的关系。
?
实验:用单摆测量重力加速度
实验思路:当摆角较小时,单摆做简谐运动,根据其周期公式可得:g=4????2????????2
?
数据分析
实验装置
物理量的测量
周期的测量:T=????????
?
摆长的测量:L=l+????2
?
再见
思考:当摆角较小时,单摆做简谐运动,你能根据单摆的周期公式T=2????Lg测量g吗?
?
理论上,与重力相关的物理现象都可以用来测量g。例如,利用自由落体运动就可以测量g。
实验:用单摆测量重力加速度
1.实验思路
单摆做简谐运动时,其周期为: T=2????Lg??得
只要测出单摆的摆长L和振动周期T,就可以求出当地的重力加速度g的值。
(1)测量摆长需要刻度尺
(2)测量周期需要秒表
?
思考:应该如何设计实验装置、选择实验器材?怎样才能减小实验误差?
2.实验器材:单摆组、米尺、游标卡尺、秒表(停表)
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
0
5
10
0
1
(1)做单摆
①让线的一端穿过小球的小孔,然后打一个比小孔大一些的结。
②把线的上端用铁夹固定在铁架台上并把铁架台放在实验桌边,使铁夹伸到桌面以外,让摆球自由下垂,在单摆平衡位置处作上标记。
3.实验装置
特别提醒
线:选用一米左右不可伸长的细线;
球:选用中心有小孔的金属小球;
表:应选用停表;
尺:测绳的长度用米尺,测小球直径用游标卡尺。
思考讨论1
线有粗细、长短的不同,伸缩性也有区别。不同的小球,质量和体积有差异。想一想,应如何选择摆线和摆球?为什么?
参考答案:线要细、轻、不易伸长,摆球要体积小、质量大(密度大)。
线要细、轻、不易伸长,这样线的质量与小球相比可以忽略,且体积小空气阻力小,细线不易伸长这样摆长测量准确。这样就减小了系统误差和偶然误差。
思考讨论2
图中画出了细线上端的两种不同的悬挂方式。应该选用哪种方式?为什么?
甲
乙
应该选用乙,这样摆长一定,实验更准确。甲图悬点不固定,可能会出现摆动时发生摆线下滑或悬点不固定,摆长改变的现象。
4.物理量的测量
(1)摆长的测量
方法一:用刻度尺直接侧量小球球心与悬挂点之间的距离作为摆长l。
方法二:用刻度尺先测量悬挂点与小球上端之间的距离l1,再测量悬挂点与小球下端之间的距离l2,则可得摆长l=( l1+l2)/2
方法三
①用米尺量出悬线长L,准确到毫米
②用游标卡尺测摆球直径
算出半径r,也准确到毫米
③摆长:l=l′+d2。
?
0
5
10
0
1
(2)测周期
用停表测量单摆的周期。
方法①:测量单摆做一次全振动的时间作为它的周期的测值。
方法②:测量单摆做多次全振动(例如几十次)的时间,然后通过计算求出它
的周期的测量值.
思考:以上用停表测量单摆的周期,哪种方法比较好?为什么?
方法②可以减少停表的测量误差,是最优方法。
思考:为了测量周期,摆球到达哪个位置的时刻作为计时开始与停止的时刻比较好?
参考答案:到达最高点的位置不容易判断,在最低点容易判断,所以应以摆球经平衡位置计时开始与停止时刻。
5.数据处理
(1)平均值法:改变摆长,重做几次实验。从测量的数据中选择几组,根据前面推导的公式,分别计算重力加速度,然后取平均值作为测量结果。
T=2????Lg??得
?
多组数据代入,取平均值
思考:除了这种方法,你还能想出别的方法来处理实验数据,得到重力加速度吗?
还可以用图象法:分别以l和T2为横坐标和纵坐标,作出l=g4π2 T2 的图象,它应该是过原点的一条直线,根据这条直线可以求出斜率k,则重力加速度值g=4π2?k。
即: l=g4π2 T2
?
由l- T2图象求出斜率k=g4π2
?
g=4π2?k
?
1.0
4
3
2
0.8
0.5
0
l/m
T2/s2
6.注意事项
(1)选择材料时应选择细轻又不易伸长的线,长度一般在1m左右,小球应选用密度较大的金属球,直径应较小。
(2)单摆摆球应在坚直平面内摆动,且摆角应小于5°以保证单摆做简谐运动。
(3)计算单摆的振动次数时,应从小球通过最低位置(平衡位置)时开始计时,同方向再次通过最低位置时累加计数,适当增加全振动的测量次数,以减小测量周期的误差,一般30~50次即可。
(4)测量摆长时应注意是悬点到球心的距离,等于摆线长加上小球半径。
(1)系统误差:主要来源于单摆模型本身是否符合要求,即悬点是否固定,球和线是否符合要求,振动是圆锥摆还是在同一竖直面内的振动。
(2)偶然误差:主要来自时间的测量上。因此,要从摆球通过平衡位置开始计时,不能多计或漏计振动次数。
(3)减小偶然误差通常采用两种方法
①多次测量求平均值法;
②图像法。
7.误差分析
例1.某研究性学习小组在进行“用单摆测定重力加速度”的实验中(实验装置如图所示),已知单摆在摆动过程中的最大偏角小 。
(1)安装好实验装置后,先用游标卡尺测量摆球直径d,测量的示数如图所示,则摆球直径d= _______ cm,再测量摆线长l,则单摆摆长 L=___________(用d、l表示);
1.87
l +d2
?
(2)摆球摆动稳定后,当它到达最低点时启动秒表开始计时,并记录此后摆球再次经过最低点的次数n (n=1、2、3······ ),当n=60 时刚好停表.停止计时的秒表读数为67.5 ,该单摆的周期为T= ______s(周期要求保留三位有效数字);
(3)计算重力加速度测量值的表达式为g= _______(用T、L表示),如果测量值小于真实值,可能原因是__________;
A.将摆球经过最低点的次数n计少了
B.计时开始时,秒表启动稍晚
C.将摆线长当成了摆长
D.将摆线长和球的直径之和当成了摆长
2.25
4π2????T2
?
AC
(4)正确测量不同摆长L及相应的单摆周期T,并在坐标纸上画出T2与L的关系图线,如图所示
由图线算出重力加速度的大小 _____ m/s2(保留3位有效数字,计算时π2取9.86)。
9.86
【详解】
(1)[1] 摆球直径为d=1.8cm+7×0.01cm=1.87cm
[2] 单摆摆长从悬点到小球球心间的距离,即: L=l +d2
(2)[3]由题意可知T=????????2=67.530=2.25s
(3)[4]根据周期公式得g=4????2????????2
[5]周期公式为g=4????2????????2=????2????2(????+?????2)????2
?
测量结果偏小,则可能的原因是将摆球经过最低点的次数n计少了、将摆线长当成了摆长、秒表启动稍早,故选AC。
(4)[6]图像的斜率为
解得g=9.8m/s2
变式训练:某同学利用单摆测当地重力加速度:
(1)用游标卡尺测得金属小球直径如图所示,小球直径d=_________cm;
(2)该组同学先测出悬点到小球球心的距离L,然后用秒表测出单摆完成n次全振动所用的时间t。请写出重力加速度的表达式g=________。(用所测物理量表示)
(3)在测量摆长后,测量周期时,摆球振动过程中悬点O处摆线的固定出现松动,摆长略微变长,这将会导致所测重力加速度的数值__________。(选填“偏大”、“偏小”或“不变”)
2.26
偏小
(4)某同学利用测出的多组摆长l和周期T的值,作出T2-l图线如图所示,通过测量计算出图线的斜率为k,由斜率k求重力加速度的表达式是g=_______;
技法点拨:
(1)游标卡尺的读数读主尺的整敬部分、游标尺的小数部分。
(2)根据单摆的周期公式 T=2???? ???????? 以及T=????????推导出重力加速度的表达式
?
(3)由题意知,摆长的测量值比实际偏小,根据
可判断g的变化
(4)根据单摆的周期公式 T=2???? ???????? 推导出T2-l的关系。
?
实验:用单摆测量重力加速度
实验思路:当摆角较小时,单摆做简谐运动,根据其周期公式可得:g=4????2????????2
?
数据分析
实验装置
物理量的测量
周期的测量:T=????????
?
摆长的测量:L=l+????2
?
再见
