2.5 解直角三角形的应用 课时练习 2021-2022学年青岛版数学九年级上册(Word版含答案)
文档属性
| 名称 | 2.5 解直角三角形的应用 课时练习 2021-2022学年青岛版数学九年级上册(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 217.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 18:05:28 | ||
图片预览



文档简介
青岛版数学九年级上册
2.5《解直角三角形的应用》课时练习
一、选择题
1.某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, =1.732).
A.585米 B.1014米 C.805米 D.820米
2.如图,某建筑物CE上挂着“巴山渝水,魅力重庆”的宣传条幅CD,王同学利用测倾器在斜坡的底部A处测得条幅底部D的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°,已知斜坡AB的坡度i=1:2.4,AB=13米,AE=12米(点A、B、C、D、E在同一平面内,CD⊥AE,测倾器的高度忽略不计),则条幅CD的长度约为(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,≈1.73)( )
A.12.5米 B.12.8米 C.13.1米 D.13.4米
3.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
A.26米 B.28米 C.30米 D.46米
4.一座楼梯的示意图如图,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2 B.米2 C.(4+)米2 D.(4+4tanθ)米2
5.数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE 的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为ɑ,已知sinɑ=0.6,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.
A.7.4 B.7.2 C.7 D.6.8
6.在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A. B. C. D.
7.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB为( )
A.50米 B.51米 C.(50+1)米 D.101米
8.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为( )
(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.65.8米 B.71.8米 C.73.8米 D.119.8米
9.“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地跑到D地的路程是( )
A.30m B.20m C.30m D.15m
10.如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )
A.20(+1)米/秒 B.20(-1)米/秒 C.200米/秒 D.300米/秒
二、填空题
11.某同学沿坡比为1:的斜坡前进了90米,那么他上升的高度是 米.
12.如图,一水库迎水坡AB的坡度︰,则该坡的坡角= .
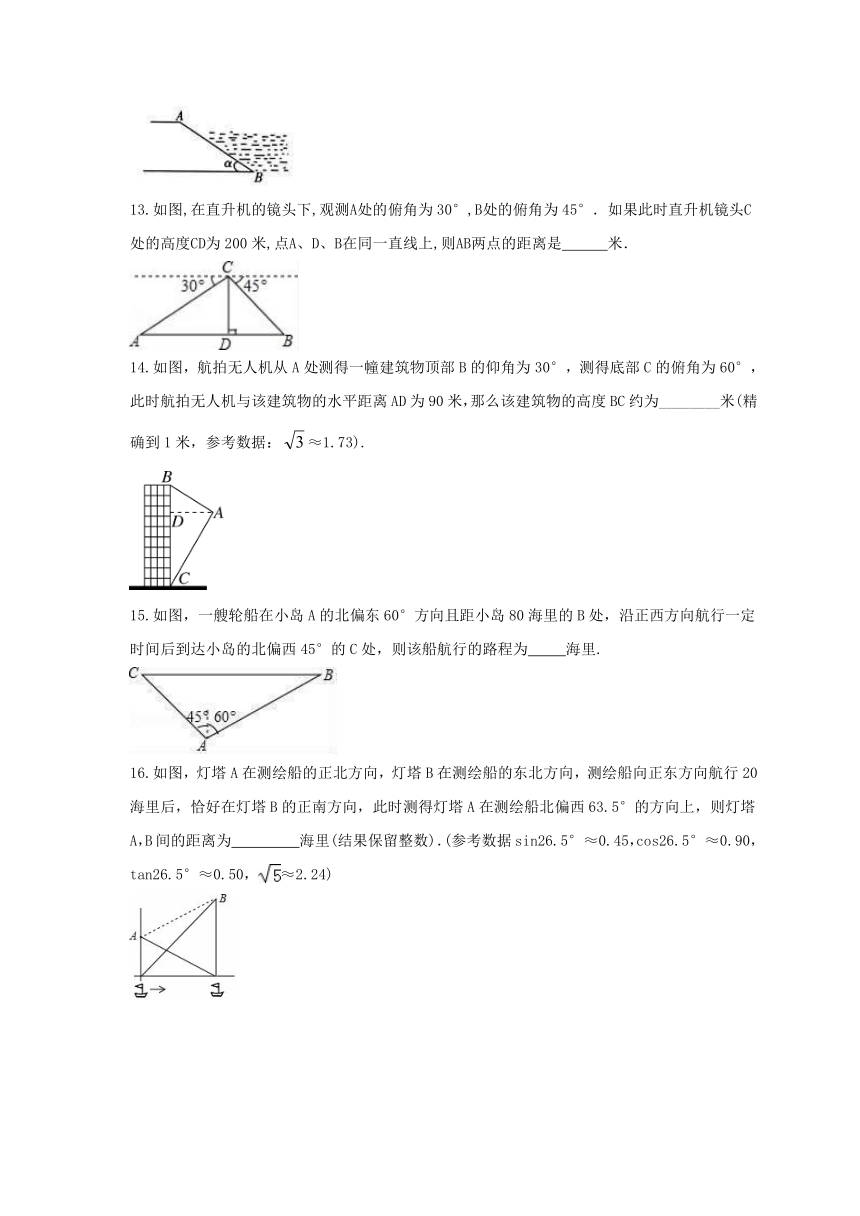
13.如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是 米.
14.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为________米(精确到1米,参考数据:≈1.73).
15.如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为 海里.
16.如图,灯塔A在测绘船的正北方向,灯塔B在测绘船的东北方向,测绘船向正东方向航行20海里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘船北偏西63.5°的方向上,则灯塔A,B间的距离为 ?? 海里(结果保留整数).(参考数据sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50,≈2.24)
三、解答题
17.如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20m,点C与点A在同一水平线上,A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)
18.如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据:,
19.如图,在河对岸有一棵大树A,在河岸B点测得A在北偏东60°方向上,向东前进120m到达C点,测得A在北偏东30°方向上,求河的宽度(精确到0.1m)参考数据:=1.414,=1.732
20.由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.
参考答案
1.C;
2.B;
3.D
4.D
5.D
6.D.
7.C
8.B;
9.D.
10.A.
11.答案为:45.
12.答案为:30°
13.答案为200()米.
14.答案为:208.
15.答案为:(40+40)海里.
16.答案为:22.4.
17.解:(1)过点C作CE⊥BP于点E,
在Rt△CPE中,∵PC=20m,∠CPE=45°,
∴sin45°=,∴CE=PC?sin45°=20×=20m,
∵点C与点A在同一水平线上,∴AB=CE=20m,
答:居民楼AB的高度约为20m;
(2)在Rt△ABP中,∵∠APB=60°,∴tan60°=,∴BP==m,
∵PE=CE=20m,∴AC=BE=(+20)m,
答:C、A之间的距离为(+20)m.
18.解:
19.解:如图,过点A作AD⊥BC于点D,
设河宽AD的长为x,
∵在河岸B点测得A在北偏东60°方向上,向东前进120m到达C点,
测得A在北偏东30°方向,∴∠BAD=60°,∠CAD=30°,BC=120,
在Rt△ADB中,BD=tan∠BAD×AD=tan60°x=x,
在Rt△ACD中,CD=tan∠CAD×AD=tan30°x=x,
∵BC=BD﹣CD,∴x﹣x=120,
解得x=60≈60×1.732≈103.9(m),
答:河宽为103.9米.
20.解:过点C作CD⊥AB于点D,
由题意,得:∠BAD=60°,∠BCD=45°,AC=80,
在Rt△ADB中,∠BAD=60°,∴tan60°==,∴AD=,
在Rt△BCD中,∠BCD=45°,∴tan45°==1,∴BD=CD,
∴AC=AD+CD=+BD=80,∴BD=120﹣40,
∴BC=BC=120﹣40,
答:BC的距离是(120﹣40)海里.
2.5《解直角三角形的应用》课时练习
一、选择题
1.某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, =1.732).
A.585米 B.1014米 C.805米 D.820米
2.如图,某建筑物CE上挂着“巴山渝水,魅力重庆”的宣传条幅CD,王同学利用测倾器在斜坡的底部A处测得条幅底部D的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°,已知斜坡AB的坡度i=1:2.4,AB=13米,AE=12米(点A、B、C、D、E在同一平面内,CD⊥AE,测倾器的高度忽略不计),则条幅CD的长度约为(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,≈1.73)( )
A.12.5米 B.12.8米 C.13.1米 D.13.4米
3.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
A.26米 B.28米 C.30米 D.46米
4.一座楼梯的示意图如图,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2 B.米2 C.(4+)米2 D.(4+4tanθ)米2
5.数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE 的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为ɑ,已知sinɑ=0.6,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.
A.7.4 B.7.2 C.7 D.6.8
6.在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A. B. C. D.
7.如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB为( )
A.50米 B.51米 C.(50+1)米 D.101米
8.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为( )
(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.65.8米 B.71.8米 C.73.8米 D.119.8米
9.“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地跑到D地的路程是( )
A.30m B.20m C.30m D.15m
10.如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )
A.20(+1)米/秒 B.20(-1)米/秒 C.200米/秒 D.300米/秒
二、填空题
11.某同学沿坡比为1:的斜坡前进了90米,那么他上升的高度是 米.
12.如图,一水库迎水坡AB的坡度︰,则该坡的坡角= .
13.如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是 米.
14.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为________米(精确到1米,参考数据:≈1.73).
15.如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为 海里.
16.如图,灯塔A在测绘船的正北方向,灯塔B在测绘船的东北方向,测绘船向正东方向航行20海里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘船北偏西63.5°的方向上,则灯塔A,B间的距离为 ?? 海里(结果保留整数).(参考数据sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50,≈2.24)
三、解答题
17.如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20m,点C与点A在同一水平线上,A、B、P、C在同一平面内.
(1)求居民楼AB的高度;
(2)求C、A之间的距离.(结果保留根号)
18.如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据:,
19.如图,在河对岸有一棵大树A,在河岸B点测得A在北偏东60°方向上,向东前进120m到达C点,测得A在北偏东30°方向上,求河的宽度(精确到0.1m)参考数据:=1.414,=1.732
20.由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达A处时,测得小岛B位于它的北偏东30°方向,且与航母相距80海里再航行一段时间后到达C处,测得小岛B位于它的西北方向,求此时航母与小岛的距离BC的长.
参考答案
1.C;
2.B;
3.D
4.D
5.D
6.D.
7.C
8.B;
9.D.
10.A.
11.答案为:45.
12.答案为:30°
13.答案为200()米.
14.答案为:208.
15.答案为:(40+40)海里.
16.答案为:22.4.
17.解:(1)过点C作CE⊥BP于点E,
在Rt△CPE中,∵PC=20m,∠CPE=45°,
∴sin45°=,∴CE=PC?sin45°=20×=20m,
∵点C与点A在同一水平线上,∴AB=CE=20m,
答:居民楼AB的高度约为20m;
(2)在Rt△ABP中,∵∠APB=60°,∴tan60°=,∴BP==m,
∵PE=CE=20m,∴AC=BE=(+20)m,
答:C、A之间的距离为(+20)m.
18.解:
19.解:如图,过点A作AD⊥BC于点D,
设河宽AD的长为x,
∵在河岸B点测得A在北偏东60°方向上,向东前进120m到达C点,
测得A在北偏东30°方向,∴∠BAD=60°,∠CAD=30°,BC=120,
在Rt△ADB中,BD=tan∠BAD×AD=tan60°x=x,
在Rt△ACD中,CD=tan∠CAD×AD=tan30°x=x,
∵BC=BD﹣CD,∴x﹣x=120,
解得x=60≈60×1.732≈103.9(m),
答:河宽为103.9米.
20.解:过点C作CD⊥AB于点D,
由题意,得:∠BAD=60°,∠BCD=45°,AC=80,
在Rt△ADB中,∠BAD=60°,∴tan60°==,∴AD=,
在Rt△BCD中,∠BCD=45°,∴tan45°==1,∴BD=CD,
∴AC=AD+CD=+BD=80,∴BD=120﹣40,
∴BC=BC=120﹣40,
答:BC的距离是(120﹣40)海里.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
