3.6《弧长及扇形面积的计算》课时练习(含答案) 2021--2022学年青岛版数学九年级上册
文档属性
| 名称 | 3.6《弧长及扇形面积的计算》课时练习(含答案) 2021--2022学年青岛版数学九年级上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 140.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览


文档简介
青岛版数学九年级上册
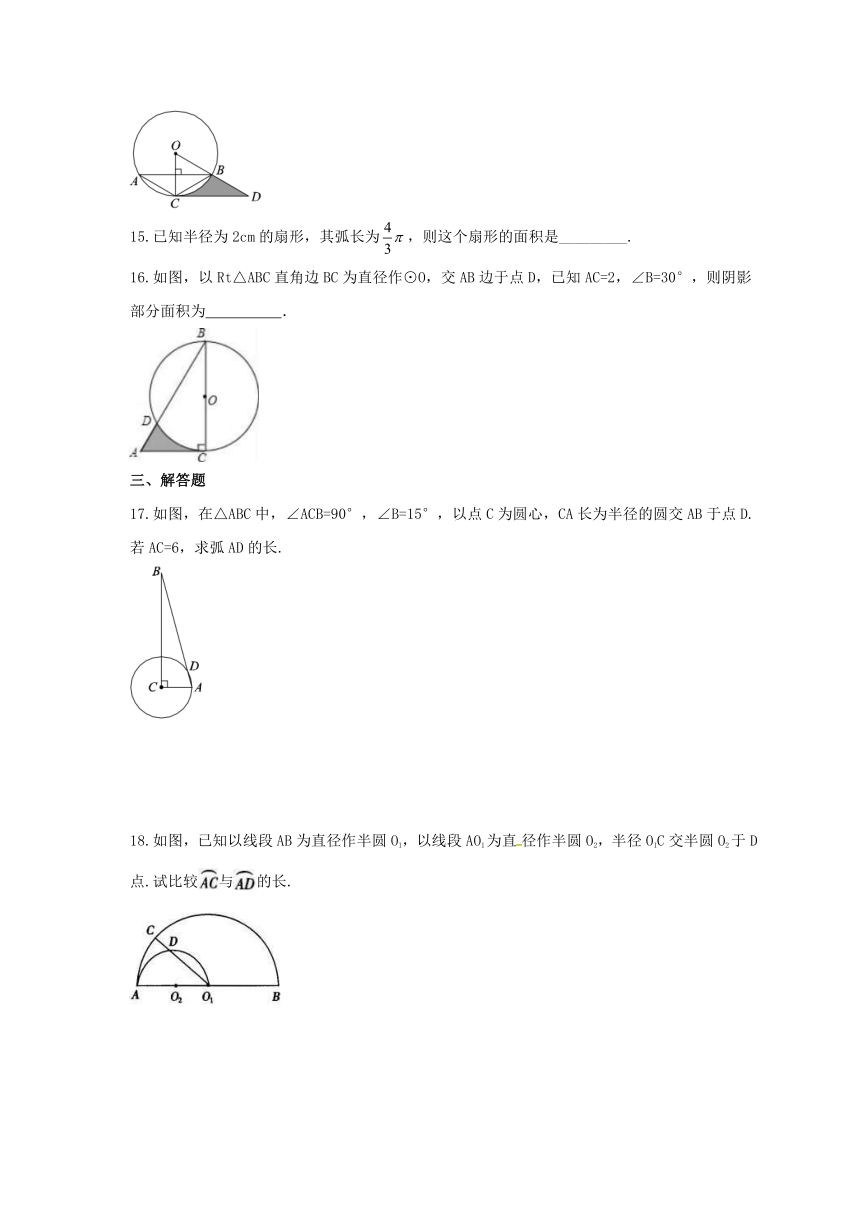
3.6《弧长及扇形面积的计算》课时练习
一、选择题
1.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
2.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π??? ?? B.2π???? ? C.2π??? ?? D.4π
3.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )
A.5πcm B.6πcm C.9πcm D.8πcm
4.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点 C.甲、乙同时到B D.无法确定
5.若120°的圆心角所对的弧长是6π,则此弧所在圆的半径是( )
A.3 B.4 C.9 D.18
6.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π?? ? B.2π?? ??? C.3π?? ?? D.6π
7.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π B.π C. D.
8.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A.cm B.cm C.cm D.cm
9.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是( ).
A.R=2r B. C.R=3r D.R=4r
10.如图,在4×4的正方形网格中,每个小正方形的边长都为1,△AOB的三个顶点都在格点上,现将△AOB绕点O逆时针旋转90°后得到对应的△COD,则点A经过的路径弧AC的长为( )
A.1.5π????? B.πp??? C.2π??? D.3π
二、填空题
11.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是 度.
12.已知扇形的弧长为4π,半径为8,则此扇形的圆心角为________.
13.若扇形的半径为3 cm,弧长为2π cm,则该扇形的面积为________ cm2.
14.如图,已知△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由弧BC、线段CD和线段BD所围成的阴影部分的面积为________.
15.已知半径为2cm的扇形,其弧长为,则这个扇形的面积是_________.
16.如图,以Rt△ABC直角边BC为直径作⊙O,交AB边于点D,已知AC=2,∠B=30°,则阴影部分面积为 .
三、解答题
17.如图,在△ABC中,∠ACB=90°,∠B=15°,以点C为圆心,CA长为半径的圆交AB于点D.若AC=6,求弧AD的长.
18.如图,已知以线段AB为直径作半圆O1,以线段AO1为直径作半圆O2,半径O1C交半圆O2于D点.试比较与的长.
19.如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠CAE=∠B=60°.
(1)求∠ADC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
20.如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°.
(1)求证:直线AD是⊙O的切线;
(2)若直径BC=4,求图中阴影部分的面积.
参考答案
1.答案为:C;
2.答案为:B.
3.答案为:D
4.答案为:C
5.答案为:C
6.答案为:C.
7.答案为:B.
8.答案为:B
9.答案为:D
10.答案为:A
11.答案为:110.
12.答案为:90°.
13.答案为:3π
14.答案为:2 -
15.答案为:cm2
16.答案为:﹣.
17.解:连接CD.
∵AC=CD,∴∠CAD=∠CDA.
∵∠ACB=90°,∠B=15°,∴∠CAD=75°,
∴∠ACD=30°.
∵AC=6,∴的长度为=π.
18.解:的长等于的长.
19.解:
(1)∵∠ABC与∠ADC都是弧AC所对的圆周角,
∴∠ADC=∠B=60°.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=30°.
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即?BA⊥AE.
∴AE是⊙O的切线.
(3)略.
20.解:(1)证明:连接OA,则∠COA=2∠B,
∵AD=AB,
∴∠B=∠D=30°,
∴∠COA=60°,
∴∠OAD=180°﹣60°﹣30°=90°,
∴OA⊥AD,
即CD是⊙O的切线;
(2)解:∵BC=4,∴OA=OC=2,
在Rt△OAD中,OA=2,∠D=30°,
∴OD=2OA=4,AD=2,所以S△OAD=OA?AD=×2×2=2,
因为∠COA=60°,所以S扇形COA==π,
所以S阴影=S△OAD﹣S扇形COA=2﹣.
3.6《弧长及扇形面积的计算》课时练习
一、选择题
1.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
2.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π??? ?? B.2π???? ? C.2π??? ?? D.4π
3.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )
A.5πcm B.6πcm C.9πcm D.8πcm
4.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点 C.甲、乙同时到B D.无法确定
5.若120°的圆心角所对的弧长是6π,则此弧所在圆的半径是( )
A.3 B.4 C.9 D.18
6.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π?? ? B.2π?? ??? C.3π?? ?? D.6π
7.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π B.π C. D.
8.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A.cm B.cm C.cm D.cm
9.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则R与r之间的关系是( ).
A.R=2r B. C.R=3r D.R=4r
10.如图,在4×4的正方形网格中,每个小正方形的边长都为1,△AOB的三个顶点都在格点上,现将△AOB绕点O逆时针旋转90°后得到对应的△COD,则点A经过的路径弧AC的长为( )
A.1.5π????? B.πp??? C.2π??? D.3π
二、填空题
11.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是 度.
12.已知扇形的弧长为4π,半径为8,则此扇形的圆心角为________.
13.若扇形的半径为3 cm,弧长为2π cm,则该扇形的面积为________ cm2.
14.如图,已知△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由弧BC、线段CD和线段BD所围成的阴影部分的面积为________.
15.已知半径为2cm的扇形,其弧长为,则这个扇形的面积是_________.
16.如图,以Rt△ABC直角边BC为直径作⊙O,交AB边于点D,已知AC=2,∠B=30°,则阴影部分面积为 .
三、解答题
17.如图,在△ABC中,∠ACB=90°,∠B=15°,以点C为圆心,CA长为半径的圆交AB于点D.若AC=6,求弧AD的长.
18.如图,已知以线段AB为直径作半圆O1,以线段AO1为直径作半圆O2,半径O1C交半圆O2于D点.试比较与的长.
19.如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠CAE=∠B=60°.
(1)求∠ADC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
20.如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°.
(1)求证:直线AD是⊙O的切线;
(2)若直径BC=4,求图中阴影部分的面积.
参考答案
1.答案为:C;
2.答案为:B.
3.答案为:D
4.答案为:C
5.答案为:C
6.答案为:C.
7.答案为:B.
8.答案为:B
9.答案为:D
10.答案为:A
11.答案为:110.
12.答案为:90°.
13.答案为:3π
14.答案为:2 -
15.答案为:cm2
16.答案为:﹣.
17.解:连接CD.
∵AC=CD,∴∠CAD=∠CDA.
∵∠ACB=90°,∠B=15°,∴∠CAD=75°,
∴∠ACD=30°.
∵AC=6,∴的长度为=π.
18.解:的长等于的长.
19.解:
(1)∵∠ABC与∠ADC都是弧AC所对的圆周角,
∴∠ADC=∠B=60°.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=30°.
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即?BA⊥AE.
∴AE是⊙O的切线.
(3)略.
20.解:(1)证明:连接OA,则∠COA=2∠B,
∵AD=AB,
∴∠B=∠D=30°,
∴∠COA=60°,
∴∠OAD=180°﹣60°﹣30°=90°,
∴OA⊥AD,
即CD是⊙O的切线;
(2)解:∵BC=4,∴OA=OC=2,
在Rt△OAD中,OA=2,∠D=30°,
∴OD=2OA=4,AD=2,所以S△OAD=OA?AD=×2×2=2,
因为∠COA=60°,所以S扇形COA==π,
所以S阴影=S△OAD﹣S扇形COA=2﹣.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
