一元二次方程的几种解法.
文档属性
| 名称 | 一元二次方程的几种解法. |

|
|
| 格式 | zip | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-01 00:00:00 | ||
图片预览




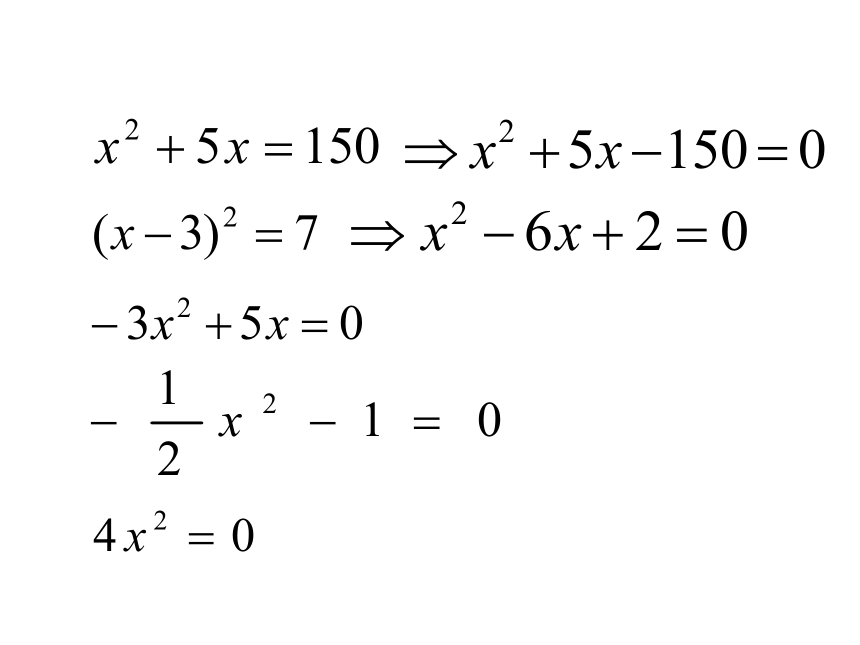






文档简介
(共58张PPT)
一元二次方程的几种解法
引例
剪一块面积为150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应怎样剪?
解:设这块铁片的宽为x cm,那么它的长为(x+5) cm. 根据题意,得
x(x+5)=150.
去括号,得 x2+5x=150.
一、一元二次方程的定义
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程.
1、只含一个未知数的
一元方程;
2、未知数的最高次数是2的
二次方程;
3、整式方程.
(不是整式方程)
(不是整式方程)
(不是一元方程)
(不是整式方程)
(不是整式方程)
(不是一元方程)
(不是二次方程)
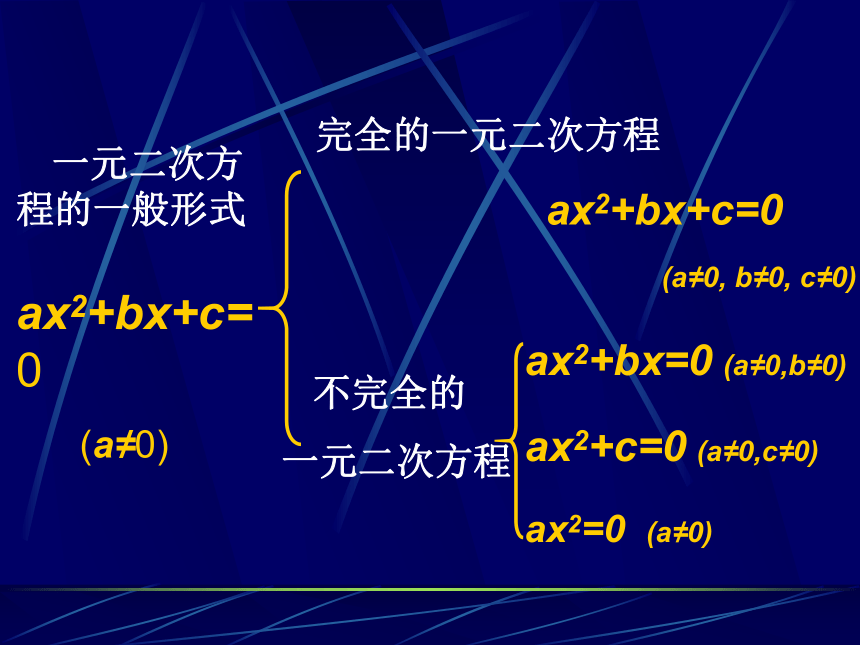
一元二次方程的一般形式
ax2+bx+c=0
(a≠0)
完全的一元二次方程
ax2+bx+c=0
(a≠0, b≠0, c≠0)
不完全的
一元二次方程
ax2+c=0 (a≠0,c≠0)
ax2+bx=0 (a≠0,b≠0)
ax2=0 (a≠0)
(1)化为一般形式后,
(2)二次项的系数是否为0
是判断一元二次方程的关键.
例1、方程 是否为一元二次方程?如果不是,说明理由;如果是,指出它的二次项、一次项系数及常数项.
解:去括号,得 3x2-3x=2x+4+8.
移项,得 3x2-3x-2x-4-8=0.
合并同类项,得 3x2-5x-12=0.
∴原方程是一元二次方程;二次项系数是3,一次项系数是 - 5,常数项是 – 12.
(1)
(2)
(3)
(4)
答:a=1, b=3, c= -2.
答:a=3, b=-5, c= 2.
答:a=-2, b=-5, c= 3.
答:a=6, b=1, c= -5.
练习:说出下列方程的二次项系数、一次项系数和常数项:
例2、 已知:关于x的方程
(2m-1)x2-(m-1)x=5m
是一元二次方程, 求:m的取值范围.
解:∵ 原方程是一元二次方程, ∴ 2m-1≠0,
∴ m≠ .
二、一元二次方程的解法
形如 的一元二次方程的解法:
ax2=0 (a≠0)
ax2=0 (a≠0)
2x2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
ax2=0 (a≠0)
5x2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
ax2=0 (a≠0)
-3x2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
ax2=0 (a≠0)
ax2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
4x2=36,
解:x2=9,
∴ x=±3.
即x1=3, x2= -3.
4x2=36,
x2=9,
4x2-36=0.
解:
∴ x=±3.
即x1=3, x2= -3.
当ac<0时 ,
形如 (a≠0,c ≠ 0)的一元二次方程的解法:
当ac>0时 ,此方程无实数解.
解法1、直接开平方法
如 x2=8, 2x2=9, -3x2+7=0,……等等.
x2=8.
2x2=9.
解:
-3x2+7=0.
解:
将(x-2)看作一个整体, 开平方,得:
解:系数化1,得
解:系数化1,得
开平方,得
解这两个一元一次方程,得
或
解法1:直接开平方法
凡形如 ax2+c=0 (a≠0, ac<0)
或 a(x+p)2+q=0 (a≠0, aq<0)
的一元二次方程都可用直接开平方法解.
写成()2 的形式,得
写成()2 的形式,得
写成()2 的形式,得
配方:左右两边同时加上一个常数,凑成完全平方,得
写成()2 的形式,得
配方:左右两边同时加上一个常数,凑成完全平方,得
写成()2 的形式,得
解:
移项:将常数项移到等号一边,得
配方:左右两边同时加上一个常数,凑成完全平方,得
写成()2 的形式,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
配方:左右两边同时加上一个常数,凑成完全平方,得
怎样配方:常数项是一次项系数一半的平方.
a2±2ab+b2=(a±b)2.
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
解法2:配方法
1、将二次项系数化为1:两边同时除以二次项系数;
2、移项:将常数项移到等号一边;
3、配方:左右两边同时加上一次项系数一半的平方;
4、等号左边写成( )2 的形式;
5、开平方:化成一元一次方程;
6、解一元一次方程;
配方法的基本步骤:
7、写出方程的解.
三、练习
练习 1、填空:
(1)
(2)
(3)
(4)
(5)
16
4
练习 1、填空:
(1)
(2)
(3)
(4)
(5)
2、用配方法解下列方程:
(1)
(2)
(3)
(4)
(1)
解:
(2)
解:
(3)
解:
(4)
解:
四、小结
1、一元二次方程的概念;
2、两种解法:(1)直接开平方法;
(2)配方法.
3、转化的数学思想.
五、作业
P15 A组 用直接开平方法解下列方程:
3、用配方法解下列方程:
B组 1、解下列关于x的方程:
补充:已知 (m-1)x2+mx=x-1 是 (1)一元二次方程时(2)一元二次方程时,求:m的取值范围.
一元二次方程的几种解法
引例
剪一块面积为150cm2的长方形铁片,使它的长比宽多5cm,这块铁片应怎样剪?
解:设这块铁片的宽为x cm,那么它的长为(x+5) cm. 根据题意,得
x(x+5)=150.
去括号,得 x2+5x=150.
一、一元二次方程的定义
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程.
1、只含一个未知数的
一元方程;
2、未知数的最高次数是2的
二次方程;
3、整式方程.
(不是整式方程)
(不是整式方程)
(不是一元方程)
(不是整式方程)
(不是整式方程)
(不是一元方程)
(不是二次方程)
一元二次方程的一般形式
ax2+bx+c=0
(a≠0)
完全的一元二次方程
ax2+bx+c=0
(a≠0, b≠0, c≠0)
不完全的
一元二次方程
ax2+c=0 (a≠0,c≠0)
ax2+bx=0 (a≠0,b≠0)
ax2=0 (a≠0)
(1)化为一般形式后,
(2)二次项的系数是否为0
是判断一元二次方程的关键.
例1、方程 是否为一元二次方程?如果不是,说明理由;如果是,指出它的二次项、一次项系数及常数项.
解:去括号,得 3x2-3x=2x+4+8.
移项,得 3x2-3x-2x-4-8=0.
合并同类项,得 3x2-5x-12=0.
∴原方程是一元二次方程;二次项系数是3,一次项系数是 - 5,常数项是 – 12.
(1)
(2)
(3)
(4)
答:a=1, b=3, c= -2.
答:a=3, b=-5, c= 2.
答:a=-2, b=-5, c= 3.
答:a=6, b=1, c= -5.
练习:说出下列方程的二次项系数、一次项系数和常数项:
例2、 已知:关于x的方程
(2m-1)x2-(m-1)x=5m
是一元二次方程, 求:m的取值范围.
解:∵ 原方程是一元二次方程, ∴ 2m-1≠0,
∴ m≠ .
二、一元二次方程的解法
形如 的一元二次方程的解法:
ax2=0 (a≠0)
ax2=0 (a≠0)
2x2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
ax2=0 (a≠0)
5x2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
ax2=0 (a≠0)
-3x2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
ax2=0 (a≠0)
ax2=0,
解:x2=0,
∴ x=0.
形如 的一元二次方程的解法:
4x2=36,
解:x2=9,
∴ x=±3.
即x1=3, x2= -3.
4x2=36,
x2=9,
4x2-36=0.
解:
∴ x=±3.
即x1=3, x2= -3.
当ac<0时 ,
形如 (a≠0,c ≠ 0)的一元二次方程的解法:
当ac>0时 ,此方程无实数解.
解法1、直接开平方法
如 x2=8, 2x2=9, -3x2+7=0,……等等.
x2=8.
2x2=9.
解:
-3x2+7=0.
解:
将(x-2)看作一个整体, 开平方,得:
解:系数化1,得
解:系数化1,得
开平方,得
解这两个一元一次方程,得
或
解法1:直接开平方法
凡形如 ax2+c=0 (a≠0, ac<0)
或 a(x+p)2+q=0 (a≠0, aq<0)
的一元二次方程都可用直接开平方法解.
写成()2 的形式,得
写成()2 的形式,得
写成()2 的形式,得
配方:左右两边同时加上一个常数,凑成完全平方,得
写成()2 的形式,得
配方:左右两边同时加上一个常数,凑成完全平方,得
写成()2 的形式,得
解:
移项:将常数项移到等号一边,得
配方:左右两边同时加上一个常数,凑成完全平方,得
写成()2 的形式,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
配方:左右两边同时加上一个常数,凑成完全平方,得
怎样配方:常数项是一次项系数一半的平方.
a2±2ab+b2=(a±b)2.
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
写成()2 的形式,得
配方:左右两边同时加上一次项系数一半的平方,得
解:
移项:将常数项移到等号一边,得
开平方,得
解这两个方程,得
二次项系数化1:两边同时除以二次项系数,得
解法2:配方法
1、将二次项系数化为1:两边同时除以二次项系数;
2、移项:将常数项移到等号一边;
3、配方:左右两边同时加上一次项系数一半的平方;
4、等号左边写成( )2 的形式;
5、开平方:化成一元一次方程;
6、解一元一次方程;
配方法的基本步骤:
7、写出方程的解.
三、练习
练习 1、填空:
(1)
(2)
(3)
(4)
(5)
16
4
练习 1、填空:
(1)
(2)
(3)
(4)
(5)
2、用配方法解下列方程:
(1)
(2)
(3)
(4)
(1)
解:
(2)
解:
(3)
解:
(4)
解:
四、小结
1、一元二次方程的概念;
2、两种解法:(1)直接开平方法;
(2)配方法.
3、转化的数学思想.
五、作业
P15 A组 用直接开平方法解下列方程:
3、用配方法解下列方程:
B组 1、解下列关于x的方程:
补充:已知 (m-1)x2+mx=x-1 是 (1)一元二次方程时(2)一元二次方程时,求:m的取值范围.
同课章节目录
