23.2.3 关于原点对称的点的坐标同步练习 2021-2022学年人教版数学九年级上册(word版含答案)
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标同步练习 2021-2022学年人教版数学九年级上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览


文档简介
23.2.3 关于原点对称的点的坐标
命题点 1 关于原点对称的点的坐标
1.若点A(-3,2)关于原点的对称点是点B,点B关于x轴的对称点是点C,则点C的坐标是 ( )
A.(3,2) B.(-3,2)
C.(3,-2) D.(-2,3)
2.点P(-3,-1)关于x轴对称的点P1的坐标是 ,关于y轴对称的点P2的坐标是 ,关于原点对称的点P3的坐标为 .?
3.在平面直角坐标系中,若点A(a,-5)和点A'(8,-b)关于原点对称,则a2-b2= .?
4.已知?ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为 .?
命题点 2 关于原点对称的点所在象限问题
5.已知点P(-1,m2+1)与点Q关于原点对称,则点Q一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.若点P(-a,a-3)关于原点对称的点是第二象限内的点,则a满足 ( )
A.a>3 B.0 C.a<0 D.a<0或a>3
命题点 3 图形变换与坐标变化的综合
7.把△ABC各点的横坐标都乘-1,纵坐标都乘-1,符合上述要求的图是 ( )
8.在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为 ( )
A.(4,-3) B.(-4,3) C.(-3,4) D.(-3,-4)
9.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
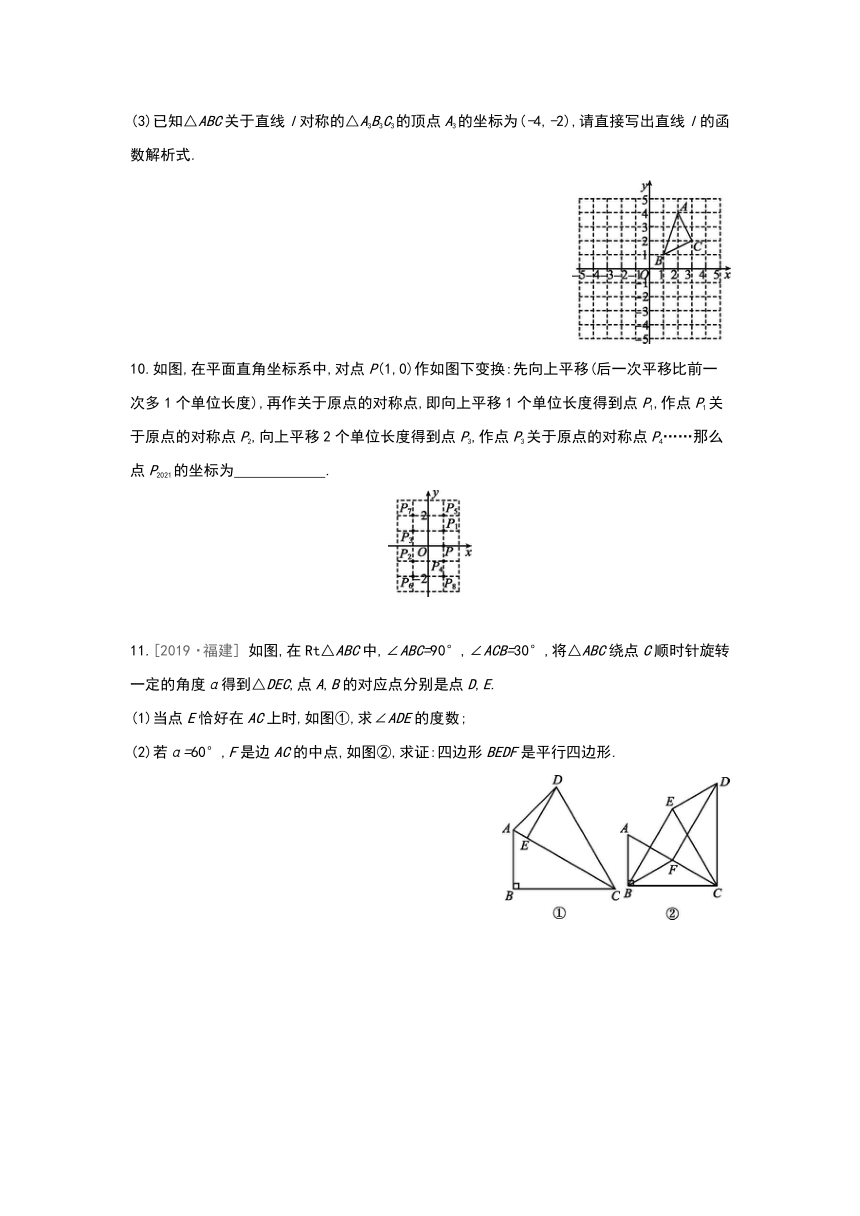
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
10.如图,在平面直角坐标系中,对点P(1,0)作如图下变换:先向上平移(后一次平移比前一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4……那么点P2021的坐标为 .?
11.[2019·福建] 如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A,B的对应点分别是点D,E.
(1)当点E恰好在AC上时,如图①,求∠ADE的度数;
(2)若α=60°,F是边AC的中点,如图②,求证:四边形BEDF是平行四边形.
12.[2018·青海] 请认真阅读下面的数学小探究系列,完成所提出的问题:
(1)探究1:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.求证:△BCD的面积为12a2.(提示:过点D作BC边上的高DE,可证△ABC≌△BDE)
(2)探究2:如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由.
(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.
13.[2020·重庆A卷] 如图,在Rt△ABC中,∠BAC=90°,AB=AC,D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.F是DE的中点,连接CF.
(1)求证:CF=22AD;
(2)如图②所示,在点D运动的过程中,当BD=2CD时,分别延长CF,BA,相交于点G,猜想AG与BC存在的数量关系,并证明你猜想的结论;
(3)在点D运动的过程中,在线段AD上存在一点P,使PA+PB+PC的值最小.当PA+PB+PC的值最小时,PA的长为m,请直接用含m的式子表示CE的长.
答案
1.A 2.(-3,1) (3,-1) (3,1) 3.39
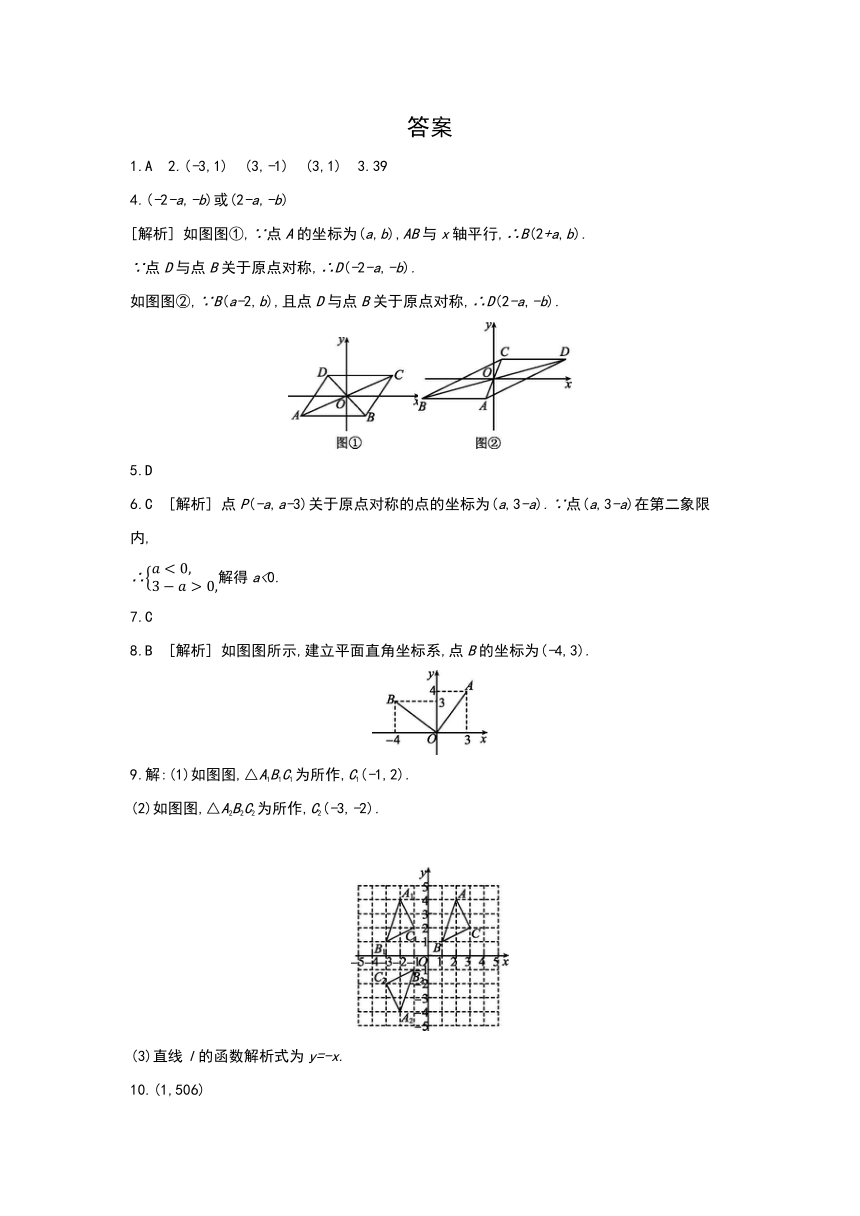
4.(-2-a,-b)或(2-a,-b)
[解析] 如图图①,∵点A的坐标为(a,b),AB与x轴平行,∴B(2+a,b).
∵点D与点B关于原点对称,∴D(-2-a,-b).
如图图②,∵B(a-2,b),且点D与点B关于原点对称,∴D(2-a,-b).
5.D
6.C [解析] 点P(-a,a-3)关于原点对称的点的坐标为(a,3-a).∵点(a,3-a)在第二象限内,
∴a<0,3?a>0,解得a<0.
7.C
8.B [解析] 如图图所示,建立平面直角坐标系,点B的坐标为(-4,3).
9.解:(1)如图图,△A1B1C1为所作,C1(-1,2).
(2)如图图,△A2B2C2为所作,C2(-3,-2).
(3)直线l的函数解析式为y=-x.
10.(1,506)
[解析] 根据题意可列出下面的表格:
向上平移
关于原点的对称点
向上平移
关于原点的对称点
P1(1,1)
P2(-1,-1)
P3(-1,1)
P4(1,-1)
P5(1,2)
P6(-1,-2)
P7(-1,2)
P8(1,-2)
P9(1,3)
P10(-1,-3)
P11(-1,3)
P12(1,-3)
…
…
…
…
观察表格可知:这些点平均分布在四个象限中,序号除以4余1的点在第一象限,横坐标都是1,纵坐标为序号减1除以4的商加1;序号除以4余2的点是序号除以4余1的点关于原点的对称点;序号能被4整除的点在第四象限,横坐标为1,纵坐标为序号除以4的商的相反数;序号除以4余3的点在第二象限,是序号能被4整除的点关于原点的对称点.因为2021÷4=505……1,所以点P2021在第一象限,坐标为(1,506).
11.解:(1)∵△ABC绕点C顺时针旋转角α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°.
∵CA=CD,
∴∠CAD=∠CDA=12(180°-30°)=75°,
∴∠ADE=90°-75°=15°.
(2)证明:连接AD.
∵F是边AC的中点,∠ABC=90°,
∴BF=CF=12AC.
∵∠ACB=30°,∴AB=12AC,∴BF=AB=CF.
∵△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,BC=CE,CD=CA,DE=AB,
∴DE=BF,△ACD和△BCE均为等边三角形,
∴BE=CB.
∵F为△ACD的边AC的中点,∴DF⊥AC,
∴∠CFD=∠ABC=90°,∴Rt△CFD≌Rt△ABC,
∴DF=BC,∴DF=BE.
又∵BF=DE,∴四边形BEDF是平行四边形.
12.解:(1)证明:如图①,过点D作DE⊥CB交CB的延长线于点E,
∴∠BED=∠ACB=90°.
由旋转知,AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°,∴∠A=∠DBE.
在△ABC和△BDE中,∠ACB=∠BED,∠A=∠DBE,AB=BD,
∴△ABC≌△BDE(AAS),∴BC=DE=a.
∵S△BCD=12BC·DE,∴S△BCD=12a2.
(2)△BCD的面积为12a2.
理由:如图②,过点D作CB的垂线,与CB的延长线交于点E,
∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴AB=BD,∠ABD=90°,∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°,∴∠A=∠DBE.
在△ABC和△BDE中,∠ACB=∠BED,∠A=∠DBE,AB=BD,
∴△ABC≌△BDE(AAS),∴BC=DE=a.
∵S△BCD=12BC·DE,∴S△BCD=12a2.
(3)如图③,过点A作AF⊥BC于点F,过点D作DE⊥CB交CB的延长线于点E,
∴∠AFB=∠E=90°,BF=12BC=12a,
∴∠FAB+∠ABF=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴∠ABD=90°,AB=BD,
∴∠ABF+∠EBD=90°,∴∠FAB=∠EBD.
在△AFB和△BED中,∠AFB=∠BED=90°,∠FAB=∠EBD,AB=BD,
∴△AFB≌△BED(AAS),∴BF=DE=12a,
∴S△BCD=12BC·DE=12·a·12a=14a2.
13.[解析] (1)通过证明△ABD≌△ACE得到∠ABD=∠ACE,进而得到∠ECD=∠ACB+∠ACE=90°.
因为CF是Rt△EDC的中线,
所以CF=12DE=22AD;
(2)连接AF,DG,DG与AC交于点M,由AF=CF=DF=GF可证得∠GDC=90°,从而得到△CDM和△BDG都为等腰直角三角形,BD=DG=2CD=2MG,故BC=3MG=32AG,问题得解;
(3)当AD⊥BC时,在AD上存在点P,满足条件.此时,CE的长为3+32m.
解:(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE,∴∠ABD=∠ACE.
∵AB=AC,∠BAC=90°,∴∠ABD=∠ACB=45°,
∴∠ACE=∠ABD=45°,
∴∠ECD=∠ACB+∠ACE=90°.
∵F是DE的中点,∴CF=12DE.
∵AD=AE,∠DAE=90°,
∴DE=2AD,∴CF=22AD.
(2)猜想:BCAG=32.
证明:如图,连接AF,DG,DG与AC交于点M.
由(1)易知,AF=CF=DF=12DE,∴∠FAC=∠FCA.
∵∠GAC=90°,
∴∠FAG+∠FAC=90°,∠FGA+∠FCA=90°,
∴∠FAG=∠FGA,∴AF=GF,∴GF=DF=CF,
∴∠FGD=∠FDG,∠FDC=∠FCD.
∵∠FGD+∠FDG+∠FDC+∠FCD=180°,
∴∠FDG+∠FDC=90°,∴∠GDC=90°.
∵∠B=45°,∴∠AGD=∠ACD=45°,
∴BD=GD,CD=MD,∠AMG=∠DMC=45°.
∵∠GAC=90°,∴MG=2AG.
∵BD=2CD,∴BD=DG=2CD=2DM=DM+MG,
∴DM=MG,∴BC=BD+CD=3MG=32AG,
即BCAG=32.
(3)CE=3+32m.
命题点 1 关于原点对称的点的坐标
1.若点A(-3,2)关于原点的对称点是点B,点B关于x轴的对称点是点C,则点C的坐标是 ( )
A.(3,2) B.(-3,2)
C.(3,-2) D.(-2,3)
2.点P(-3,-1)关于x轴对称的点P1的坐标是 ,关于y轴对称的点P2的坐标是 ,关于原点对称的点P3的坐标为 .?
3.在平面直角坐标系中,若点A(a,-5)和点A'(8,-b)关于原点对称,则a2-b2= .?
4.已知?ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2.若点A的坐标为(a,b),则点D的坐标为 .?
命题点 2 关于原点对称的点所在象限问题
5.已知点P(-1,m2+1)与点Q关于原点对称,则点Q一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.若点P(-a,a-3)关于原点对称的点是第二象限内的点,则a满足 ( )
A.a>3 B.0
命题点 3 图形变换与坐标变化的综合
7.把△ABC各点的横坐标都乘-1,纵坐标都乘-1,符合上述要求的图是 ( )
8.在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为 ( )
A.(4,-3) B.(-4,3) C.(-3,4) D.(-3,-4)
9.在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
10.如图,在平面直角坐标系中,对点P(1,0)作如图下变换:先向上平移(后一次平移比前一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位长度得到点P1,作点P1关于原点的对称点P2,向上平移2个单位长度得到点P3,作点P3关于原点的对称点P4……那么点P2021的坐标为 .?
11.[2019·福建] 如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A,B的对应点分别是点D,E.
(1)当点E恰好在AC上时,如图①,求∠ADE的度数;
(2)若α=60°,F是边AC的中点,如图②,求证:四边形BEDF是平行四边形.
12.[2018·青海] 请认真阅读下面的数学小探究系列,完成所提出的问题:
(1)探究1:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.求证:△BCD的面积为12a2.(提示:过点D作BC边上的高DE,可证△ABC≌△BDE)
(2)探究2:如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由.
(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.
13.[2020·重庆A卷] 如图,在Rt△ABC中,∠BAC=90°,AB=AC,D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.F是DE的中点,连接CF.
(1)求证:CF=22AD;
(2)如图②所示,在点D运动的过程中,当BD=2CD时,分别延长CF,BA,相交于点G,猜想AG与BC存在的数量关系,并证明你猜想的结论;
(3)在点D运动的过程中,在线段AD上存在一点P,使PA+PB+PC的值最小.当PA+PB+PC的值最小时,PA的长为m,请直接用含m的式子表示CE的长.
答案
1.A 2.(-3,1) (3,-1) (3,1) 3.39
4.(-2-a,-b)或(2-a,-b)
[解析] 如图图①,∵点A的坐标为(a,b),AB与x轴平行,∴B(2+a,b).
∵点D与点B关于原点对称,∴D(-2-a,-b).
如图图②,∵B(a-2,b),且点D与点B关于原点对称,∴D(2-a,-b).
5.D
6.C [解析] 点P(-a,a-3)关于原点对称的点的坐标为(a,3-a).∵点(a,3-a)在第二象限内,
∴a<0,3?a>0,解得a<0.
7.C
8.B [解析] 如图图所示,建立平面直角坐标系,点B的坐标为(-4,3).
9.解:(1)如图图,△A1B1C1为所作,C1(-1,2).
(2)如图图,△A2B2C2为所作,C2(-3,-2).
(3)直线l的函数解析式为y=-x.
10.(1,506)
[解析] 根据题意可列出下面的表格:
向上平移
关于原点的对称点
向上平移
关于原点的对称点
P1(1,1)
P2(-1,-1)
P3(-1,1)
P4(1,-1)
P5(1,2)
P6(-1,-2)
P7(-1,2)
P8(1,-2)
P9(1,3)
P10(-1,-3)
P11(-1,3)
P12(1,-3)
…
…
…
…
观察表格可知:这些点平均分布在四个象限中,序号除以4余1的点在第一象限,横坐标都是1,纵坐标为序号减1除以4的商加1;序号除以4余2的点是序号除以4余1的点关于原点的对称点;序号能被4整除的点在第四象限,横坐标为1,纵坐标为序号除以4的商的相反数;序号除以4余3的点在第二象限,是序号能被4整除的点关于原点的对称点.因为2021÷4=505……1,所以点P2021在第一象限,坐标为(1,506).
11.解:(1)∵△ABC绕点C顺时针旋转角α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°.
∵CA=CD,
∴∠CAD=∠CDA=12(180°-30°)=75°,
∴∠ADE=90°-75°=15°.
(2)证明:连接AD.
∵F是边AC的中点,∠ABC=90°,
∴BF=CF=12AC.
∵∠ACB=30°,∴AB=12AC,∴BF=AB=CF.
∵△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,BC=CE,CD=CA,DE=AB,
∴DE=BF,△ACD和△BCE均为等边三角形,
∴BE=CB.
∵F为△ACD的边AC的中点,∴DF⊥AC,
∴∠CFD=∠ABC=90°,∴Rt△CFD≌Rt△ABC,
∴DF=BC,∴DF=BE.
又∵BF=DE,∴四边形BEDF是平行四边形.
12.解:(1)证明:如图①,过点D作DE⊥CB交CB的延长线于点E,
∴∠BED=∠ACB=90°.
由旋转知,AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°,∴∠A=∠DBE.
在△ABC和△BDE中,∠ACB=∠BED,∠A=∠DBE,AB=BD,
∴△ABC≌△BDE(AAS),∴BC=DE=a.
∵S△BCD=12BC·DE,∴S△BCD=12a2.
(2)△BCD的面积为12a2.
理由:如图②,过点D作CB的垂线,与CB的延长线交于点E,
∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴AB=BD,∠ABD=90°,∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°,∴∠A=∠DBE.
在△ABC和△BDE中,∠ACB=∠BED,∠A=∠DBE,AB=BD,
∴△ABC≌△BDE(AAS),∴BC=DE=a.
∵S△BCD=12BC·DE,∴S△BCD=12a2.
(3)如图③,过点A作AF⊥BC于点F,过点D作DE⊥CB交CB的延长线于点E,
∴∠AFB=∠E=90°,BF=12BC=12a,
∴∠FAB+∠ABF=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴∠ABD=90°,AB=BD,
∴∠ABF+∠EBD=90°,∴∠FAB=∠EBD.
在△AFB和△BED中,∠AFB=∠BED=90°,∠FAB=∠EBD,AB=BD,
∴△AFB≌△BED(AAS),∴BF=DE=12a,
∴S△BCD=12BC·DE=12·a·12a=14a2.
13.[解析] (1)通过证明△ABD≌△ACE得到∠ABD=∠ACE,进而得到∠ECD=∠ACB+∠ACE=90°.
因为CF是Rt△EDC的中线,
所以CF=12DE=22AD;
(2)连接AF,DG,DG与AC交于点M,由AF=CF=DF=GF可证得∠GDC=90°,从而得到△CDM和△BDG都为等腰直角三角形,BD=DG=2CD=2MG,故BC=3MG=32AG,问题得解;
(3)当AD⊥BC时,在AD上存在点P,满足条件.此时,CE的长为3+32m.
解:(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△ABD和△ACE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE,∴∠ABD=∠ACE.
∵AB=AC,∠BAC=90°,∴∠ABD=∠ACB=45°,
∴∠ACE=∠ABD=45°,
∴∠ECD=∠ACB+∠ACE=90°.
∵F是DE的中点,∴CF=12DE.
∵AD=AE,∠DAE=90°,
∴DE=2AD,∴CF=22AD.
(2)猜想:BCAG=32.
证明:如图,连接AF,DG,DG与AC交于点M.
由(1)易知,AF=CF=DF=12DE,∴∠FAC=∠FCA.
∵∠GAC=90°,
∴∠FAG+∠FAC=90°,∠FGA+∠FCA=90°,
∴∠FAG=∠FGA,∴AF=GF,∴GF=DF=CF,
∴∠FGD=∠FDG,∠FDC=∠FCD.
∵∠FGD+∠FDG+∠FDC+∠FCD=180°,
∴∠FDG+∠FDC=90°,∴∠GDC=90°.
∵∠B=45°,∴∠AGD=∠ACD=45°,
∴BD=GD,CD=MD,∠AMG=∠DMC=45°.
∵∠GAC=90°,∴MG=2AG.
∵BD=2CD,∴BD=DG=2CD=2DM=DM+MG,
∴DM=MG,∴BC=BD+CD=3MG=32AG,
即BCAG=32.
(3)CE=3+32m.
同课章节目录
