人教版 八年级数学上册 12.2 三角形全等的判定 同步课时训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册 12.2 三角形全等的判定 同步课时训练(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 460.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览



文档简介
人教版 八年级数学上册 12.2 三角形全等的判定 同步课时训练
一、选择题
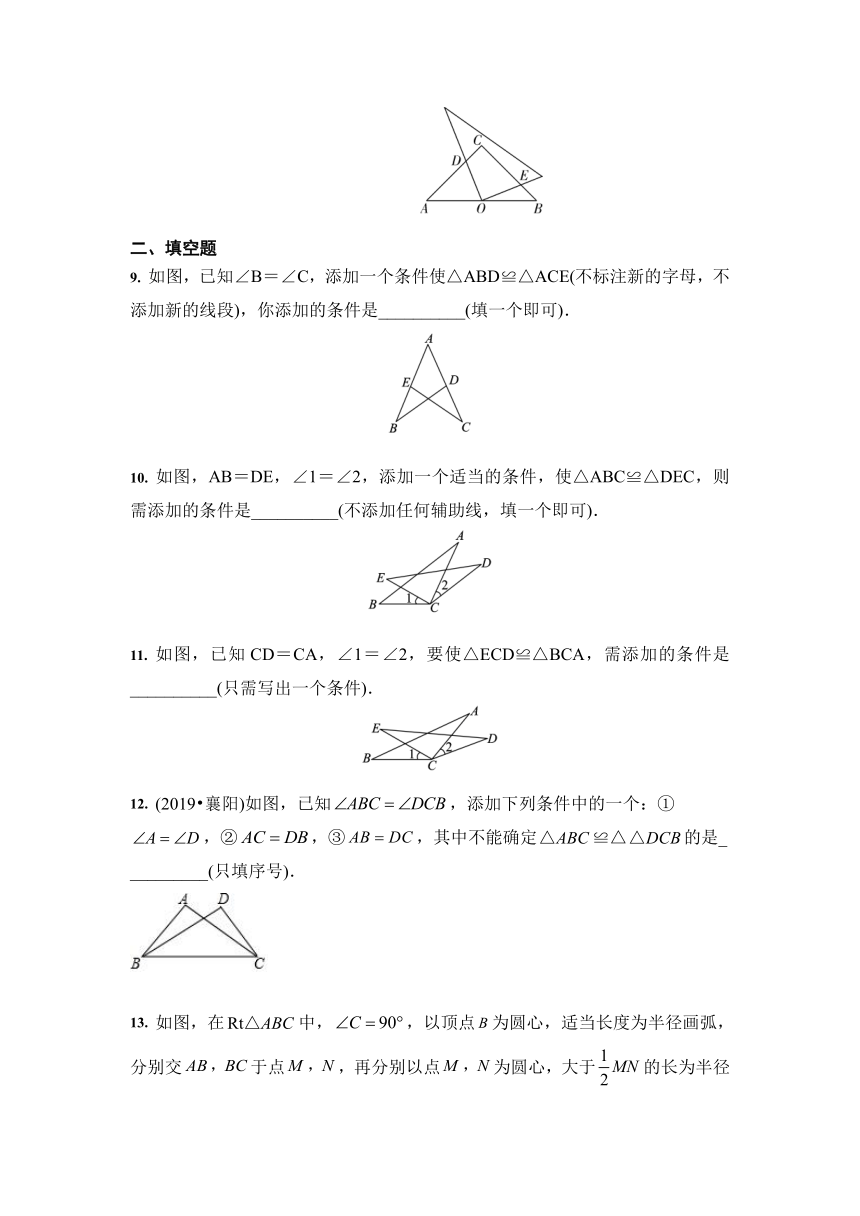
1. 如图,AD=AE,若利用“SAS”证明△ABE≌△ACD,则需要添加的条件是( )
A.AB=AC
B.∠B=∠C
C.∠AEB=∠ADC
D.∠A=∠B
2. 如图所示,P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
A.HL B.ASA C.AAS D.SAS
3. 如图所示,已知AB∥DE,点B,E,C,F在同一直线上,AB=DE,BE=CF,∠B=32°,∠A=78°,则∠F等于( )
A.55° B.65° C.60° D.70°
4. 如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是 ( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠A=∠DEF,BC=FD
5. 已知△ABC的六个元素,下列甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
6. 如图,若AB=AC,AD=AE,∠BAC=∠DAE,则∠ABD等于( )
A.∠EAC B.∠ADE C.∠BAD D.∠ACE
7. 现已知线段a,b(a小惠:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点A为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是 ( )
A.小惠的作法正确,小雷的作法错误
B.小雷的作法正确,小惠的作法错误
C.两人的作法都正确
D.两人的作法都错误
8. 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE等于( )
A. B. C. 2 D.
二、填空题
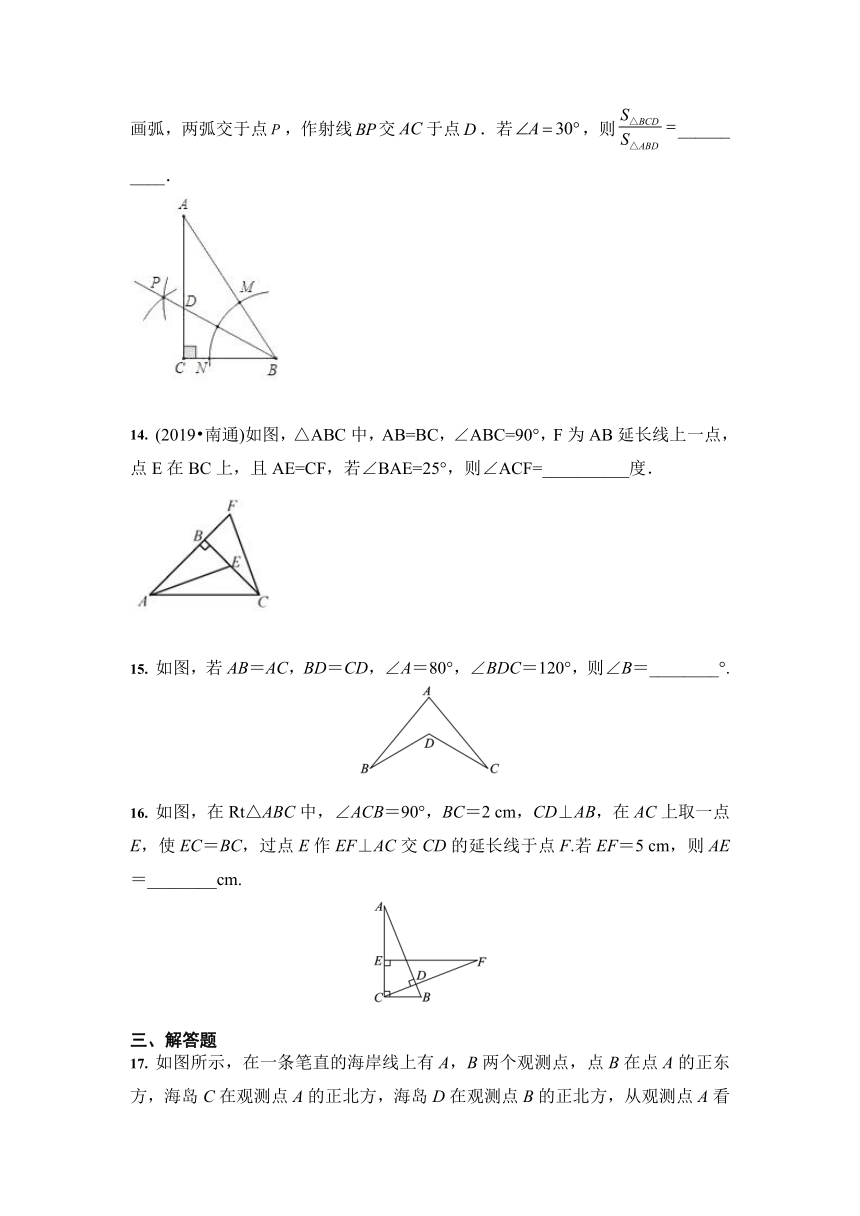
9. 如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字母,不添加新的线段),你添加的条件是__________(填一个即可).
10. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
11. 如图,已知CD=CA,∠1=∠2,要使△ECD≌△BCA,需添加的条件是__________(只需写出一个条件).
12. (2019?襄阳)如图,已知,添加下列条件中的一个:①,②,③,其中不能确定≌△的是__________(只填序号).
13. 如图,在中,,以顶点为圆心,适当长度为半径画弧,分别交于点,再分别以点为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,则__________.
14. (2019?南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.
15. 如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.
16. 如图,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5 cm,则AE=________cm.
三、解答题
17. 如图所示,在一条笔直的海岸线上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸线的距离相等吗?为什么?
18. 如图,已知AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,如果AD=AF,AC=AE,求证:BC=BE.
19. 已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE、CF,求证:△ADE≌△CDF.
20. 操作探究如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2 cm,BC=5 cm,如图K-10-17,量得第四根木条DC=5 cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2 cm,量得木条CD=5 cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30 cm的三角形,求出木条AD,BC的长度.
人教版 八年级数学上册 12.2 三角形全等的判定 同步课时训练-答案
一、选择题
1. 【答案】A
2. 【答案】A
3. 【答案】D [解析] 因为AB∥DE,所以∠B=∠DEF.由条件BE=CF知BC=EF.结合条件AB=DE,可由“SAS”判定△ABC≌△DEF,所以∠F=∠ACB=180°-(∠A+∠B)=180°-(78°+32°)=70°.
4. 【答案】C [解析] A.添加BC=FD,AC=ED,可利用“SAS”判定△ABC≌△EFD;
B.添加∠A=∠DEF,AC=ED,可利用“ASA”判定△ABC≌△EFD;
C.添加AC=ED,AB=EF,不能判定△ABC≌△EFD;
D.添加∠A=∠DEF,BC=FD,可利用“AAS”判定△ABC≌△EFD.
5. 【答案】D
6. 【答案】D [解析] ∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE.
7. 【答案】A [解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.
8. 【答案】B 【解析】如解图,连接OC,由已知条件易得∠A=∠OCE,CO=AO,∠DOE=∠COA,∴∠DOE-∠COD=∠COA-∠COD,即∠AOD=∠COE,∴△AOD≌△COE(ASA),∴AD=CE,进而得CD+CE=CD+AD=AC=AB=,故选B.
二、填空题
9. 【答案】答案不唯一,如AB=AC
10. 【答案】答案不唯一,如∠B=∠E
11. 【答案】答案不唯一,如CE=CB [解析] 由∠1=∠2,可得∠DCE=∠ACB,又∵CD=CA,∴添加CE=CB,可根据“SAS”判定两个三角形全等.
12. 【答案】②
【解析】∵已知,且,
∴若添加①,则可由AAS判定≌;
若添加②,则属于边边角的顺序,不能判定≌;
若添加③,则属于边角边的顺序,可以判定≌.
故答案为:②.
13. 【答案】
【解析】由作法得平分,
∵,,∴,
∴,∴,
在中,,∴,
∴.故答案为:.
14. 【答案】70
【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,
在Rt△ABE和Rt△CBF中,,∴Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.
15. 【答案】20 [解析] 如图,过点D作射线AF.
在△BAD和△CAD中,
∴△BAD≌△CAD(SSS).
∴∠BAD=∠CAD,∠B=∠C.
∵∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD,
即∠BDC=∠B+∠C+∠BAC.
∵∠BAC=80°,∠BDC=120°,
∴∠B=∠C=20°.
16. 【答案】3 [解析] ∵∠ACB=90°,∴∠ECF+∠BCD=90°.∵CD⊥AB,∴∠BCD+∠B=90°.
∴∠ECF=∠B.
在△ABC和△FCE中,
∴△ABC≌△FCE(ASA).∴AC=FE.
∵AE=AC-CE,BC=2 cm,EF=5 cm,
∴AE=5-2=3(cm).
三、解答题
17. 【答案】
解:相等.理由:设AD,BC相交于点O.
∵∠CAD=∠CBD,∠COA=∠DOB,
∴由三角形内角和定理,得∠C=∠D.
由已知得∠CAB=∠DBA=90°.
在△CAB和△DBA中,
∴△CAB≌△DBA.
∴CA=DB.
∴海岛C,D到观测点A,B所在海岸线的距离相等.
18. 【答案】
证明:∵AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,∴∠D=∠F=90°.
在Rt△ADC和Rt△AFE中,
∴Rt△ADC≌Rt△AFE(HL).∴CD=EF.
在Rt△ABD和Rt△ABF中,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.∴BD-CD=BF-EF,
即BC=BE.
19. 【答案】
证明:∵四边形ABCD是菱形,
∴AD=CD.(2分)
又∵E、F分别为边CD、AD的中点,
∴DE=DF.(4分)
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS).(8分)
20. 【答案】
解:(1)相等.
理由:如图,连接AC.
在△ACD和△ACB中,
∴△ACD≌△ACB(SSS).
∴∠B=∠D.
(2)设AD=x cm,BC=y cm.
当点C,D均在BA的延长线上且点C在点D右侧时,由题意,得
解得
此时AD=13 cm,BC=10 cm.
经检验,符合题意.
当点C,D均在BA的延长线上且点C在点D左侧时,由题意,得
解得
此时AD=8 cm,BC=15 cm.
∵5+8<2+15,∴不合题意.
综上,AD=13 cm,BC=10 cm.
一、选择题
1. 如图,AD=AE,若利用“SAS”证明△ABE≌△ACD,则需要添加的条件是( )
A.AB=AC
B.∠B=∠C
C.∠AEB=∠ADC
D.∠A=∠B
2. 如图所示,P是∠BAC内一点,PE⊥AB于点E,PF⊥AC于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
A.HL B.ASA C.AAS D.SAS
3. 如图所示,已知AB∥DE,点B,E,C,F在同一直线上,AB=DE,BE=CF,∠B=32°,∠A=78°,则∠F等于( )
A.55° B.65° C.60° D.70°
4. 如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是 ( )
A.BC=FD,AC=ED B.∠A=∠DEF,AC=ED
C.AC=ED,AB=EF D.∠A=∠DEF,BC=FD
5. 已知△ABC的六个元素,下列甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙 B.只有丙 C.甲和乙 D.乙和丙
6. 如图,若AB=AC,AD=AE,∠BAC=∠DAE,则∠ABD等于( )
A.∠EAC B.∠ADE C.∠BAD D.∠ACE
7. 现已知线段a,b(a
小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.
则下列说法中正确的是 ( )
A.小惠的作法正确,小雷的作法错误
B.小雷的作法正确,小惠的作法错误
C.两人的作法都正确
D.两人的作法都错误
8. 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE等于( )
A. B. C. 2 D.
二、填空题
9. 如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字母,不添加新的线段),你添加的条件是__________(填一个即可).
10. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
11. 如图,已知CD=CA,∠1=∠2,要使△ECD≌△BCA,需添加的条件是__________(只需写出一个条件).
12. (2019?襄阳)如图,已知,添加下列条件中的一个:①,②,③,其中不能确定≌△的是__________(只填序号).
13. 如图,在中,,以顶点为圆心,适当长度为半径画弧,分别交于点,再分别以点为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,则__________.
14. (2019?南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.
15. 如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.
16. 如图,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5 cm,则AE=________cm.
三、解答题
17. 如图所示,在一条笔直的海岸线上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸线的距离相等吗?为什么?
18. 如图,已知AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,如果AD=AF,AC=AE,求证:BC=BE.
19. 已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE、CF,求证:△ADE≌△CDF.
20. 操作探究如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2 cm,BC=5 cm,如图K-10-17,量得第四根木条DC=5 cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2 cm,量得木条CD=5 cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A,C,D能构成周长为30 cm的三角形,求出木条AD,BC的长度.
人教版 八年级数学上册 12.2 三角形全等的判定 同步课时训练-答案
一、选择题
1. 【答案】A
2. 【答案】A
3. 【答案】D [解析] 因为AB∥DE,所以∠B=∠DEF.由条件BE=CF知BC=EF.结合条件AB=DE,可由“SAS”判定△ABC≌△DEF,所以∠F=∠ACB=180°-(∠A+∠B)=180°-(78°+32°)=70°.
4. 【答案】C [解析] A.添加BC=FD,AC=ED,可利用“SAS”判定△ABC≌△EFD;
B.添加∠A=∠DEF,AC=ED,可利用“ASA”判定△ABC≌△EFD;
C.添加AC=ED,AB=EF,不能判定△ABC≌△EFD;
D.添加∠A=∠DEF,BC=FD,可利用“AAS”判定△ABC≌△EFD.
5. 【答案】D
6. 【答案】D [解析] ∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE.
7. 【答案】A [解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.
8. 【答案】B 【解析】如解图,连接OC,由已知条件易得∠A=∠OCE,CO=AO,∠DOE=∠COA,∴∠DOE-∠COD=∠COA-∠COD,即∠AOD=∠COE,∴△AOD≌△COE(ASA),∴AD=CE,进而得CD+CE=CD+AD=AC=AB=,故选B.
二、填空题
9. 【答案】答案不唯一,如AB=AC
10. 【答案】答案不唯一,如∠B=∠E
11. 【答案】答案不唯一,如CE=CB [解析] 由∠1=∠2,可得∠DCE=∠ACB,又∵CD=CA,∴添加CE=CB,可根据“SAS”判定两个三角形全等.
12. 【答案】②
【解析】∵已知,且,
∴若添加①,则可由AAS判定≌;
若添加②,则属于边边角的顺序,不能判定≌;
若添加③,则属于边角边的顺序,可以判定≌.
故答案为:②.
13. 【答案】
【解析】由作法得平分,
∵,,∴,
∴,∴,
在中,,∴,
∴.故答案为:.
14. 【答案】70
【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,
在Rt△ABE和Rt△CBF中,,∴Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.
15. 【答案】20 [解析] 如图,过点D作射线AF.
在△BAD和△CAD中,
∴△BAD≌△CAD(SSS).
∴∠BAD=∠CAD,∠B=∠C.
∵∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD,
即∠BDC=∠B+∠C+∠BAC.
∵∠BAC=80°,∠BDC=120°,
∴∠B=∠C=20°.
16. 【答案】3 [解析] ∵∠ACB=90°,∴∠ECF+∠BCD=90°.∵CD⊥AB,∴∠BCD+∠B=90°.
∴∠ECF=∠B.
在△ABC和△FCE中,
∴△ABC≌△FCE(ASA).∴AC=FE.
∵AE=AC-CE,BC=2 cm,EF=5 cm,
∴AE=5-2=3(cm).
三、解答题
17. 【答案】
解:相等.理由:设AD,BC相交于点O.
∵∠CAD=∠CBD,∠COA=∠DOB,
∴由三角形内角和定理,得∠C=∠D.
由已知得∠CAB=∠DBA=90°.
在△CAB和△DBA中,
∴△CAB≌△DBA.
∴CA=DB.
∴海岛C,D到观测点A,B所在海岸线的距离相等.
18. 【答案】
证明:∵AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,∴∠D=∠F=90°.
在Rt△ADC和Rt△AFE中,
∴Rt△ADC≌Rt△AFE(HL).∴CD=EF.
在Rt△ABD和Rt△ABF中,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.∴BD-CD=BF-EF,
即BC=BE.
19. 【答案】
证明:∵四边形ABCD是菱形,
∴AD=CD.(2分)
又∵E、F分别为边CD、AD的中点,
∴DE=DF.(4分)
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS).(8分)
20. 【答案】
解:(1)相等.
理由:如图,连接AC.
在△ACD和△ACB中,
∴△ACD≌△ACB(SSS).
∴∠B=∠D.
(2)设AD=x cm,BC=y cm.
当点C,D均在BA的延长线上且点C在点D右侧时,由题意,得
解得
此时AD=13 cm,BC=10 cm.
经检验,符合题意.
当点C,D均在BA的延长线上且点C在点D左侧时,由题意,得
解得
此时AD=8 cm,BC=15 cm.
∵5+8<2+15,∴不合题意.
综上,AD=13 cm,BC=10 cm.
