22.1.3.1二次函数y=ax2+k的图象和性质 能力提升卷 2021-2022学年人教版九年级数学上册 (Word版 含答案)
文档属性
| 名称 | 22.1.3.1二次函数y=ax2+k的图象和性质 能力提升卷 2021-2022学年人教版九年级数学上册 (Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 128.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 11:58:05 | ||
图片预览

文档简介
人教版九年级数学上册
22.1.3.1二次函数y=ax2+k的图象和性质
能力提升卷
一、选择题(共8小题,4*8=32)
1.在抛物线y=-x2+1上的一个点是( )
A.(1,0) B.(0,0)
C.(0,-1) D.(1,1)
2.抛物线y=ax2+k的顶点是(0,2),且形状及开口方向与抛物线y=-x2相同,则a,k的值分别为( )
A.-,2 B.-,-2
C.,2 D.,-2
3.二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
4.将抛物线y=2x2+3平移后得到抛物线y=2x2,平移的方法可以是( )
A.向下平移3个单位长度
B.向上平移3个单位长度
C.向上平移2个单位长度
D.向下平移2个单位长度
5.已知二次函数y=2x2+3的图象上有三点A(,y1),B(5,y2),C(-,y3),则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y2>y3>y1
C.y1>y2>y3 D.y1>y3>y2
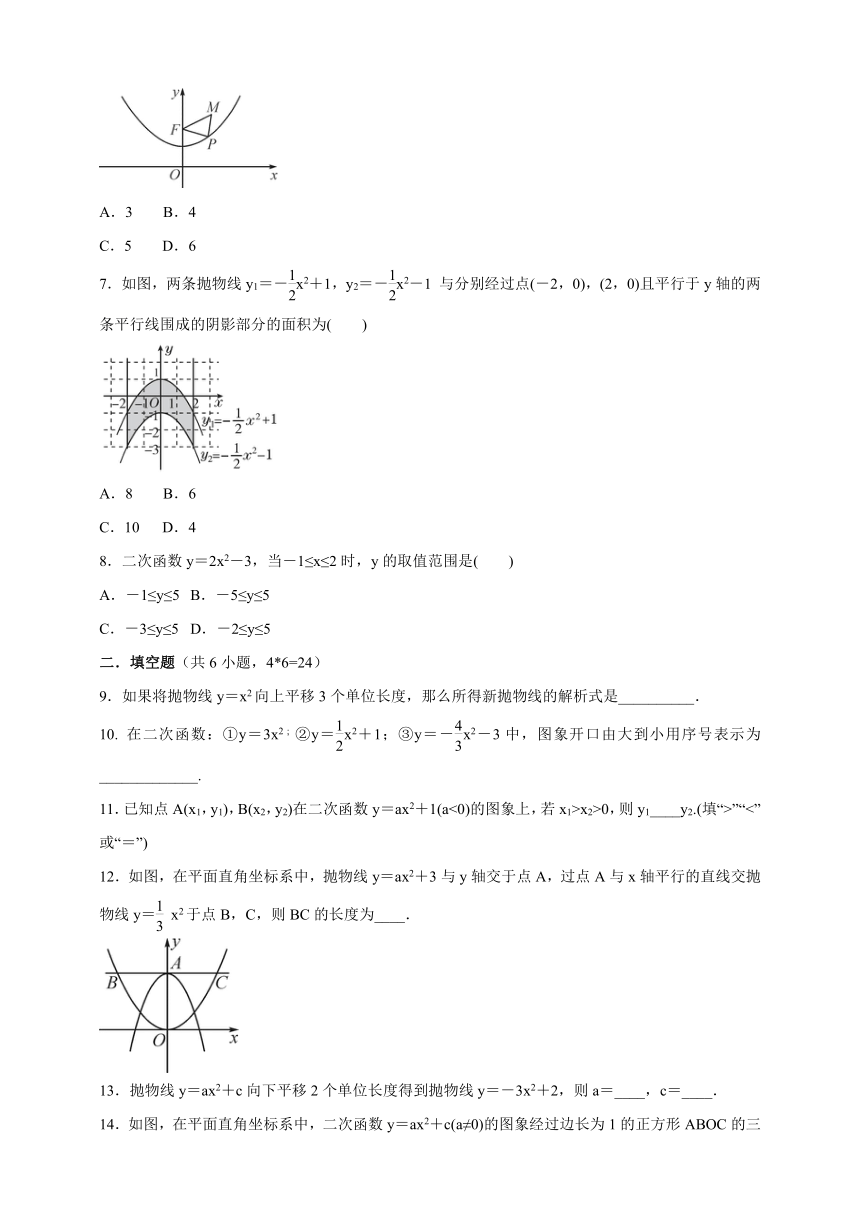
6. 已知抛物线y=x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(,3),P是抛物线y=x2+1上一个动点,则△PMF周长的最小值是( )
A.3 B.4
C.5 D.6
7.如图,两条抛物线y1=-x2+1,y2=-x2-1 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为( )
A.8 B.6
C.10 D.4
8.二次函数y=2x2-3,当-1≤x≤2时,y的取值范围是( )
A.-1≤y≤5 B.-5≤y≤5
C.-3≤y≤5 D.-2≤y≤5
二.填空题(共6小题,4*6=24)
9.如果将抛物线y=x2向上平移3个单位长度,那么所得新抛物线的解析式是__________.
10. 在二次函数:①y=3x2 ; ②y=x2+1;③y=-x2-3中,图象开口由大到小用序号表示为_____________.
11.已知点A(x1,y1),B(x2,y2)在二次函数y=ax2+1(a<0)的图象上,若x1>x2>0,则y1____y2.(填“>”“<”或“=”)
12.如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B,C,则BC的长度为____.
13.抛物线y=ax2+c向下平移2个单位长度得到抛物线y=-3x2+2,则a=____,c=____.
14.如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象经过边长为1的正方形ABOC的三个顶点A,B,C,则ac的值是___________
三.解答题(共5小题, 44分)
15.(6分) 不画图象,说出下列抛物线的对称轴、开口方向、顶点坐标及函数的最值.
(1)y=-x2+3;
(2)y=5x2-2.
16.(8分) 一个二次函数,它的图象的顶点是原点,对称轴是y轴,且经过点(-1,).
(1)求这个二次函数的表达式;
(2)画出这个二次函数的图象;
(3)指出图象的形状,当x>0时,y随x的变化情况;
(4)指出函数的最大值或最小值.
17.(8分) 已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
18.(10分) 抛物线y=2x2+n与直线y=2x-1交于点(m,3).
(1)求m和n的值;
(2)求抛物线y=2x2+n的顶点坐标和对称轴;
(3)当x取何值时,二次函数y=2x2+n中,y随x的增大而减小?
(4)函数y=2x2+n与y=2x-1的图象是否还有其他交点?若有,请求出来;若没有,请说明理由.
19.(12分) 某公园有一个形状为抛物线的观景拱桥ACB,其横截面如图所示.在图中建立直角坐标系,抛物线的表达式为y=-x2+c,且过点C(0,5).(长度单位:米)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥台阶表面铺设一条宽度为1.5米的地毯,地毯价格为20元/平方米,求购地毯要多少元?
(3)在拱桥维修加固时,搭建的“脚手架”为矩形EFGH(H,G分别在抛物线上),并铺设斜面EG.已知矩形的周长为27.5米,求G点的坐标.
参考答案
1-4CADA 5-8BCAC
9. y=x2+3 10. ②③① 11. < 12. 6 13. -3,4 14. -2
15. 解:(1)对称轴为y轴,开口向下,顶点坐标为(0,3),函数有最大值3
(2)对称轴为y轴,开口向上,顶点坐标为(0,-2),函数有最小值-2
16. 解:(1)设y=ax2,将(-1,)代入得a=,∴y=x2
(2)如图:
(3)抛物线,当x>0时,y随x的增大而增大
(4)当x=0时,有最小值为0
17. 解:(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,∴k2+k-6=0,解得k1=-3,k2=2,又∵抛物线y=x2+(k2+k-6)x+3k与x轴有两个交点,∴3k<0,∴k=-3
(2)∵点P在抛物线y=x2-9上,且P到y轴的距离是2,∴点P的横坐标为2或-2,当x=2时,y=-5,当x=-2时,y=-5.∴P(2,-5)或P(-2,-5)
18. 解:(1)m=2,n=-5
(2)抛物线的解析式为y=2x2-5,顶点坐标是(0,-5),对称轴是y轴
(3)当x<0时,y随x的增大而减小
(4)(-1,-3)
19. 解:(1)c=5
(2)令y=-x2+5=0,得x1=-10,x2=10,地毯的总长度为AB+2CO=20+2×5=30,∴需费用:30×1.5×20=900(元)
(3)设点G的坐标为(m,-m2+5),其中m>0,则EF=2m,GF=-m2+5,∴2(2m-m2+5)=27.5,解得m1=5,m2=35(舍去),将m=5代入得-m2+5=3.75,∴G点的坐标是(5,3.75)
22.1.3.1二次函数y=ax2+k的图象和性质
能力提升卷
一、选择题(共8小题,4*8=32)
1.在抛物线y=-x2+1上的一个点是( )
A.(1,0) B.(0,0)
C.(0,-1) D.(1,1)
2.抛物线y=ax2+k的顶点是(0,2),且形状及开口方向与抛物线y=-x2相同,则a,k的值分别为( )
A.-,2 B.-,-2
C.,2 D.,-2
3.二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
4.将抛物线y=2x2+3平移后得到抛物线y=2x2,平移的方法可以是( )
A.向下平移3个单位长度
B.向上平移3个单位长度
C.向上平移2个单位长度
D.向下平移2个单位长度
5.已知二次函数y=2x2+3的图象上有三点A(,y1),B(5,y2),C(-,y3),则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y2>y3>y1
C.y1>y2>y3 D.y1>y3>y2
6. 已知抛物线y=x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(,3),P是抛物线y=x2+1上一个动点,则△PMF周长的最小值是( )
A.3 B.4
C.5 D.6
7.如图,两条抛物线y1=-x2+1,y2=-x2-1 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为( )
A.8 B.6
C.10 D.4
8.二次函数y=2x2-3,当-1≤x≤2时,y的取值范围是( )
A.-1≤y≤5 B.-5≤y≤5
C.-3≤y≤5 D.-2≤y≤5
二.填空题(共6小题,4*6=24)
9.如果将抛物线y=x2向上平移3个单位长度,那么所得新抛物线的解析式是__________.
10. 在二次函数:①y=3x2 ; ②y=x2+1;③y=-x2-3中,图象开口由大到小用序号表示为_____________.
11.已知点A(x1,y1),B(x2,y2)在二次函数y=ax2+1(a<0)的图象上,若x1>x2>0,则y1____y2.(填“>”“<”或“=”)
12.如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=x2于点B,C,则BC的长度为____.
13.抛物线y=ax2+c向下平移2个单位长度得到抛物线y=-3x2+2,则a=____,c=____.
14.如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象经过边长为1的正方形ABOC的三个顶点A,B,C,则ac的值是___________
三.解答题(共5小题, 44分)
15.(6分) 不画图象,说出下列抛物线的对称轴、开口方向、顶点坐标及函数的最值.
(1)y=-x2+3;
(2)y=5x2-2.
16.(8分) 一个二次函数,它的图象的顶点是原点,对称轴是y轴,且经过点(-1,).
(1)求这个二次函数的表达式;
(2)画出这个二次函数的图象;
(3)指出图象的形状,当x>0时,y随x的变化情况;
(4)指出函数的最大值或最小值.
17.(8分) 已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值;
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
18.(10分) 抛物线y=2x2+n与直线y=2x-1交于点(m,3).
(1)求m和n的值;
(2)求抛物线y=2x2+n的顶点坐标和对称轴;
(3)当x取何值时,二次函数y=2x2+n中,y随x的增大而减小?
(4)函数y=2x2+n与y=2x-1的图象是否还有其他交点?若有,请求出来;若没有,请说明理由.
19.(12分) 某公园有一个形状为抛物线的观景拱桥ACB,其横截面如图所示.在图中建立直角坐标系,抛物线的表达式为y=-x2+c,且过点C(0,5).(长度单位:米)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥台阶表面铺设一条宽度为1.5米的地毯,地毯价格为20元/平方米,求购地毯要多少元?
(3)在拱桥维修加固时,搭建的“脚手架”为矩形EFGH(H,G分别在抛物线上),并铺设斜面EG.已知矩形的周长为27.5米,求G点的坐标.
参考答案
1-4CADA 5-8BCAC
9. y=x2+3 10. ②③① 11. < 12. 6 13. -3,4 14. -2
15. 解:(1)对称轴为y轴,开口向下,顶点坐标为(0,3),函数有最大值3
(2)对称轴为y轴,开口向上,顶点坐标为(0,-2),函数有最小值-2
16. 解:(1)设y=ax2,将(-1,)代入得a=,∴y=x2
(2)如图:
(3)抛物线,当x>0时,y随x的增大而增大
(4)当x=0时,有最小值为0
17. 解:(1)∵抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,∴k2+k-6=0,解得k1=-3,k2=2,又∵抛物线y=x2+(k2+k-6)x+3k与x轴有两个交点,∴3k<0,∴k=-3
(2)∵点P在抛物线y=x2-9上,且P到y轴的距离是2,∴点P的横坐标为2或-2,当x=2时,y=-5,当x=-2时,y=-5.∴P(2,-5)或P(-2,-5)
18. 解:(1)m=2,n=-5
(2)抛物线的解析式为y=2x2-5,顶点坐标是(0,-5),对称轴是y轴
(3)当x<0时,y随x的增大而减小
(4)(-1,-3)
19. 解:(1)c=5
(2)令y=-x2+5=0,得x1=-10,x2=10,地毯的总长度为AB+2CO=20+2×5=30,∴需费用:30×1.5×20=900(元)
(3)设点G的坐标为(m,-m2+5),其中m>0,则EF=2m,GF=-m2+5,∴2(2m-m2+5)=27.5,解得m1=5,m2=35(舍去),将m=5代入得-m2+5=3.75,∴G点的坐标是(5,3.75)
同课章节目录
