23.2.1 中心对称自学自测 2021--2022学年人教版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 23.2.1 中心对称自学自测 2021--2022学年人教版数学九年级上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 556.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览



文档简介
23.2.1 中心对称自学自测
一、选择题
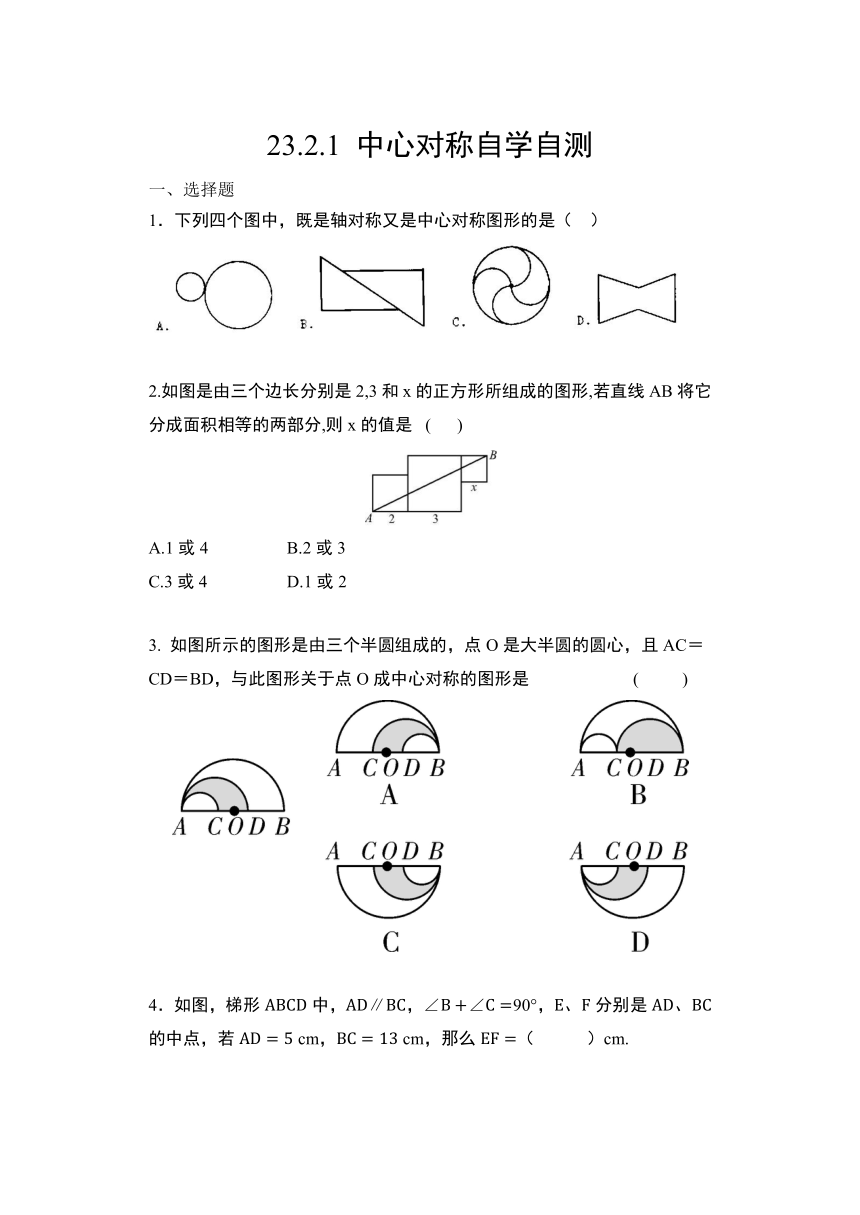
1.下列四个图中,既是轴对称又是中心对称图形的是( )
2.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是 ( )
A.1或4 B.2或3
C.3或4 D.1或2
3. 如图所示的图形是由三个半圆组成的,点O是大半圆的圆心,且AC=CD=BD,与此图形关于点O成中心对称的图形是 ( )
4.如图,梯形ABCD中,AD∥BC,∠B+∠C=90°,E、F分别是AD、BC的中点,若AD=5 cm,BC=13 cm,那么EF=( )cm.
A.4 B.5 C.6.5 D.9
5.若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是( )
A.AB=CD B.AB∥CD
C.AB平行且等于CD D.不确定
6. 下列各组图形中,△A′B′C′与△ABC成中心对称的是
( )
7.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为( )
A.4 B.false
C.false D.false
8.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,点F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
9. 如图,将△ABC绕边AC的中点O顺时针旋转180°.小淇发现,旋转后的△CDA与△ABC构成平行四边形,并有如下的推理:
小明为保证小淇的推理更严谨,想在方框中“∵AB=CD.”和“∴四边形…”之间作补充,下列正确的是 ( )
A.小淇推理严谨,不必补充
B.应补充:且CB=AD
C.应补充:且CB∥AD
D.应补充:且OA=OC
10.已知点P关于x轴的对称点P1的坐标是(4,3),那么点P关于原点的对称点P2的坐标是()
A.(-3,-4) B.(-4,3)
C.(-4,-3) D.(4,-3)
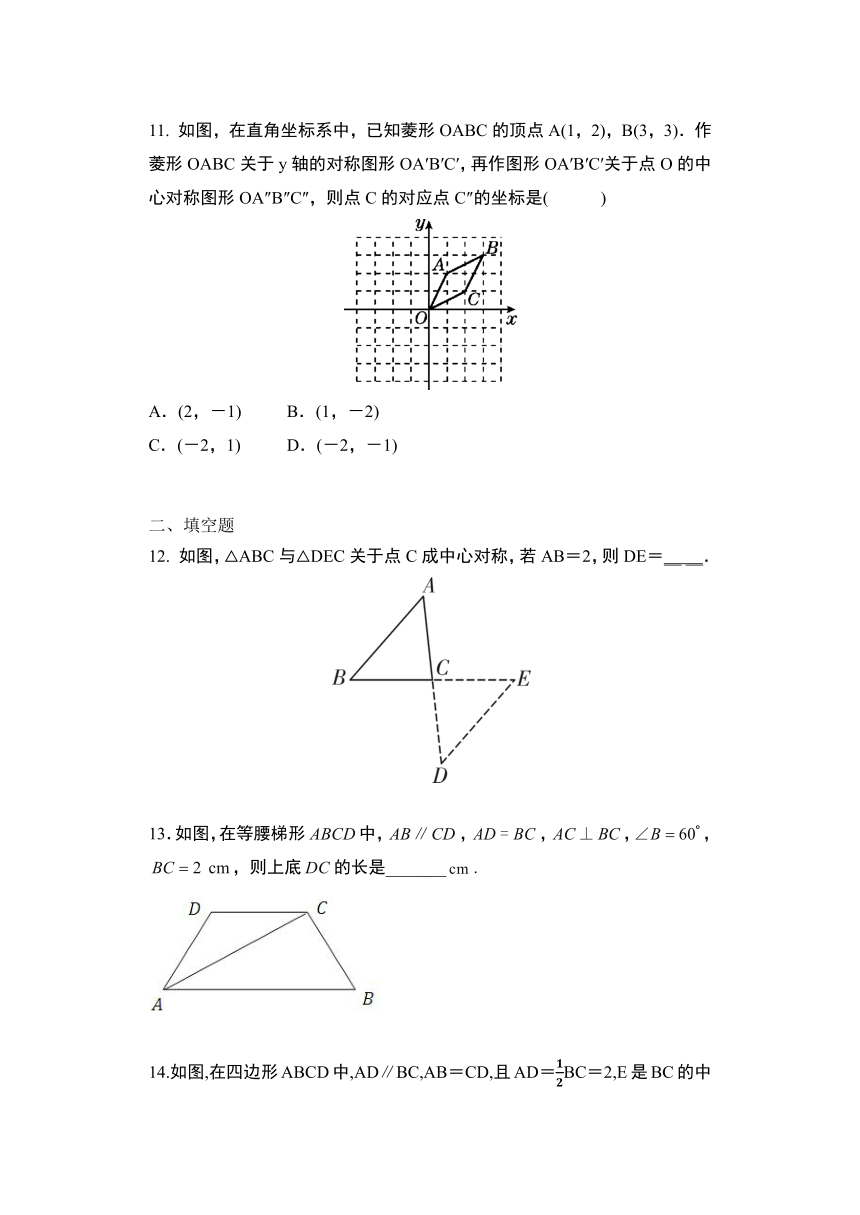
11. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
二、填空题
12. 如图,△ABC与△DEC关于点C成中心对称,若AB=2,则DE=__ __.
13.如图,在等腰梯形false中,false,false,falseAC⊥BC,false,falseBC=2 cm ,则上底false的长是_______falsecm..
14.如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=12BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 .?
15. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,……,如此作下去,则△B2 020A2 021B2 021的顶点A2 021的坐标是__ _.
三、解答题
16.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
①把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
②以原点O为对称中心,画出△ABC与关于原点对称的△A2B2C2,并写出点C2的坐标;
17.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
18. 如图,矩形ABCD和矩形AEFG关于点A成中心对称.
(1)四边形BDEG是菱形吗?请说明理由;
(2)若矩形ABCD面积为8,求四边形BDEG的面积.
19.如图,两个半圆分别以P、Q为圆心,它们的半径相等,A1、P、B1、B2、Q、A2在同一条直线上.这个图形中的两个半圆是否成中心对称?如果是,请找出对称中心O.
20.如图,在△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求△ABC的面积
(2)当∠ACB为多少度时,四边形ABFE为矩形?并说明理由.
21.如图,正方形false与正方形false关于点false中心对称,若正方形false的边长为1,设图形重合部分的面积为false,线段false的长为false,求false与false之间的函数关系式.
答案
一、选择题
1. D 2. D 3. C 4. A 5. C 6. D
7. A 8. D 9. B 10. B 11. A
二、填空题
12. 2 13. 2 14. 2 DE的中点 15. (4041, )
三、解答题
16. (1)如图所示C1(4,4);(2)如图所示C2(﹣4,﹣4).
17.解:如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
18. (1) 解:四边形BDEG是菱形.理由:∵矩形ABCD和矩形AEFG关于点A中心对称,∴AB=AE,AD=AG,BE⊥DG,
∴BD2=DE2=EG2=GB2=AB2+AD2,
∴四边形BDEG是菱形.
(2) 解:若矩形ABCD面积为8,则
S△ABD=S四边形ABCD=4,
∴根据菱形性质,四边形BDEG的面积为
SBDEG=4S△ABD=16.
19.
20.(1)解:∵△ABC与△FEC关于点C成中心对称,
∴点A,C,F共线,点B,C,E共线,AC=FC,BC=EC.
∴四边形ABFE是平行四边形.
∴S△ABC=S?ABFE=6.
(2)解:当∠ACB=60°时,四边形ABFE是矩形.理由如下:
∵AC=AB,∠ACB=60°,∴△ABC是等边三角形.
∴AC=BC.
又∵AC=CF=AF,BC=EC=BE,∴AF=BE.
又∵四边形ABFE是平行四边形,∴?ABFE是矩形.
21. false.
一、选择题
1.下列四个图中,既是轴对称又是中心对称图形的是( )
2.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是 ( )
A.1或4 B.2或3
C.3或4 D.1或2
3. 如图所示的图形是由三个半圆组成的,点O是大半圆的圆心,且AC=CD=BD,与此图形关于点O成中心对称的图形是 ( )
4.如图,梯形ABCD中,AD∥BC,∠B+∠C=90°,E、F分别是AD、BC的中点,若AD=5 cm,BC=13 cm,那么EF=( )cm.
A.4 B.5 C.6.5 D.9
5.若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是( )
A.AB=CD B.AB∥CD
C.AB平行且等于CD D.不确定
6. 下列各组图形中,△A′B′C′与△ABC成中心对称的是
( )
7.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为( )
A.4 B.false
C.false D.false
8.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,点F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
9. 如图,将△ABC绕边AC的中点O顺时针旋转180°.小淇发现,旋转后的△CDA与△ABC构成平行四边形,并有如下的推理:
小明为保证小淇的推理更严谨,想在方框中“∵AB=CD.”和“∴四边形…”之间作补充,下列正确的是 ( )
A.小淇推理严谨,不必补充
B.应补充:且CB=AD
C.应补充:且CB∥AD
D.应补充:且OA=OC
10.已知点P关于x轴的对称点P1的坐标是(4,3),那么点P关于原点的对称点P2的坐标是()
A.(-3,-4) B.(-4,3)
C.(-4,-3) D.(4,-3)
11. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
二、填空题
12. 如图,△ABC与△DEC关于点C成中心对称,若AB=2,则DE=__ __.
13.如图,在等腰梯形false中,false,false,falseAC⊥BC,false,falseBC=2 cm ,则上底false的长是_______falsecm..
14.如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=12BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 .?
15. 在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,……,如此作下去,则△B2 020A2 021B2 021的顶点A2 021的坐标是__ _.
三、解答题
16.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
①把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
②以原点O为对称中心,画出△ABC与关于原点对称的△A2B2C2,并写出点C2的坐标;
17.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
18. 如图,矩形ABCD和矩形AEFG关于点A成中心对称.
(1)四边形BDEG是菱形吗?请说明理由;
(2)若矩形ABCD面积为8,求四边形BDEG的面积.
19.如图,两个半圆分别以P、Q为圆心,它们的半径相等,A1、P、B1、B2、Q、A2在同一条直线上.这个图形中的两个半圆是否成中心对称?如果是,请找出对称中心O.
20.如图,在△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求△ABC的面积
(2)当∠ACB为多少度时,四边形ABFE为矩形?并说明理由.
21.如图,正方形false与正方形false关于点false中心对称,若正方形false的边长为1,设图形重合部分的面积为false,线段false的长为false,求false与false之间的函数关系式.
答案
一、选择题
1. D 2. D 3. C 4. A 5. C 6. D
7. A 8. D 9. B 10. B 11. A
二、填空题
12. 2 13. 2 14. 2 DE的中点 15. (4041, )
三、解答题
16. (1)如图所示C1(4,4);(2)如图所示C2(﹣4,﹣4).
17.解:如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
18. (1) 解:四边形BDEG是菱形.理由:∵矩形ABCD和矩形AEFG关于点A中心对称,∴AB=AE,AD=AG,BE⊥DG,
∴BD2=DE2=EG2=GB2=AB2+AD2,
∴四边形BDEG是菱形.
(2) 解:若矩形ABCD面积为8,则
S△ABD=S四边形ABCD=4,
∴根据菱形性质,四边形BDEG的面积为
SBDEG=4S△ABD=16.
19.
20.(1)解:∵△ABC与△FEC关于点C成中心对称,
∴点A,C,F共线,点B,C,E共线,AC=FC,BC=EC.
∴四边形ABFE是平行四边形.
∴S△ABC=S?ABFE=6.
(2)解:当∠ACB=60°时,四边形ABFE是矩形.理由如下:
∵AC=AB,∠ACB=60°,∴△ABC是等边三角形.
∴AC=BC.
又∵AC=CF=AF,BC=EC=BE,∴AF=BE.
又∵四边形ABFE是平行四边形,∴?ABFE是矩形.
21. false.
同课章节目录
