22.3实际问题与二次函数(图形运动问题)课后培优习题 2021-2022学年九年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 22.3实际问题与二次函数(图形运动问题)课后培优习题 2021-2022学年九年级数学人教版上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 943.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览

文档简介
1083310012458700实际问题与二次函数——图形运动问题
一、单选题
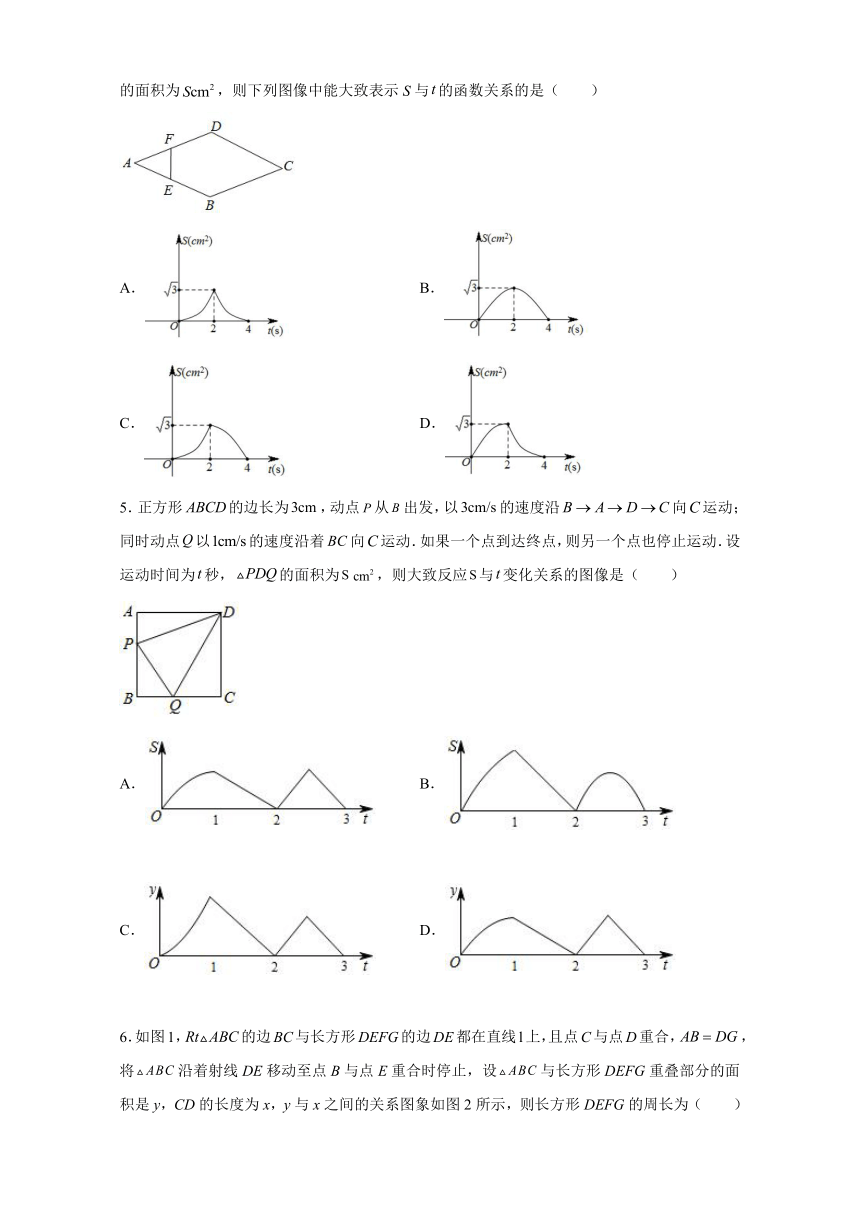
1.如图,正方形false和等腰直角三角形false,斜边false与false在一条直线上,false沿射线false方向运动(点E从点D出发),设false与正方形false重叠部分的面积为y.若false,则x的值为( )
A.false或false B.false或false C.false或false D.false或false
2.如图,点false是菱形false边上的动点,它从点false出发沿false路径匀速运动到点false,设false的面积为false,点false的运动时间为false,则false关于false的函数图象大致为( )
A. B. C. D.
3.如图,在平面直角坐标系中,点false的坐标为false,点false在直线false上运动,设false的面积为false,则下列图象中,能反映false与false的函数关系的是( ).
A.B.C. D.
4.如图,菱形false的边长为false,其中false,动点false同时从点A都以false的速度出发,点false沿false路线,点false沿false路线运动.连接false.设运动时间为false,false的面积为false,则下列图像中能大致表示S与false的函数关系的是( )
A. B.
C. D.
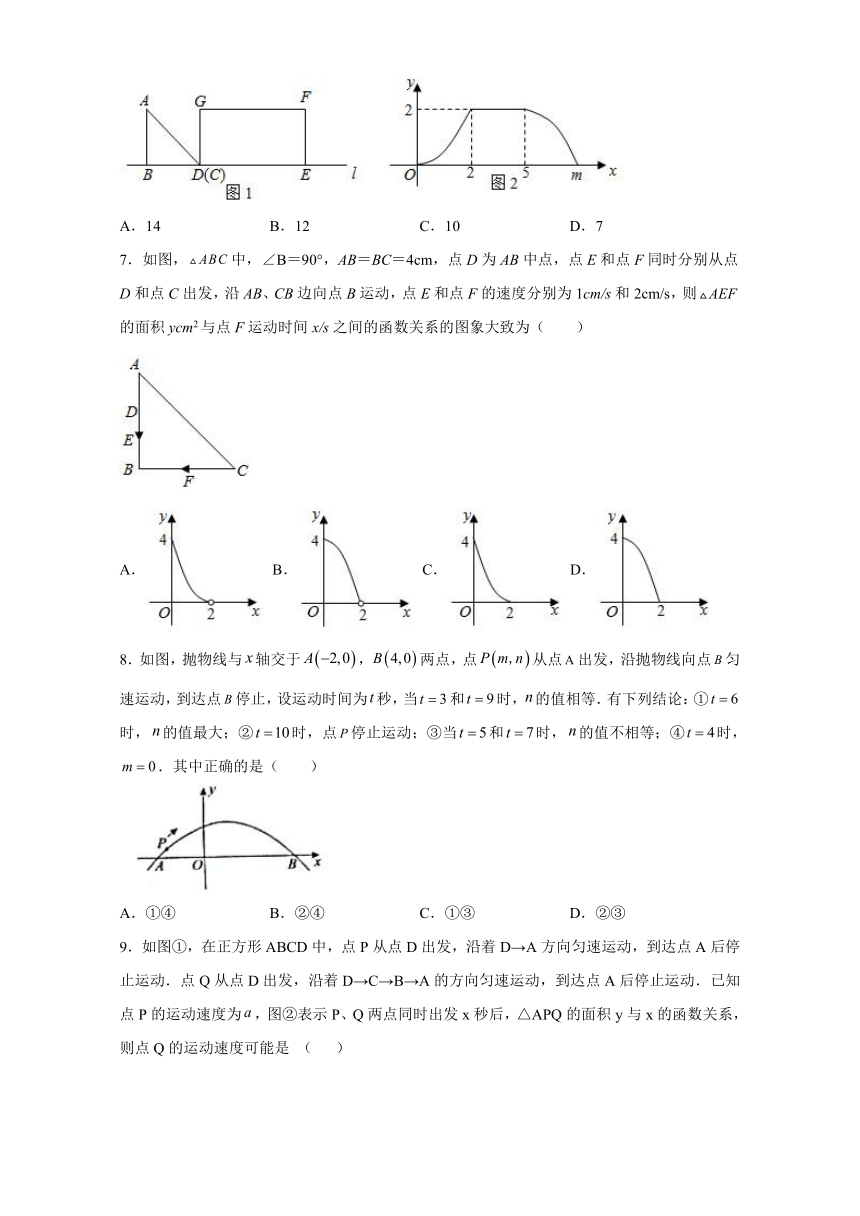
5.正方形false的边长为false,动点false从false出发,以false的速度沿false向false运动;同时动点false以false的速度沿着false向false运动.如果一个点到达终点,则另一个点也停止运动.设运动时间为false秒,false的面积为falsefalse,则大致反应false与false变化关系的图像是( )
A. B.
C. D.
6.如图1,false的边BC与长方形DEFG的边DE都在直线l上,且点C与点D重合,false,将false沿着射线DE移动至点B与点E重合时停止,设false与长方形DEFG重叠部分的面积是y,CD的长度为x,y与x之间的关系图象如图2所示,则长方形DEFG的周长为( )
A.14 B.12 C.10 D.7
7.如图,false中,∠B=90°,AB=BC=4cm,点D为AB中点,点E和点F同时分别从点D和点C出发,沿AB、CB边向点B运动,点E和点F的速度分别为1cm/s和2cm/s,则false的面积ycm2与点F运动时间x/s之间的函数关系的图象大致为( )
A. B. C. D.
8.如图,抛物线与false轴交于false,false两点,点false从点false出发,沿抛物线向点false匀速运动,到达点false停止,设运动时间为false秒,当false和false时,false的值相等.有下列结论:①false时,false的值最大;②false时,点false停止运动;③当false和false时,false的值不相等;④false时,false.其中正确的是( )
A.①④ B.②④ C.①③ D.②③
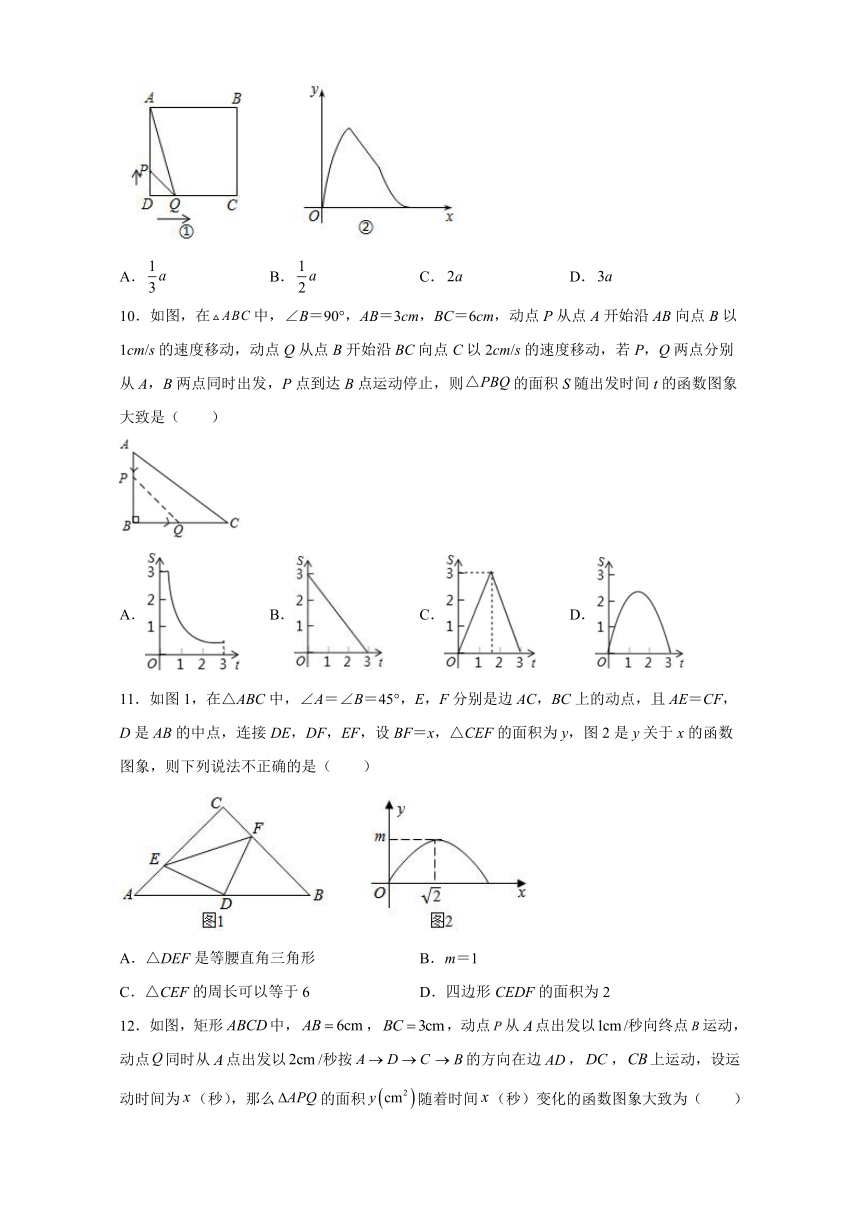
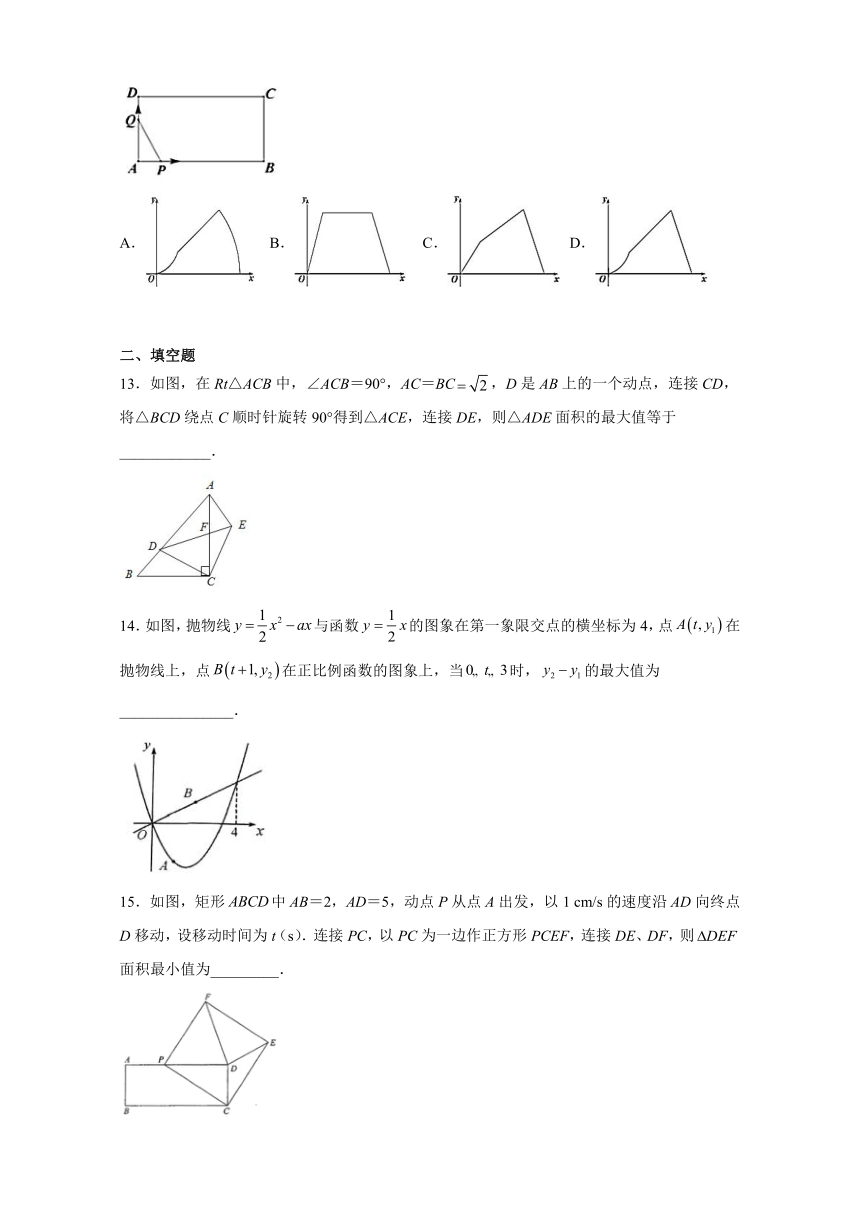
9.如图①,在正方形ABCD中,点P从点D出发,沿着D→A方向匀速运动,到达点A后停止运动.点Q从点D出发,沿着D→C→B→A的方向匀速运动,到达点A后停止运动.已知点P的运动速度为false,图②表示P、Q两点同时出发x秒后,△APQ的面积y与x的函数关系,则点Q的运动速度可能是 ( )
A.false B.false C.false D.false
10.如图,在false中,∠B=90°,AB=3cm,BC=6cm,动点P从点A开始沿AB向点B以1cm/s的速度移动,动点Q从点B开始沿BC向点C以2cm/s的速度移动,若P,Q两点分别从A,B两点同时出发,P点到达B点运动停止,则false的面积S随出发时间t的函数图象大致是( )
A. B. C. D.
11.如图1,在△ABC中,∠A=∠B=45°,E,F分别是边AC,BC上的动点,且AE=CF,D是AB的中点,连接DE,DF,EF,设BF=x,△CEF的面积为y,图2是y关于x的函数图象,则下列说法不正确的是( )
A.△DEF是等腰直角三角形 B.m=1
C.△CEF的周长可以等于6 D.四边形CEDF的面积为2
12.如图,矩形false中,false,false,动点false从false点出发以false/秒向终点false运动,动点false同时从false点出发以false/秒按falsefalse的方向在边false,false,false上运动,设运动时间为false(秒),那么false的面积false随着时间false(秒)变化的函数图象大致为( )
B. C. D.
二、填空题
13.如图,在Rt△ACB中,∠ACB=90°,AC=BCfalse,D是AB上的一个动点,连接CD,将△BCD绕点C顺时针旋转90°得到△ACE,连接DE,则△ADE面积的最大值等于____________.
14.如图,抛物线false与函数false的图象在第一象限交点的横坐标为4,点false在抛物线上,点false在正比例函数的图象上,当false时,false的最大值为_______________.
15.如图,矩形false中AB=2,AD=5,动点P从点A出发,以1 cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则false面积最小值为_________.
16.如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始向B点以2cm/s的速度移动(不与点B重合);动点Q从点B开始向点C以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过_____秒四边形APQC的面积最小.
17.如图,在false中,false,false,false为false边上的高,动点false在false上,从点false出发,沿false方向运动,设false,false的面积为false,矩形false的面积为false,false,则false与false的关系式是________.
三、解答题
18.如图,正方形false的边长为false,false,false分别是false,false边上一动点,点false,false同时从点false出发,以每秒false的速度分别向点false,false运动,当点false与点false重合时,运动停止,设运动时间为false,运动过程中false的面积为false,求false关于false的函数表达式,并写出自变量false的取值范围.
19.如图,抛物线false经过false,false两点,点false是false轴左侧且位于false轴下方抛物线上一动点,设其横坐标为false.
(1)直接写出抛物线的解析式;
(2)将线段false绕点false顺时针旋转false得线段false(点false是点false的对应点),求点false的坐标,并判断点D是否在抛物线上;
(3)过点false作false轴交直线false于点false,试探究是否存在点false,使false是等腰三角形?若存在,求出点false的值;若不存在,说明理由.
20.如图,在矩形ABCD中,AB=4,AD=2.点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x秒,△APQ的面积为S(平方单位).
(1)点P、Q从出发到相遇所用的时间是 秒.
(2)当2<x≤3时,求S与x之间的函数关系式 .
(3)当(2)的条件下,x为何值时,△APQ的面积为false.
21.在平面直角坐标系xOy中,抛物线y=﹣x2+2tx+2.
(1)求抛物线的对称轴(用含t的代数式表示);
(2)将点A(﹣1,3)向右平移5个单位长度,得到点B.
①若抛物线经过点B求t的值;
②若抛物线与线段AB恰有一个交点,结合函数图象直接写出t的取值范围.
22.如图,抛物线false与直线false相交于false,false两点,且抛物线经过点false
(1)求抛物线的解析式;
(2)点P是抛物线上的一个动点(不与点A.点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.当PE=2ED时,求P点坐标;
(3)点P是直线上方的抛物线上的一个动点,求false的面积最大时的P点坐标.
参考答案
1.B
解:有题意可知,false沿射线false运动的过程中,重叠面积y是先增加,然后不变,然后减小,最后为0
当false时,false,此时false,false无解;
当false时,false,令false,解得false;
当false时,false,false无解;
当false时,false,令false,解得false;
当false时,false,false无解;
综上所述,false或false
故答案选B.
2.C
解:设菱形的高为h,分三种情况:
①当P在BC边上时,
y=falseBP?h,
∵BP随x的增大而增大,h不变,
∴y随x的增大而增大,且为一次函数关系,
故选项A和D不正确;
②当P在边DC上时,
y=falseAB?h,
AB和h都不变,
∴在这个过程中,y不变,
故选项B不正确;
③当P在边AD上时,
y=falseAP?h,
∵PA随x的增大而减小,h不变,
∴y随x的增大而减小,且为一次函数,
故选:C;
3.C
解:∵点P(m,n)在直线y=?x+2上运动,
∴当m=1时,n=1,即P点在直线AO上,此时S=0,
设直线false与y轴交于点B,则B(0,2),连接AB,
∵点A的坐标为false,B(0,2),
∴false是等腰直角三角形,且false,
当m≤1时,S△APO=false×2×2-false×2×m×2=2?2m,
∴S与m是一次函数关系,
同理:当m>1时,S△APO=2m?2,故S与m是一次函数关系,
只有选项C符合题意.
故选:C.
4.C
解:false,
当点E在AB上运动时,即false时,
∵动点false同时从点A都以false的速度出发,
false.
false,
false为等边三角形,
false,
∴图象为开口向上的抛物线;
当点E在BC上运动时,即false时,此时false,
false.
∵四边形ABCD是菱形,
false,
false,
false为等边三角形,
false,
false,
false,
false,
false,
false,
∴图象为开口向下的抛物线,
综上所述,C选项符合题意,
故选:C.
5.B
解:①当点P在AB上运动时,则PB=3t,BQ=t,
则AP=3-3t,CQ=3-t,
S=S正方形ABCD-S△PBQ-S△ADP-S△CDQ=3×3-false[t?3t+(3-3t)×3+3(3-t)]=-falset2+6t,
该函数为开口向下的抛物线;
②当点P在AD上运动时,
则S=false×PD×AB=false×(3t-3)=falset-false;
③当点P在CD上运动时,
同理可得S=-false(t-2)(t-3)为开口向下的抛物线;
故选:B.
6.A
解:从图2看,false向右平移2个单位时,false整体到长方体中了,此时false与长方形DEFG重叠部分的面积为false的面积为false且false,
falsefalse的面积为false,
解得:false,
false.
false再向右平移3个单位时,点false重合,
故:false,
false长方形false的周长为false,
故选:A.
7.D
解:由题意得:设CF=2x,DE=x,
则BF=BC﹣FC=4﹣2x,AE=AD+DE=2+x,
则y=falseAE×BF=false×(2+x)(4﹣2x)=﹣x2+4(0≤x≤2),
故选:D.
8.A
解:过点P作PQ⊥x轴于Q,
根据题意,该抛物线的对称轴是直线x=false =1.设点Q的运动速度是每秒v个单位长度,
则∵当t=3和t=9时,n的值相等,
∴x=false[(9v?2)+(3v?2)] =1,
∴v=false .
①当t=6时,AQ=6×false =3,此时点P是抛物线顶点坐标,即n的值最大,故结论正确;
②当t=10时,AQ=10×false =5,此时点Q与点B不重合,即n≠0,故结论错误;
③当t=5时,AQ=false,此P时点的坐标是(false ,0);
当t=7时,AQ=false,此时点P的坐标是(false,0).
因为点(false,0)与点(false,0)关于对称轴直线x=1对称,所以n的值一定相等,故结论错误;
④t=4时,AQ=4×false=2,此时点Q与原点重合,则m=0,故结论正确.
综上所述,正确的结论是①④.
故选:A.
9.D
解:观察图象,可以发现函数图象由三个阶段构成,即△APQ的顶点Q所在边应有三种可能.
当Q的速度低于点P时,当点P到达A时,点Q还在DC上运动,之后,因A、P重合,△APQ的面积为零,画出图象只能有一个阶段构成,故A、B错误;
当Q的速度是点P速度的2倍,当点P到点A时,点Q到点B.之后,点A、P重合,△APQ的面积为0.
期间△APQ面积的变化可以看成两个阶段,与图象不符,故C错误.
故选:D.
10.D
解:设运动时间为false,
false点P到达点B所需时间为false,点Q到达点C所需时间为false,
false点P、Q同时停止运动,且false的取值范围为false,
由题意,false,
false,
false,
false,
则false与false之间的函数图象是抛物线在false的部分,且开口向下,
观察四个选项可知,只有选项D符合,
故选:D.
11.C
解:A.连接CD,
∵△ABC为等腰直角三角形,D是AB的中点,
∴CD=AD=BD,∠DCF=∠A=45°
而AE=CF,
∴△ADE≌△CDF(SAS),
∴DF=DE,∠CDF=∠ADE,
∴∠EDF=∠EDC+∠CDF=∠CDE+∠EDA=90°,CE=BF,
∴△DEF是等腰直角三角形,
故A正确;
B.设AC=BC=a,CE=BF=a﹣x,
S△CFE=false×CE×CF=falsex(a﹣x),
当x=falsea=false时,S△CFE有最大值=false×false×(2false﹣false)=1,
故m=1,此时a=4false,
故B正确;
C.△CEF的周长=EC+CF+EF=AC+EF=2false+EF,
而EF<CE+CF=2false,
即△CEF的周长=EC+CF+EF=AC+EF=2false+EF<4false<6,
故C错误;
D.四边形CEDF的面积=S△CDE+S△CDF=S△CDE+S△AED=S△ACD=falseS△ABC=false×false×2false×2false=2,
故D正确.
故选:C.
12.A
解:根据题意可知:AP=x,Q点运动路程为2x,
①当点Q在AD上运动时,
y=falseAP?AQ=falsex?2x=x2,图象为开口向上的二次函数;
②当点Q在DC上运动时,
y=falseAP?DA=falsex×3=false,是一次函数;
③当点Q在BC上运动时,
y=falseAP?BQ=falsex?(12?2x)=?x2+6x,为开口向下的二次函数,
结合图象可知A选项函数关系图正确,
故选:A.
13.false
解:如图,△BCD绕点C顺时针旋转90°得到△ACE,
∴△BDC≌△AEC,
∴∠B=∠CAE,
∵BC=AC=false,△ABC为等腰直角三角形,
∴∠B=∠CAE=∠BAC=45°,
∴∠DAE=∠BAC+∠CAE=90°,
在Rt△ABC中,由勾股定理AB=false,
设BD=AE=x,则AD=(2-x),
∴false,
∵false,函数开口向下,函数有最大值,
当x=1时,false.
故答案为:false.
14.false
解:把x=4代入false得y=2
把x=4,y=2代入false得false
解得a=false
∴false
当x=t时,false,当x=t+1时,false
∴当false时,false=false=false=false
∵false<0,
∴当t=2时,false的最大值为false
故答案为:false.
15.false
解:由题意得:AP=t,PD=5-t,
∴false,
∵四边形PCEF是正方形,
∴false,
∵false,
∴false,
∴false,
∴当t=4时,△DEF的面积最小,最小值为false.
故答案为:false.
16.3
解:设运动时间为t秒时(0≤t≤6),四边形APQC的面积为S,
∵PB=AB﹣2t=12﹣2t,BQ=4t,
∴S△BPQ=falsePB?BQ=false(12﹣2t)?4t=24t﹣4t2,
∴S=S△ABC﹣S△BPQ=falseAB?BC﹣(24t﹣4t2)=4t2﹣24t+144,
∵S=4t2﹣24t+144=4(t﹣3)2+108,
∴经过3秒四边形APQC的面积最小,
故答案为:3.
17.false
解:在false中,false,false,
∴false,
∵false为false边上的高,
∴AD=BD=DC=false
设false,
∴PD=false,
∵矩形false,由于DF在BC上,
∴PE∥DC,
∴∠AEP=∠C=∠DAC=45?,
∴PE=AP=x,
S1=false,
S2=false,
∴false,
false.
故答案为:false.
18.falsefalse
解:设运动时间为false,
false点false,false同时从点false出发,以每秒false的速度分别向点false,false运动,
false,false,false,false,
false的面积false正方形false的面积false的面积false的面积false的面积,
即:false
false
false false
19.(1)false;(2)false,点false不在抛物线上;(3)存在点false,使false是等腰三角形,false的值为false或false或false
解:(1)将false,false两点的坐标代入false得
false
解得false
∴抛物线的解析式为:
false
false作false轴于点false轴于点false,如下图,
则false
易证false
false
false
false
将x=-3代入false得
false,
∵false
false点false不在抛物线上.
false过点false作false轴交false于点false,
设直线false解析式为false,
则false,
解得false
false直线false解析式为false.
依题意false
false当false时,则false
false
解得false(舍去),false;
false当false时,则false,
解得false(舍去),false
false当false时,
false
false
false
false轴,
false点false的纵坐标为false
false,
解得false(舍去),false.
综上所述:存在点false,使false是等腰三角形,
false的值为false或false或false.
20.(1)4;(2)S=﹣x2+4x;(3)满足条件的x的值为2+false.
解:(1)(4×2+2×2)÷(2+1)=4(秒),
故答案为4.
(2)如图,当2<x≤3时,点P在线段BC上,点Q在线段CD上,
∴S=S矩形ABCD﹣S△ADQ﹣S△ABP﹣S△CPQ=4×2﹣false×2×(x﹣2)﹣false×4×(2x﹣4)﹣false×(6﹣x)×(6﹣2x)=﹣x2+4x.
故答案为:S=﹣x2+4x.
(3)当2<x≤3时,﹣x2+4x=false,
∴x=2±false,
∵2<x≤3,
∴x=2+false.
∴满足条件的x的值为2+false.
21.(1)直线x=t;(2)①t=false;②t≤﹣1或t=1或t>false时,抛物线与线段AB有一个公共点.
解:(1)∵抛物线y=﹣x2+2tx+2,
∴抛物线的对称轴为直线x=﹣false=t,
即抛物线的对称轴为直线x=t;
(2)点A(﹣1,3)向右平移5个长度单位,得到点B(4,3),
①∵抛物线经过点B,
∴3=﹣16+8t+2,
解得t=false;
②∵y=﹣x2+2tx+2=﹣(x﹣t)2+t2+2,
∴顶点的坐标为(t,t2+2),
由顶点的坐标可知,抛物线的顶点在抛物线y=x2+2上移动.
把y=3代入y=x2+2求得x=±1,
当抛物线过点A(﹣1,3)时,t=﹣1.
所以t≤﹣1或t=1或t>false时,抛物线与线段AB有一个公共点.
22.(1)y=?x2+4x+5(2)P点坐标为(2,9)或(6,?7);(3)P(false,false).
解:(1)∵点B(4,m)在直线y=x+1上,
∴m=4+1=5,
∴B(4,5),
把A、B、C三点坐标代入抛物线解析式可得
false,
解得
false,
∴抛物线解析式为y=?x2+4x+5;
(2)设P(x,?x2+4x+5),则E(x,x+1),D(x,0),
则PE=|?x2+4x+5?(x+1)|=|?x2+3x+4|,DE=|x+1|,
∵PE=2ED,
∴|?x2+3x+4|=2|x+1|,
当?x2+3x+4=2(x+1)时,解得x=?1或x=2,但当x=?1时,P与A重合不合题意,舍去,
∴P(2,9);
当?x2+3x+4=?2(x+1)时,解得x=?1或x=6,但当x=?1时,P与A重合不合题意,舍去,
∴P(6,?7);
综上可知P点坐标为(2,9)或(6,?7);
(3)∵点P是直线上方的抛物线上的一个动点,
设(x,?x2+4x+5),则E(x,x+1),D(x,0),
则PE=?x2+4x+5?(x+1)=?x2+3x+4,
∴false= Sfalse+ Sfalse=false=false
=false
∴当x=false,false的面积最大
把x=false代入y=?x2+4x+5,解得y=false
故P(false,false).
一、单选题
1.如图,正方形false和等腰直角三角形false,斜边false与false在一条直线上,false沿射线false方向运动(点E从点D出发),设false与正方形false重叠部分的面积为y.若false,则x的值为( )
A.false或false B.false或false C.false或false D.false或false
2.如图,点false是菱形false边上的动点,它从点false出发沿false路径匀速运动到点false,设false的面积为false,点false的运动时间为false,则false关于false的函数图象大致为( )
A. B. C. D.
3.如图,在平面直角坐标系中,点false的坐标为false,点false在直线false上运动,设false的面积为false,则下列图象中,能反映false与false的函数关系的是( ).
A.B.C. D.
4.如图,菱形false的边长为false,其中false,动点false同时从点A都以false的速度出发,点false沿false路线,点false沿false路线运动.连接false.设运动时间为false,false的面积为false,则下列图像中能大致表示S与false的函数关系的是( )
A. B.
C. D.
5.正方形false的边长为false,动点false从false出发,以false的速度沿false向false运动;同时动点false以false的速度沿着false向false运动.如果一个点到达终点,则另一个点也停止运动.设运动时间为false秒,false的面积为falsefalse,则大致反应false与false变化关系的图像是( )
A. B.
C. D.
6.如图1,false的边BC与长方形DEFG的边DE都在直线l上,且点C与点D重合,false,将false沿着射线DE移动至点B与点E重合时停止,设false与长方形DEFG重叠部分的面积是y,CD的长度为x,y与x之间的关系图象如图2所示,则长方形DEFG的周长为( )
A.14 B.12 C.10 D.7
7.如图,false中,∠B=90°,AB=BC=4cm,点D为AB中点,点E和点F同时分别从点D和点C出发,沿AB、CB边向点B运动,点E和点F的速度分别为1cm/s和2cm/s,则false的面积ycm2与点F运动时间x/s之间的函数关系的图象大致为( )
A. B. C. D.
8.如图,抛物线与false轴交于false,false两点,点false从点false出发,沿抛物线向点false匀速运动,到达点false停止,设运动时间为false秒,当false和false时,false的值相等.有下列结论:①false时,false的值最大;②false时,点false停止运动;③当false和false时,false的值不相等;④false时,false.其中正确的是( )
A.①④ B.②④ C.①③ D.②③
9.如图①,在正方形ABCD中,点P从点D出发,沿着D→A方向匀速运动,到达点A后停止运动.点Q从点D出发,沿着D→C→B→A的方向匀速运动,到达点A后停止运动.已知点P的运动速度为false,图②表示P、Q两点同时出发x秒后,△APQ的面积y与x的函数关系,则点Q的运动速度可能是 ( )
A.false B.false C.false D.false
10.如图,在false中,∠B=90°,AB=3cm,BC=6cm,动点P从点A开始沿AB向点B以1cm/s的速度移动,动点Q从点B开始沿BC向点C以2cm/s的速度移动,若P,Q两点分别从A,B两点同时出发,P点到达B点运动停止,则false的面积S随出发时间t的函数图象大致是( )
A. B. C. D.
11.如图1,在△ABC中,∠A=∠B=45°,E,F分别是边AC,BC上的动点,且AE=CF,D是AB的中点,连接DE,DF,EF,设BF=x,△CEF的面积为y,图2是y关于x的函数图象,则下列说法不正确的是( )
A.△DEF是等腰直角三角形 B.m=1
C.△CEF的周长可以等于6 D.四边形CEDF的面积为2
12.如图,矩形false中,false,false,动点false从false点出发以false/秒向终点false运动,动点false同时从false点出发以false/秒按falsefalse的方向在边false,false,false上运动,设运动时间为false(秒),那么false的面积false随着时间false(秒)变化的函数图象大致为( )
B. C. D.
二、填空题
13.如图,在Rt△ACB中,∠ACB=90°,AC=BCfalse,D是AB上的一个动点,连接CD,将△BCD绕点C顺时针旋转90°得到△ACE,连接DE,则△ADE面积的最大值等于____________.
14.如图,抛物线false与函数false的图象在第一象限交点的横坐标为4,点false在抛物线上,点false在正比例函数的图象上,当false时,false的最大值为_______________.
15.如图,矩形false中AB=2,AD=5,动点P从点A出发,以1 cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则false面积最小值为_________.
16.如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始向B点以2cm/s的速度移动(不与点B重合);动点Q从点B开始向点C以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过_____秒四边形APQC的面积最小.
17.如图,在false中,false,false,false为false边上的高,动点false在false上,从点false出发,沿false方向运动,设false,false的面积为false,矩形false的面积为false,false,则false与false的关系式是________.
三、解答题
18.如图,正方形false的边长为false,false,false分别是false,false边上一动点,点false,false同时从点false出发,以每秒false的速度分别向点false,false运动,当点false与点false重合时,运动停止,设运动时间为false,运动过程中false的面积为false,求false关于false的函数表达式,并写出自变量false的取值范围.
19.如图,抛物线false经过false,false两点,点false是false轴左侧且位于false轴下方抛物线上一动点,设其横坐标为false.
(1)直接写出抛物线的解析式;
(2)将线段false绕点false顺时针旋转false得线段false(点false是点false的对应点),求点false的坐标,并判断点D是否在抛物线上;
(3)过点false作false轴交直线false于点false,试探究是否存在点false,使false是等腰三角形?若存在,求出点false的值;若不存在,说明理由.
20.如图,在矩形ABCD中,AB=4,AD=2.点P、Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P、Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x秒,△APQ的面积为S(平方单位).
(1)点P、Q从出发到相遇所用的时间是 秒.
(2)当2<x≤3时,求S与x之间的函数关系式 .
(3)当(2)的条件下,x为何值时,△APQ的面积为false.
21.在平面直角坐标系xOy中,抛物线y=﹣x2+2tx+2.
(1)求抛物线的对称轴(用含t的代数式表示);
(2)将点A(﹣1,3)向右平移5个单位长度,得到点B.
①若抛物线经过点B求t的值;
②若抛物线与线段AB恰有一个交点,结合函数图象直接写出t的取值范围.
22.如图,抛物线false与直线false相交于false,false两点,且抛物线经过点false
(1)求抛物线的解析式;
(2)点P是抛物线上的一个动点(不与点A.点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.当PE=2ED时,求P点坐标;
(3)点P是直线上方的抛物线上的一个动点,求false的面积最大时的P点坐标.
参考答案
1.B
解:有题意可知,false沿射线false运动的过程中,重叠面积y是先增加,然后不变,然后减小,最后为0
当false时,false,此时false,false无解;
当false时,false,令false,解得false;
当false时,false,false无解;
当false时,false,令false,解得false;
当false时,false,false无解;
综上所述,false或false
故答案选B.
2.C
解:设菱形的高为h,分三种情况:
①当P在BC边上时,
y=falseBP?h,
∵BP随x的增大而增大,h不变,
∴y随x的增大而增大,且为一次函数关系,
故选项A和D不正确;
②当P在边DC上时,
y=falseAB?h,
AB和h都不变,
∴在这个过程中,y不变,
故选项B不正确;
③当P在边AD上时,
y=falseAP?h,
∵PA随x的增大而减小,h不变,
∴y随x的增大而减小,且为一次函数,
故选:C;
3.C
解:∵点P(m,n)在直线y=?x+2上运动,
∴当m=1时,n=1,即P点在直线AO上,此时S=0,
设直线false与y轴交于点B,则B(0,2),连接AB,
∵点A的坐标为false,B(0,2),
∴false是等腰直角三角形,且false,
当m≤1时,S△APO=false×2×2-false×2×m×2=2?2m,
∴S与m是一次函数关系,
同理:当m>1时,S△APO=2m?2,故S与m是一次函数关系,
只有选项C符合题意.
故选:C.
4.C
解:false,
当点E在AB上运动时,即false时,
∵动点false同时从点A都以false的速度出发,
false.
false,
false为等边三角形,
false,
∴图象为开口向上的抛物线;
当点E在BC上运动时,即false时,此时false,
false.
∵四边形ABCD是菱形,
false,
false,
false为等边三角形,
false,
false,
false,
false,
false,
false,
∴图象为开口向下的抛物线,
综上所述,C选项符合题意,
故选:C.
5.B
解:①当点P在AB上运动时,则PB=3t,BQ=t,
则AP=3-3t,CQ=3-t,
S=S正方形ABCD-S△PBQ-S△ADP-S△CDQ=3×3-false[t?3t+(3-3t)×3+3(3-t)]=-falset2+6t,
该函数为开口向下的抛物线;
②当点P在AD上运动时,
则S=false×PD×AB=false×(3t-3)=falset-false;
③当点P在CD上运动时,
同理可得S=-false(t-2)(t-3)为开口向下的抛物线;
故选:B.
6.A
解:从图2看,false向右平移2个单位时,false整体到长方体中了,此时false与长方形DEFG重叠部分的面积为false的面积为false且false,
falsefalse的面积为false,
解得:false,
false.
false再向右平移3个单位时,点false重合,
故:false,
false长方形false的周长为false,
故选:A.
7.D
解:由题意得:设CF=2x,DE=x,
则BF=BC﹣FC=4﹣2x,AE=AD+DE=2+x,
则y=falseAE×BF=false×(2+x)(4﹣2x)=﹣x2+4(0≤x≤2),
故选:D.
8.A
解:过点P作PQ⊥x轴于Q,
根据题意,该抛物线的对称轴是直线x=false =1.设点Q的运动速度是每秒v个单位长度,
则∵当t=3和t=9时,n的值相等,
∴x=false[(9v?2)+(3v?2)] =1,
∴v=false .
①当t=6时,AQ=6×false =3,此时点P是抛物线顶点坐标,即n的值最大,故结论正确;
②当t=10时,AQ=10×false =5,此时点Q与点B不重合,即n≠0,故结论错误;
③当t=5时,AQ=false,此P时点的坐标是(false ,0);
当t=7时,AQ=false,此时点P的坐标是(false,0).
因为点(false,0)与点(false,0)关于对称轴直线x=1对称,所以n的值一定相等,故结论错误;
④t=4时,AQ=4×false=2,此时点Q与原点重合,则m=0,故结论正确.
综上所述,正确的结论是①④.
故选:A.
9.D
解:观察图象,可以发现函数图象由三个阶段构成,即△APQ的顶点Q所在边应有三种可能.
当Q的速度低于点P时,当点P到达A时,点Q还在DC上运动,之后,因A、P重合,△APQ的面积为零,画出图象只能有一个阶段构成,故A、B错误;
当Q的速度是点P速度的2倍,当点P到点A时,点Q到点B.之后,点A、P重合,△APQ的面积为0.
期间△APQ面积的变化可以看成两个阶段,与图象不符,故C错误.
故选:D.
10.D
解:设运动时间为false,
false点P到达点B所需时间为false,点Q到达点C所需时间为false,
false点P、Q同时停止运动,且false的取值范围为false,
由题意,false,
false,
false,
false,
则false与false之间的函数图象是抛物线在false的部分,且开口向下,
观察四个选项可知,只有选项D符合,
故选:D.
11.C
解:A.连接CD,
∵△ABC为等腰直角三角形,D是AB的中点,
∴CD=AD=BD,∠DCF=∠A=45°
而AE=CF,
∴△ADE≌△CDF(SAS),
∴DF=DE,∠CDF=∠ADE,
∴∠EDF=∠EDC+∠CDF=∠CDE+∠EDA=90°,CE=BF,
∴△DEF是等腰直角三角形,
故A正确;
B.设AC=BC=a,CE=BF=a﹣x,
S△CFE=false×CE×CF=falsex(a﹣x),
当x=falsea=false时,S△CFE有最大值=false×false×(2false﹣false)=1,
故m=1,此时a=4false,
故B正确;
C.△CEF的周长=EC+CF+EF=AC+EF=2false+EF,
而EF<CE+CF=2false,
即△CEF的周长=EC+CF+EF=AC+EF=2false+EF<4false<6,
故C错误;
D.四边形CEDF的面积=S△CDE+S△CDF=S△CDE+S△AED=S△ACD=falseS△ABC=false×false×2false×2false=2,
故D正确.
故选:C.
12.A
解:根据题意可知:AP=x,Q点运动路程为2x,
①当点Q在AD上运动时,
y=falseAP?AQ=falsex?2x=x2,图象为开口向上的二次函数;
②当点Q在DC上运动时,
y=falseAP?DA=falsex×3=false,是一次函数;
③当点Q在BC上运动时,
y=falseAP?BQ=falsex?(12?2x)=?x2+6x,为开口向下的二次函数,
结合图象可知A选项函数关系图正确,
故选:A.
13.false
解:如图,△BCD绕点C顺时针旋转90°得到△ACE,
∴△BDC≌△AEC,
∴∠B=∠CAE,
∵BC=AC=false,△ABC为等腰直角三角形,
∴∠B=∠CAE=∠BAC=45°,
∴∠DAE=∠BAC+∠CAE=90°,
在Rt△ABC中,由勾股定理AB=false,
设BD=AE=x,则AD=(2-x),
∴false,
∵false,函数开口向下,函数有最大值,
当x=1时,false.
故答案为:false.
14.false
解:把x=4代入false得y=2
把x=4,y=2代入false得false
解得a=false
∴false
当x=t时,false,当x=t+1时,false
∴当false时,false=false=false=false
∵false<0,
∴当t=2时,false的最大值为false
故答案为:false.
15.false
解:由题意得:AP=t,PD=5-t,
∴false,
∵四边形PCEF是正方形,
∴false,
∵false,
∴false,
∴false,
∴当t=4时,△DEF的面积最小,最小值为false.
故答案为:false.
16.3
解:设运动时间为t秒时(0≤t≤6),四边形APQC的面积为S,
∵PB=AB﹣2t=12﹣2t,BQ=4t,
∴S△BPQ=falsePB?BQ=false(12﹣2t)?4t=24t﹣4t2,
∴S=S△ABC﹣S△BPQ=falseAB?BC﹣(24t﹣4t2)=4t2﹣24t+144,
∵S=4t2﹣24t+144=4(t﹣3)2+108,
∴经过3秒四边形APQC的面积最小,
故答案为:3.
17.false
解:在false中,false,false,
∴false,
∵false为false边上的高,
∴AD=BD=DC=false
设false,
∴PD=false,
∵矩形false,由于DF在BC上,
∴PE∥DC,
∴∠AEP=∠C=∠DAC=45?,
∴PE=AP=x,
S1=false,
S2=false,
∴false,
false.
故答案为:false.
18.falsefalse
解:设运动时间为false,
false点false,false同时从点false出发,以每秒false的速度分别向点false,false运动,
false,false,false,false,
false的面积false正方形false的面积false的面积false的面积false的面积,
即:false
false
false false
19.(1)false;(2)false,点false不在抛物线上;(3)存在点false,使false是等腰三角形,false的值为false或false或false
解:(1)将false,false两点的坐标代入false得
false
解得false
∴抛物线的解析式为:
false
false作false轴于点false轴于点false,如下图,
则false
易证false
false
false
false
将x=-3代入false得
false,
∵false
false点false不在抛物线上.
false过点false作false轴交false于点false,
设直线false解析式为false,
则false,
解得false
false直线false解析式为false.
依题意false
false当false时,则false
false
解得false(舍去),false;
false当false时,则false,
解得false(舍去),false
false当false时,
false
false
false
false轴,
false点false的纵坐标为false
false,
解得false(舍去),false.
综上所述:存在点false,使false是等腰三角形,
false的值为false或false或false.
20.(1)4;(2)S=﹣x2+4x;(3)满足条件的x的值为2+false.
解:(1)(4×2+2×2)÷(2+1)=4(秒),
故答案为4.
(2)如图,当2<x≤3时,点P在线段BC上,点Q在线段CD上,
∴S=S矩形ABCD﹣S△ADQ﹣S△ABP﹣S△CPQ=4×2﹣false×2×(x﹣2)﹣false×4×(2x﹣4)﹣false×(6﹣x)×(6﹣2x)=﹣x2+4x.
故答案为:S=﹣x2+4x.
(3)当2<x≤3时,﹣x2+4x=false,
∴x=2±false,
∵2<x≤3,
∴x=2+false.
∴满足条件的x的值为2+false.
21.(1)直线x=t;(2)①t=false;②t≤﹣1或t=1或t>false时,抛物线与线段AB有一个公共点.
解:(1)∵抛物线y=﹣x2+2tx+2,
∴抛物线的对称轴为直线x=﹣false=t,
即抛物线的对称轴为直线x=t;
(2)点A(﹣1,3)向右平移5个长度单位,得到点B(4,3),
①∵抛物线经过点B,
∴3=﹣16+8t+2,
解得t=false;
②∵y=﹣x2+2tx+2=﹣(x﹣t)2+t2+2,
∴顶点的坐标为(t,t2+2),
由顶点的坐标可知,抛物线的顶点在抛物线y=x2+2上移动.
把y=3代入y=x2+2求得x=±1,
当抛物线过点A(﹣1,3)时,t=﹣1.
所以t≤﹣1或t=1或t>false时,抛物线与线段AB有一个公共点.
22.(1)y=?x2+4x+5(2)P点坐标为(2,9)或(6,?7);(3)P(false,false).
解:(1)∵点B(4,m)在直线y=x+1上,
∴m=4+1=5,
∴B(4,5),
把A、B、C三点坐标代入抛物线解析式可得
false,
解得
false,
∴抛物线解析式为y=?x2+4x+5;
(2)设P(x,?x2+4x+5),则E(x,x+1),D(x,0),
则PE=|?x2+4x+5?(x+1)|=|?x2+3x+4|,DE=|x+1|,
∵PE=2ED,
∴|?x2+3x+4|=2|x+1|,
当?x2+3x+4=2(x+1)时,解得x=?1或x=2,但当x=?1时,P与A重合不合题意,舍去,
∴P(2,9);
当?x2+3x+4=?2(x+1)时,解得x=?1或x=6,但当x=?1时,P与A重合不合题意,舍去,
∴P(6,?7);
综上可知P点坐标为(2,9)或(6,?7);
(3)∵点P是直线上方的抛物线上的一个动点,
设(x,?x2+4x+5),则E(x,x+1),D(x,0),
则PE=?x2+4x+5?(x+1)=?x2+3x+4,
∴false= Sfalse+ Sfalse=false=false
=false
∴当x=false,false的面积最大
把x=false代入y=?x2+4x+5,解得y=false
故P(false,false).
同课章节目录
