第二十七章 相似 章末复习 2021-2022学年人教版九年级数学下册(Word版 含答案)
文档属性
| 名称 | 第二十七章 相似 章末复习 2021-2022学年人教版九年级数学下册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 127.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-15 00:00:00 | ||
图片预览


文档简介
第二十七章 相似
一、填空题(每小题3分,共24分)
1.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20.则线段x的长是
2.边长为12cm的等边三角形按2:1的比例缩小后的三角形是边长为 的 三角形。
3.已知△ABC∽△DEF,AB=6,DE=8,则S△ABC :S△DEF =
4.已知三个数1,√2,2,请你再添一个数,写出一个比例式_
5.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得三角形与△ABC相似,满足这样条件的直线最多 条.
462724538106.电视节目主持人在主持节目时,站在舞台上的黄金分割点处最自然得体,若舞台AB长为20cm,试计算主持人应走到离A点至少 m处.(结果精确到0.1m)
7.一个4米高的电线杆的影长是6米,它临近的一个建筑物的影长是36米.则这个建筑的高度是 .
8.如图,若DE∥BC,FD∥AB,AD=AC=2:3,AB=9,BC=6,则四边形BEDF的周长为 .
二、选择题(每小题4分,共40分)
1.若果mn=ab,则下列比例式中不正确的是( )
A.am=nb B. an=mb C. ma=mb D. ma=bm
42945051981202.已知:如图2,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
A.ADAB=AEAC B. AEBC=ADBD C. DEBC=AEAB D. DEBC=ADDB
3.已知正五边形ABCDE与正五边形A'B'C'D'E'的面积比为1:2,则它们的相似比为( )
A1:2 B.2:1 C.1:√2 D.√2:1
42532302400304.如图,两个位似图形△ABO和△ABC,若OA:OA'=3:1,则正确的是( )
A. AB: A'B'=3: 1 B. AA': BB'=AB: AB'
C. OA: OB'=2:1 D.∠A=∠B
5.在比例尺是1:3800的南京交通游览图上,玄武湖隧道长约7cm,它的实际长度约为( )
A.0.266km
B.2.66km
C.26.6km
D.266000km
6.下列判断正确的是( )
A.不全等的三角形一定不是相似三角形
B.不相似的三角形一定不是全等三角形
C.相似三角形一定不是全等三角形
D.全等三角形不一定是相似三角形
46342302717807.如图,D、E是AB的三等分点,DF∥BG∥BC,图中三部分的面积分别为S1,S2,S3,则S1:S2:S3( )
A.1:2:3
B.1:2:4
C.1:3:5
D.2:3:4
8.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.无法判断谁的影子长
9.把△ABC的各边都扩大为原来的2倍,得到△A'B'C',下面结论不正确的是( )
A. △ABC∽△A'B'C'
B. △ABC和△A'B'C'的各边、各角对应相等
C. △ABC和△A'B'C'的相似比为1:2
D. △ABC和△A'B'C'的相似比为1:3
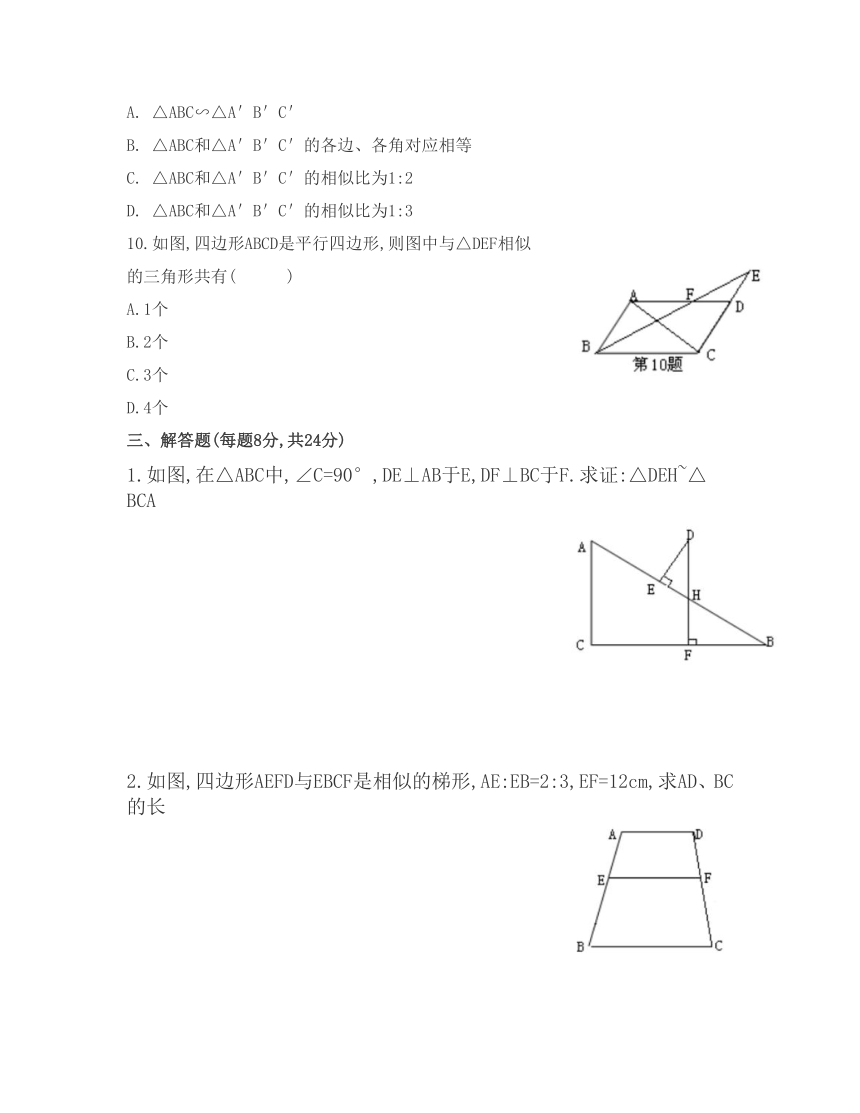
389255022352010.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个
B.2个
C.3个
D.4个
三、解答题(每题8分,共24分)
1.如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH~△BCA
397002012700
2.如图,四边形AEFD与EBCF是相似的梯形,AE:EB=2:3,EF=12cm,求AD、BC的长
397002041910
31775403384553.如图,平行四边形ABCD中,点E是DC中点,连AE并延长BC延长线交于点F,若S△CEF=10,求四边形ABCE的面积.
四.(12分)
38995358890已知如图,平行四边形ABCD中,AE:EB=1:2
(1)求AE:DC的值
(2)△AEF与△CDF相似吗?若相似,请说明理由,
并求出相似比.
(3)如果S△AEF=6cm2,求S△CDF
参考答案
一、填空题:
1.5 2.6cm,等边, 3.9:16, 4. 1:√2=2:2√2, 5.4 6.7.6m, 7.24m 8.14
二、选择题: CCCAA BCDDB
三、解答题
(1)证明:∵DE⊥AB,DF⊥BC
∴∠D+∠DHE=∠B+∠BHF=90°
而∠BHF=∠DHE
∴∠D=∠B
又∵∠HFB=∠C=90°
∴△DEH∽△BCA
(2)解:∵四边形AEFD∽四边形EBCF
∴ADEF=ABEB, EFBC=ABEB
∴AD=8,BC=18
(3)解:∵四边形ABCD为平行四边形
∴EC∥AB,DC=AB,由E为DC中点,
∴EC=12DC=12AB
∵EC∥AB,
∴∠ECF=∠ABF,
∠F=∠F
△ECF∽△ABF
∴EC:AB=1:2,S△ECF:S△ABF=1:4
S△ABF=40
△AED≌△FEC
∴S四边形ABCE=S△ABF=40
四、(1)∵ABCD为平行四边形
∴AB=CD
∴AE:DC=AE:EB=1:2
(2)相似
∵ABCD为平行四边形
∴DC∥AB
∴∠DCA=∠BAC
∠AFE=∠CFD
∴△AEF∽△CDF
(3)∵AE:DC =1:2
∴S△AEF:S△CDF=1:4
∴S△CDF=24cm2
一、填空题(每小题3分,共24分)
1.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20.则线段x的长是
2.边长为12cm的等边三角形按2:1的比例缩小后的三角形是边长为 的 三角形。
3.已知△ABC∽△DEF,AB=6,DE=8,则S△ABC :S△DEF =
4.已知三个数1,√2,2,请你再添一个数,写出一个比例式_
5.点P是△ABC中AB边上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得三角形与△ABC相似,满足这样条件的直线最多 条.
462724538106.电视节目主持人在主持节目时,站在舞台上的黄金分割点处最自然得体,若舞台AB长为20cm,试计算主持人应走到离A点至少 m处.(结果精确到0.1m)
7.一个4米高的电线杆的影长是6米,它临近的一个建筑物的影长是36米.则这个建筑的高度是 .
8.如图,若DE∥BC,FD∥AB,AD=AC=2:3,AB=9,BC=6,则四边形BEDF的周长为 .
二、选择题(每小题4分,共40分)
1.若果mn=ab,则下列比例式中不正确的是( )
A.am=nb B. an=mb C. ma=mb D. ma=bm
42945051981202.已知:如图2,在△ABC中,∠ADE=∠C,则下列等式成立的是( )
A.ADAB=AEAC B. AEBC=ADBD C. DEBC=AEAB D. DEBC=ADDB
3.已知正五边形ABCDE与正五边形A'B'C'D'E'的面积比为1:2,则它们的相似比为( )
A1:2 B.2:1 C.1:√2 D.√2:1
42532302400304.如图,两个位似图形△ABO和△ABC,若OA:OA'=3:1,则正确的是( )
A. AB: A'B'=3: 1 B. AA': BB'=AB: AB'
C. OA: OB'=2:1 D.∠A=∠B
5.在比例尺是1:3800的南京交通游览图上,玄武湖隧道长约7cm,它的实际长度约为( )
A.0.266km
B.2.66km
C.26.6km
D.266000km
6.下列判断正确的是( )
A.不全等的三角形一定不是相似三角形
B.不相似的三角形一定不是全等三角形
C.相似三角形一定不是全等三角形
D.全等三角形不一定是相似三角形
46342302717807.如图,D、E是AB的三等分点,DF∥BG∥BC,图中三部分的面积分别为S1,S2,S3,则S1:S2:S3( )
A.1:2:3
B.1:2:4
C.1:3:5
D.2:3:4
8.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.无法判断谁的影子长
9.把△ABC的各边都扩大为原来的2倍,得到△A'B'C',下面结论不正确的是( )
A. △ABC∽△A'B'C'
B. △ABC和△A'B'C'的各边、各角对应相等
C. △ABC和△A'B'C'的相似比为1:2
D. △ABC和△A'B'C'的相似比为1:3
389255022352010.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个
B.2个
C.3个
D.4个
三、解答题(每题8分,共24分)
1.如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH~△BCA
397002012700
2.如图,四边形AEFD与EBCF是相似的梯形,AE:EB=2:3,EF=12cm,求AD、BC的长
397002041910
31775403384553.如图,平行四边形ABCD中,点E是DC中点,连AE并延长BC延长线交于点F,若S△CEF=10,求四边形ABCE的面积.
四.(12分)
38995358890已知如图,平行四边形ABCD中,AE:EB=1:2
(1)求AE:DC的值
(2)△AEF与△CDF相似吗?若相似,请说明理由,
并求出相似比.
(3)如果S△AEF=6cm2,求S△CDF
参考答案
一、填空题:
1.5 2.6cm,等边, 3.9:16, 4. 1:√2=2:2√2, 5.4 6.7.6m, 7.24m 8.14
二、选择题: CCCAA BCDDB
三、解答题
(1)证明:∵DE⊥AB,DF⊥BC
∴∠D+∠DHE=∠B+∠BHF=90°
而∠BHF=∠DHE
∴∠D=∠B
又∵∠HFB=∠C=90°
∴△DEH∽△BCA
(2)解:∵四边形AEFD∽四边形EBCF
∴ADEF=ABEB, EFBC=ABEB
∴AD=8,BC=18
(3)解:∵四边形ABCD为平行四边形
∴EC∥AB,DC=AB,由E为DC中点,
∴EC=12DC=12AB
∵EC∥AB,
∴∠ECF=∠ABF,
∠F=∠F
△ECF∽△ABF
∴EC:AB=1:2,S△ECF:S△ABF=1:4
S△ABF=40
△AED≌△FEC
∴S四边形ABCE=S△ABF=40
四、(1)∵ABCD为平行四边形
∴AB=CD
∴AE:DC=AE:EB=1:2
(2)相似
∵ABCD为平行四边形
∴DC∥AB
∴∠DCA=∠BAC
∠AFE=∠CFD
∴△AEF∽△CDF
(3)∵AE:DC =1:2
∴S△AEF:S△CDF=1:4
∴S△CDF=24cm2
