2021年暑期学情跟踪:人教版数学八年级上册 13.1.1 轴对称(word版,含答案)
文档属性
| 名称 | 2021年暑期学情跟踪:人教版数学八年级上册 13.1.1 轴对称(word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 13:29:44 | ||
图片预览


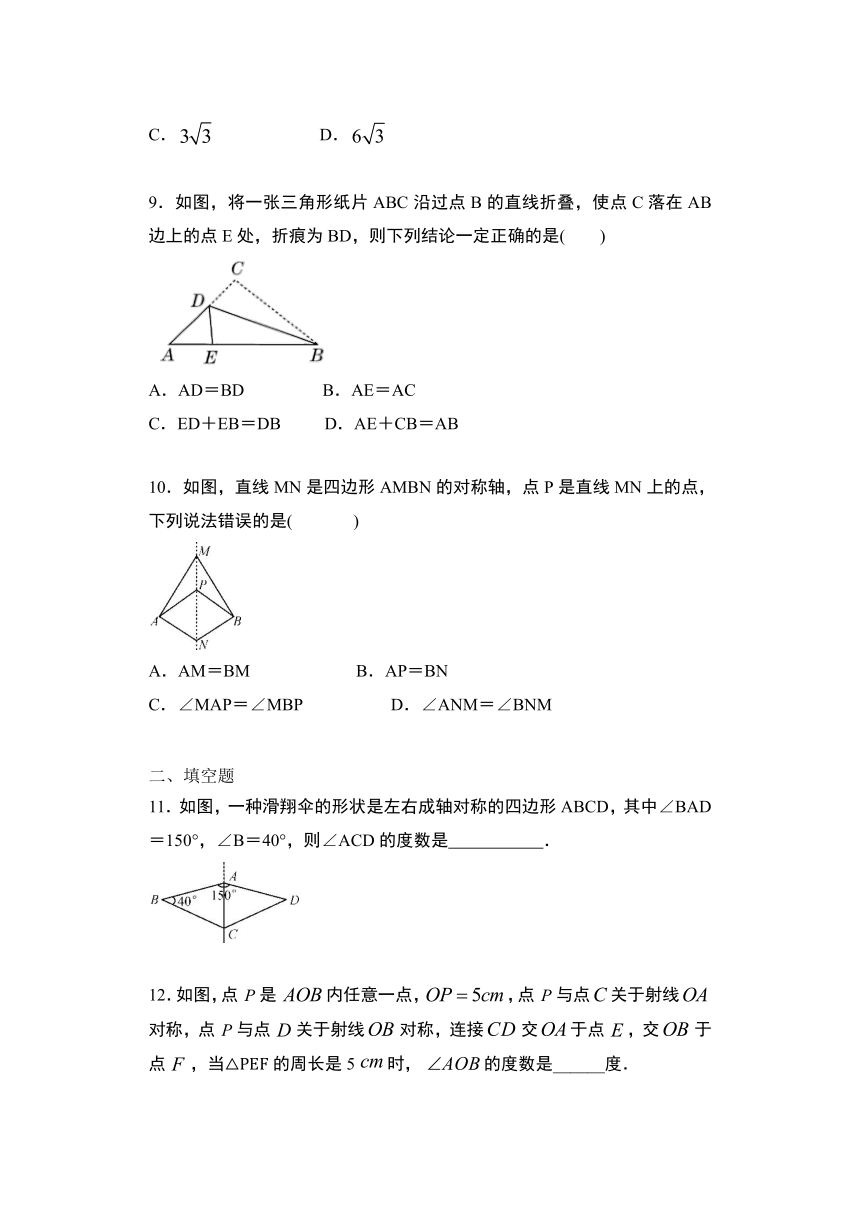
文档简介
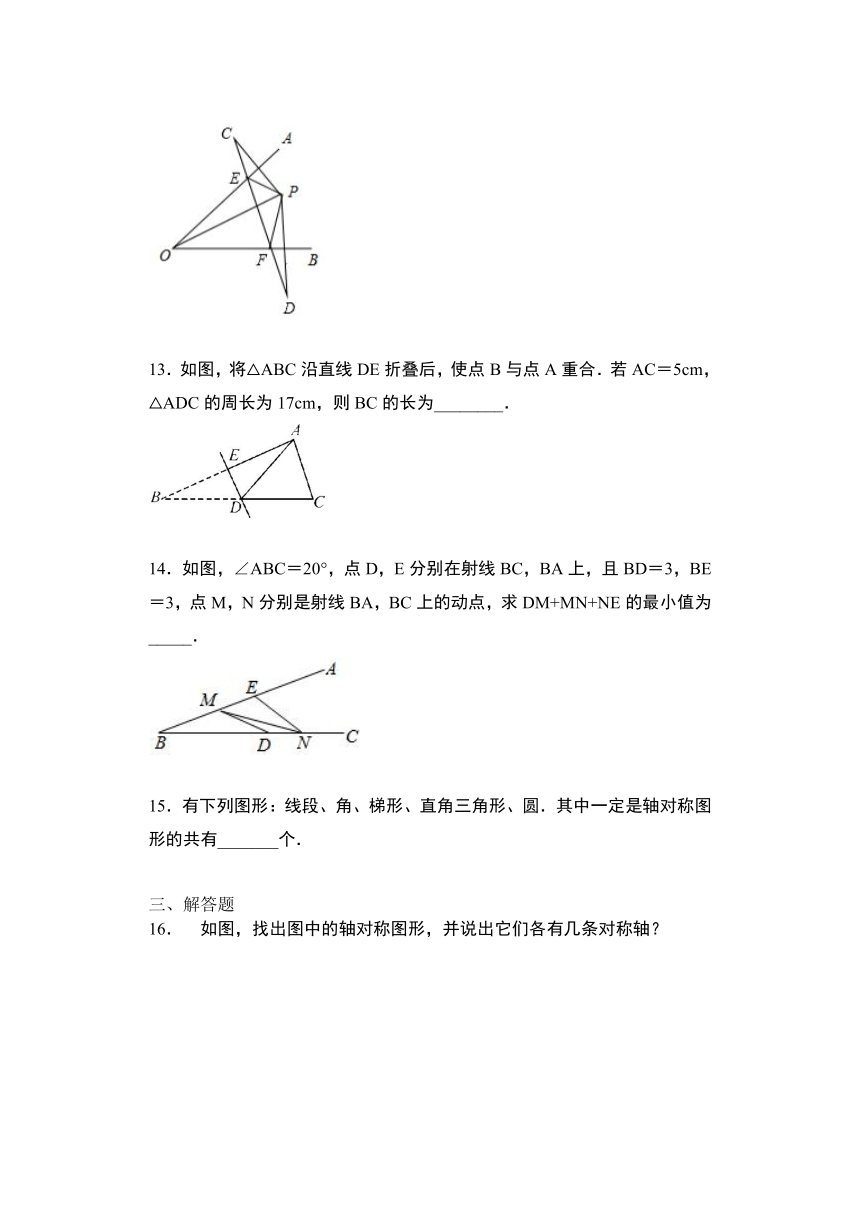
13.1.1
轴对称暑期学情跟踪练习
一、选择题
1.下列说法中,正确的是(
)
A.关于某条直线对称的两个三角形一定全等
B.两个全等三角形一定关于某条直线对称
C.面积相等的两个三角形一定关于某条直线对称
D.周长相等的两个三角形一定关于某条直线对称
2.有下列说法:①线段的对称轴有两条;②角是轴对称图形,它的平分线就是它的对称轴;③两点关于连接它们的线段的垂直平分线对称;④到直线l的距离相等的两个点关于直线l对称.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
3.如图的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
4.在一些汉字的美术字中,有的是轴对称图形,下面四个美术字中可以看作轴对称图形的是( )
5.下列图案中,不是轴对称图形的是(
)
A
B
C
D
6.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为(
)
A.27°
B.59°
C.69°
D.79°
7.把一张对边互相平行的纸条,折成如图所示,是折痕,若,则下列结论正确的有是( )
(1);(2);
(3);(4).
A.1个
B.2个
C.3个
D.4个
8.如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=6,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为(
)
A.3
B.6
C.
D.
9.如图,将一张三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD
B.AE=AC
C.ED+EB=DB
D.AE+CB=AB
10.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列说法错误的是(
)
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
二、填空题
11.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是
.
12.如图,点是内任意一点,,点与点关于射线对称,点与点关于射线对称,连接交于点,交于点,当△PEF的周长是5时,的度数是______度.
13.如图,将△ABC沿直线DE折叠后,使点B与点A重合.若AC=5cm,△ADC的周长为17cm,则BC的长为________.
14.如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
15.有下列图形:线段、角、梯形、直角三角形、圆.其中一定是轴对称图形的共有_______个.
三、解答题
16.
如图,找出图中的轴对称图形,并说出它们各有几条对称轴?
17.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
18.定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是
,推断的数学依据是
.
(2)如图②,在△ABC中,∠B=45°,AB=3,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
19.如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β
|=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
20.
如图所示,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.
若MN=20
cm,求△PEF的周长;
21.
如图,O为△ABC内部一点,OB=3,P、R为O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于6,并说明理由;
(2)结合(1),请判断当∠ABC不是你指出的角度时,PR的长度是小于6还是大于6,并说明理由.
答案
一、选择题
1.
A
2.
C
3.
C
4.
D
5.
B
6.
D
7.
C
8.
B
9.
D
10.
B
二、填空题
11.
65°
12.
30
13.
12cm
14.
3
15.
3
三、解答题
16.
解:⑴是轴对称图形,有3条对称轴;
⑵是轴对称图形,有5条对称轴;
⑶是轴对称图形,有4条对称轴;
⑷是轴对称图形,有1条对称轴;
⑸是轴对称图形,有2条对称轴;
⑹不是轴对称图形.
17.
解:∵两个四边形关于直线l对称,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
a=5
cm,b=4
cm.
∴∠G=360°-∠H-∠E-∠F=55°.
18.
(1)等腰三角形;线段的垂直平分线上的点到两端的距离相等;(2)1;(3).
19.
(1)35°或125°;(2)45°或75°;(3)10°或130°.
20.
解:如图,设MP与OA相交于点R,PN与OB相交于点T.
∵点M,N分别是点P关于直线OA,OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴MR=PR,∠MRE=∠PRE=90°,
PT=NT,∠PTF=∠NTF=90°.
又∵RE=RE,∴△MRE≌△PRE(SAS),∴ME=PE.
又∵FT=FT,∴△PTF≌△NTF(SAS),
∴NF=PF,
∴PE+EF+PF=ME+EF+NF=MN=20
cm,
即△PEF的周长是20
cm.
21.
解:(1)当∠ABC=90°时,PR=6.
证明:如图,连接PB、RB,
∵P、R为O分别以直线AB、直线BC为对称轴的对称点,∴PB=OB=3,RB=OB=3,∵∠ABC=90°,
∴∠ABP+∠CBR=∠ABO+∠CBO=∠ABC=90°,
∴P、B、R三点共线,∴PR=2×3=6.
(2)PR的长度小于6.
理由:当∠ABC≠90°时,P、B、R三点不在同一直线上,
∴PB+BR>PR,∵PB+BR=2OB=2×3=6,∴PR<6.
试卷第8页,总8页
轴对称暑期学情跟踪练习
一、选择题
1.下列说法中,正确的是(
)
A.关于某条直线对称的两个三角形一定全等
B.两个全等三角形一定关于某条直线对称
C.面积相等的两个三角形一定关于某条直线对称
D.周长相等的两个三角形一定关于某条直线对称
2.有下列说法:①线段的对称轴有两条;②角是轴对称图形,它的平分线就是它的对称轴;③两点关于连接它们的线段的垂直平分线对称;④到直线l的距离相等的两个点关于直线l对称.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
3.如图的五角星是轴对称图形,它的对称轴共有( )
A.1条
B.3条
C.5条
D.无数条
4.在一些汉字的美术字中,有的是轴对称图形,下面四个美术字中可以看作轴对称图形的是( )
5.下列图案中,不是轴对称图形的是(
)
A
B
C
D
6.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为(
)
A.27°
B.59°
C.69°
D.79°
7.把一张对边互相平行的纸条,折成如图所示,是折痕,若,则下列结论正确的有是( )
(1);(2);
(3);(4).
A.1个
B.2个
C.3个
D.4个
8.如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=6,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为(
)
A.3
B.6
C.
D.
9.如图,将一张三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD
B.AE=AC
C.ED+EB=DB
D.AE+CB=AB
10.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列说法错误的是(
)
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
二、填空题
11.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是
.
12.如图,点是内任意一点,,点与点关于射线对称,点与点关于射线对称,连接交于点,交于点,当△PEF的周长是5时,的度数是______度.
13.如图,将△ABC沿直线DE折叠后,使点B与点A重合.若AC=5cm,△ADC的周长为17cm,则BC的长为________.
14.如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
15.有下列图形:线段、角、梯形、直角三角形、圆.其中一定是轴对称图形的共有_______个.
三、解答题
16.
如图,找出图中的轴对称图形,并说出它们各有几条对称轴?
17.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
18.定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是
,推断的数学依据是
.
(2)如图②,在△ABC中,∠B=45°,AB=3,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
19.如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β
|=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
20.
如图所示,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.
若MN=20
cm,求△PEF的周长;
21.
如图,O为△ABC内部一点,OB=3,P、R为O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于6,并说明理由;
(2)结合(1),请判断当∠ABC不是你指出的角度时,PR的长度是小于6还是大于6,并说明理由.
答案
一、选择题
1.
A
2.
C
3.
C
4.
D
5.
B
6.
D
7.
C
8.
B
9.
D
10.
B
二、填空题
11.
65°
12.
30
13.
12cm
14.
3
15.
3
三、解答题
16.
解:⑴是轴对称图形,有3条对称轴;
⑵是轴对称图形,有5条对称轴;
⑶是轴对称图形,有4条对称轴;
⑷是轴对称图形,有1条对称轴;
⑸是轴对称图形,有2条对称轴;
⑹不是轴对称图形.
17.
解:∵两个四边形关于直线l对称,
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,
a=5
cm,b=4
cm.
∴∠G=360°-∠H-∠E-∠F=55°.
18.
(1)等腰三角形;线段的垂直平分线上的点到两端的距离相等;(2)1;(3).
19.
(1)35°或125°;(2)45°或75°;(3)10°或130°.
20.
解:如图,设MP与OA相交于点R,PN与OB相交于点T.
∵点M,N分别是点P关于直线OA,OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴MR=PR,∠MRE=∠PRE=90°,
PT=NT,∠PTF=∠NTF=90°.
又∵RE=RE,∴△MRE≌△PRE(SAS),∴ME=PE.
又∵FT=FT,∴△PTF≌△NTF(SAS),
∴NF=PF,
∴PE+EF+PF=ME+EF+NF=MN=20
cm,
即△PEF的周长是20
cm.
21.
解:(1)当∠ABC=90°时,PR=6.
证明:如图,连接PB、RB,
∵P、R为O分别以直线AB、直线BC为对称轴的对称点,∴PB=OB=3,RB=OB=3,∵∠ABC=90°,
∴∠ABP+∠CBR=∠ABO+∠CBO=∠ABC=90°,
∴P、B、R三点共线,∴PR=2×3=6.
(2)PR的长度小于6.
理由:当∠ABC≠90°时,P、B、R三点不在同一直线上,
∴PB+BR>PR,∵PB+BR=2OB=2×3=6,∴PR<6.
试卷第8页,总8页
