用频率估计概率
图片预览








文档简介
(共20张PPT)
25.3 用频率估计概率(1)
必然事件:一定能发生事件
不可能事件:一定不能发生事件
可能性的大小:
0 (50%) 1(100%)
不可能发生
可能发生
必然发生
随机事件:(不确定事件)
用列举法求概率的条件是什么
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢
问题
1.掷一次骰子,向上的一面数字是6的概率是____.
2.某射击运动员射击一次,命中靶心的概率是____.
命中靶心与未命中靶心发生可能性不相等
试验的结果不是有限个的
1
6
各种结果发生的可能性相等
试验的结果是有限个的
等可能事件
25.3 用频率估计概率(1)
在实验中,每个对象出现的次数称为频数,
事件发生的可能性,也称为事件发生的概率.
频率=
A可能发生的情况
可能发生的总情况
频数:
频率:
所考察对象出现的次数与实验的总次数的比叫做频率
概率:
做抛硬币的实验:当抛一枚硬币时会出现几种结果?—— 其中正面朝上的概率是多少?——无论抛多少次,正面朝上的概率会不会改变?——
若抛10次,其中4次正面朝上,则正面朝上的频率是多少?——如果有5次正面向上呢?——频率是否会改变?
这就是说同次试验的频率和概率是否相同?
________________
2种
0.5
不变
0.4
0.5
会改变
有时相同,有时不相同
全班分成九组,每组同学掷一枚硬币50次,
记录好“正面向上”的次数,
计算出“正面向上”的频率.
50
抛掷次数n
“正面向上”的频数m
“正面向上”的频率m/n
投掷次数
正面向上的频率m/n
0
50
100
150
200
250
300
350
400
450
500
0.5
1
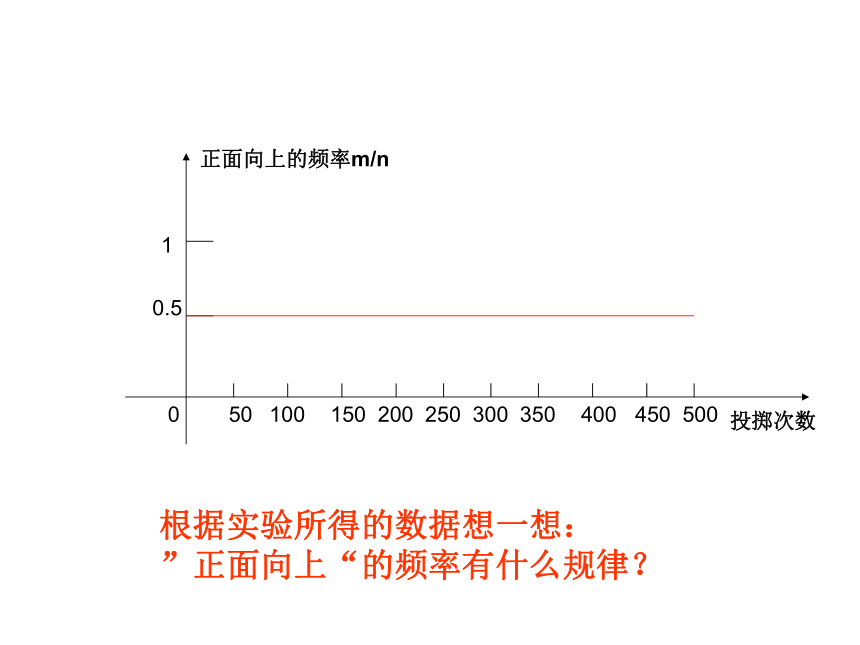
根据实验所得的数据想一想:
”正面向上“的频率有什么规律?
试验者 抛掷次数n “正面向上”
次数m “正面向上”频率m/n
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10 000 4979 0.4979
皮尔逊 12 000 6019 0.5016
皮尔逊 24 000 12012 0.5005
随着抛掷次数的增加,“正面向上”
的频率的变化趋势有何规律
事件A的概率的定义:
一般地,在大量重复试验中,如果
事件A发生的频率 会稳定在某个常
数p附近,那么这个常数p叫做事件A的概率。
记为P(A)=p 或 P(A)=
某批乒乓球产品质量检查结果表:
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数
抽取球数
在这批乒乓球产品中优等品的概率是多少?
(精确到0.01)
0.95
概率是通过大量重复试验中频率的稳定性得到的一个0-1的常数,它反映了事件发生的可能性的大小.
“抛掷一枚硬币50次,则“正面向上”的
次数必为25次.”这句话对吗
概率是针对大量试验而言的,大量试验反
映的规律并非在每次试验中一定存在.
例:对一批衬衫进行抽检,结果如下表所示:
抽取件数n 50 100 150 200 500 800 1000
优等品件数m 42 88 141 176 445 724 901
优等品频率m/n 0.84 0.88 0.94 0.88 0.89 0.905 0.901
求抽取一件衬衫是优等品的概率约是多少?
解:从表中可以看出,当抽取件数n越大,“抽取一件衬衫的是优等品”事件发生的频率就越接近常数0.90,所以抽取一件衬衫是优等品的概率约为0.90。
某足球运动员在同一条件下进行射门,结果如下表所示:
射门次数n 20 50 100 200 500 800
踢进球门次数m 13 35 58 104 255 404
踢进球门频率m/n
计算表中踢进球门的各个频率;
这个运动员射门一次,
射进球门的概率约是多少?
估计这个运动员射门1600次,
射进球门的次数约是多少?
小结
随机事件的概率的定义
在大量重复进行同一试验时, 事件 发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率.
由定义可知:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此 .
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率;
1.盒子中有白色乒乓球8个和黄色乒乓球若干个,为求得盒中黄色乒乓球的个数,某同学进行了如下实验:每次摸出一个乒乓球记下它的颜色,如此重复360次,摸出白色乒乓球90次,则黄色乒乓球的个数估计为( )
A.90个 B.24个 C.70个 D.32个
2.从生产的一批螺钉中抽取1000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品概率约为( ).
A. B.
C. D.
3.某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来有( ).
A.10粒 B.160粒
C.450粒 D.500粒
25.3 用频率估计概率(1)
必然事件:一定能发生事件
不可能事件:一定不能发生事件
可能性的大小:
0 (50%) 1(100%)
不可能发生
可能发生
必然发生
随机事件:(不确定事件)
用列举法求概率的条件是什么
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢
问题
1.掷一次骰子,向上的一面数字是6的概率是____.
2.某射击运动员射击一次,命中靶心的概率是____.
命中靶心与未命中靶心发生可能性不相等
试验的结果不是有限个的
1
6
各种结果发生的可能性相等
试验的结果是有限个的
等可能事件
25.3 用频率估计概率(1)
在实验中,每个对象出现的次数称为频数,
事件发生的可能性,也称为事件发生的概率.
频率=
A可能发生的情况
可能发生的总情况
频数:
频率:
所考察对象出现的次数与实验的总次数的比叫做频率
概率:
做抛硬币的实验:当抛一枚硬币时会出现几种结果?—— 其中正面朝上的概率是多少?——无论抛多少次,正面朝上的概率会不会改变?——
若抛10次,其中4次正面朝上,则正面朝上的频率是多少?——如果有5次正面向上呢?——频率是否会改变?
这就是说同次试验的频率和概率是否相同?
________________
2种
0.5
不变
0.4
0.5
会改变
有时相同,有时不相同
全班分成九组,每组同学掷一枚硬币50次,
记录好“正面向上”的次数,
计算出“正面向上”的频率.
50
抛掷次数n
“正面向上”的频数m
“正面向上”的频率m/n
投掷次数
正面向上的频率m/n
0
50
100
150
200
250
300
350
400
450
500
0.5
1
根据实验所得的数据想一想:
”正面向上“的频率有什么规律?
试验者 抛掷次数n “正面向上”
次数m “正面向上”频率m/n
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10 000 4979 0.4979
皮尔逊 12 000 6019 0.5016
皮尔逊 24 000 12012 0.5005
随着抛掷次数的增加,“正面向上”
的频率的变化趋势有何规律
事件A的概率的定义:
一般地,在大量重复试验中,如果
事件A发生的频率 会稳定在某个常
数p附近,那么这个常数p叫做事件A的概率。
记为P(A)=p 或 P(A)=
某批乒乓球产品质量检查结果表:
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数
抽取球数
在这批乒乓球产品中优等品的概率是多少?
(精确到0.01)
0.95
概率是通过大量重复试验中频率的稳定性得到的一个0-1的常数,它反映了事件发生的可能性的大小.
“抛掷一枚硬币50次,则“正面向上”的
次数必为25次.”这句话对吗
概率是针对大量试验而言的,大量试验反
映的规律并非在每次试验中一定存在.
例:对一批衬衫进行抽检,结果如下表所示:
抽取件数n 50 100 150 200 500 800 1000
优等品件数m 42 88 141 176 445 724 901
优等品频率m/n 0.84 0.88 0.94 0.88 0.89 0.905 0.901
求抽取一件衬衫是优等品的概率约是多少?
解:从表中可以看出,当抽取件数n越大,“抽取一件衬衫的是优等品”事件发生的频率就越接近常数0.90,所以抽取一件衬衫是优等品的概率约为0.90。
某足球运动员在同一条件下进行射门,结果如下表所示:
射门次数n 20 50 100 200 500 800
踢进球门次数m 13 35 58 104 255 404
踢进球门频率m/n
计算表中踢进球门的各个频率;
这个运动员射门一次,
射进球门的概率约是多少?
估计这个运动员射门1600次,
射进球门的次数约是多少?
小结
随机事件的概率的定义
在大量重复进行同一试验时, 事件 发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率.
由定义可知:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此 .
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率;
1.盒子中有白色乒乓球8个和黄色乒乓球若干个,为求得盒中黄色乒乓球的个数,某同学进行了如下实验:每次摸出一个乒乓球记下它的颜色,如此重复360次,摸出白色乒乓球90次,则黄色乒乓球的个数估计为( )
A.90个 B.24个 C.70个 D.32个
2.从生产的一批螺钉中抽取1000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品概率约为( ).
A. B.
C. D.
3.某人把50粒黄豆染色后与一袋黄豆充分混匀,接着抓出100黄豆,数出其中有10粒黄豆被染色,则这袋黄豆原来有( ).
A.10粒 B.160粒
C.450粒 D.500粒
同课章节目录
