2.3.2气体的等圧変化和等容变化 课件—2020-2021学年高二下学期物理人教版(19张PPT)选择性必修第三册
文档属性
| 名称 | 2.3.2气体的等圧変化和等容变化 课件—2020-2021学年高二下学期物理人教版(19张PPT)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-13 06:29:39 | ||
图片预览



文档简介
2.3.2 气体的等压变化和等容变化
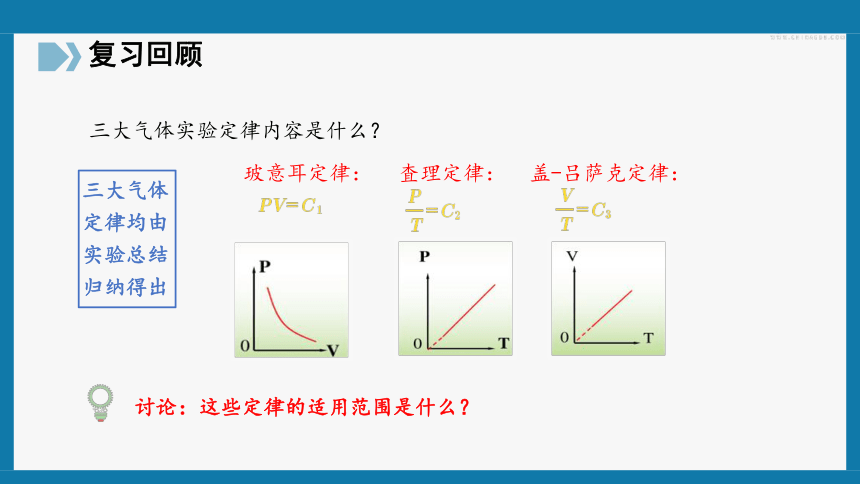
三大气体实验定律内容是什么?
玻意耳定律:
査理定律:
盖-吕萨克定律:
三大气体定律均由实验总结归纳得出
讨论:这些定律的适用范围是什么?
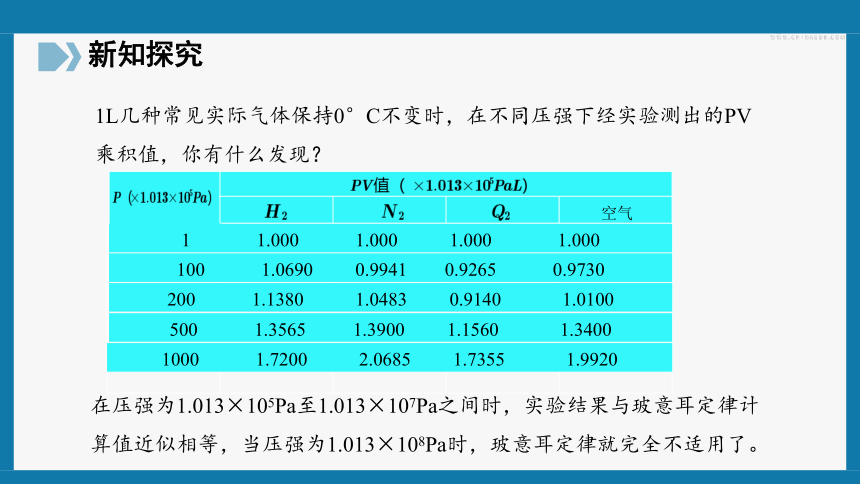
在压强为1.013×105Pa至1.013×107Pa之间时,实验结果与玻意耳定律计算值近似相等,当压强为1.013×108Pa时,玻意耳定律就完全不适用了。
空气
1? ? ? ? ? ? ??1.000? ? ? ? ? ? 1.000? ? ? ? ?? 1.000? ? ? ? ? ? ??1.000
100? ? ? ? ? ?1.0690? ? ? ? ?0.9941? ? ? ? 0.9265? ? ? ? ? ? 0.9730
200?? ? ? ? ? ?1.1380? ? ? ? ? ?1.0483? ? ? ? ?0.9140? ? ? ? ? ? ?1.0100
500?? ? ? ? ? ?1.3565? ?? ? ? ?1.3900? ? ? ? ?1.1560? ? ? ? ? ? ?1.3400
1000? ? ? ? ? ? 1.7200? ? ? ? ? ?2.0685? ? ? ? ?1.7355? ? ? ? ? ? ?1.9920
1L几种常见实际气体保持0°C不变时,在不同压强下经实验测出的PV乘积值,你有什么发现?
一、理想气体
设想有这样一种气体,它在任何温度和任何压强下都能严格地遵从气体实验定律,我们把这样的气体叫做“理想气体”。
理想气体的特点:
①严格遵守气体实验定律;
②理想气体分子本身的大小与分子间的距离相比可以忽略不计,分子可视为质点;
③理想气体分子除碰撞外,无相互作用的引力和斥力。
注意:
理想气体是为了研究问题方便而提出的一种理想模型,是实际气体的一种近似,实际上并不存在,就像力学中的质点、电学中的点电荷模型一样。
从宏观上讲,实际气体在压强不太大(不超过大气压的几倍) 、温度不太低(不低于零下几十摄氏度)的条件下,可视为理想气体。
如氢、氧气、氢气不易液化的气体。
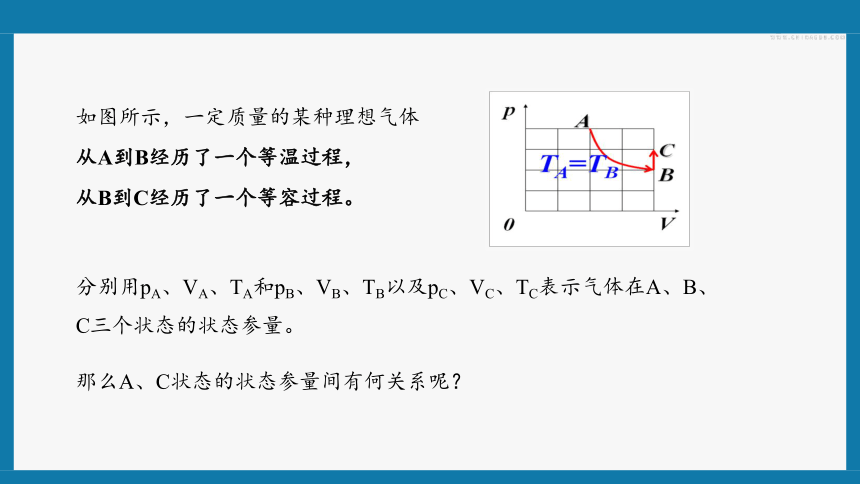
如图所示,一定质量的某种理想气体
从A到B经历了一个等温过程,
从B到C经历了一个等容过程。
那么A、C状态的状态参量间有何关系呢?
分别用pA、VA、TA和pB、VB、TB以及pC、VC、TC表示气体在A、B、C三个状态的状态参量。
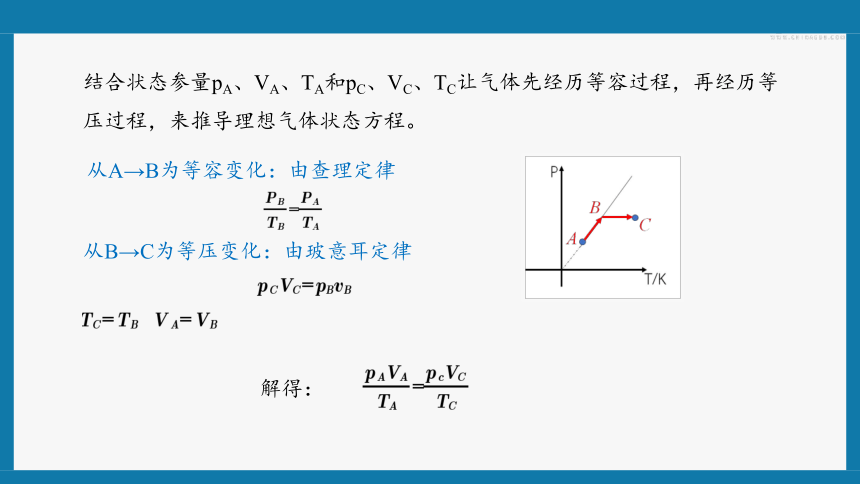
结合状态参量pA、VA、TA和pC、VC、TC让气体先经历等容过程,再经历等压过程,来推导理想气体状态方程。
从A→B为等容变化:由查理定律
从B→C为等压变化:由玻意耳定律
解得:
由于A、C两态是任意的,因此,上式可推广到任意的两态之间,即对一定质量的气体,无论其状态如何变化,都满足
理想气体状态方程:一定质量的某种理想气体在从一个状态变化到另一个状态时,尽管p、V、T都可能改变,但是压强跟体积的乘积与热力学温度的比值保持不变。
二、气体实验定律的微观解释
玻意耳定律的微观解释:
等温变化
T不变
分子平均动能不变,平均每个分子对器壁的撞击力不变
V减小
分子密集程度增大
单位时间内撞击容器单位面积的分子数增多
气体压强增大
查理定律(等容变化)的微观解释:
分子的密集程度不变
温度升高
分子的平均动能增加
压强越大
一定质量的气体,体积不变
盖-吕萨克定律(等压变化)的微观解释:
分子的平均动能增大
压强有增大的趋势
体积增大
压强有减小的趋势
一定质量的气体,温度升高
保持压强不变
气体的等压变化和等容变化
理想气体
对气体实验定律的微观解释
1.容器内一定质量的理想气体,在温度保持不变的条件下,若气体体积减小,则( )
A.气体分子热运动的平均动能增大
B.气体分子对器壁撞击的密集程度变大
C.气体中每个分子对器壁的撞击的作用力都变大
D.气体需要从外界吸收热量
B
2.如图,一定质量的气体从状态A沿直线变化到状态B的过程中,其温度( )
A.保持不变 B.逐渐升高
C.逐渐降低 D.先升高后降低
C
3.关于理想气体,下列说法正确的是( )
A.理想气体也不能严格地遵守气体实验定律
B.实际气体在温度不太高、压强不太小的情况下,可看成理想气体
C.实际气体在温度不太低、压强不太大的情况下,可看成理想气体
D.所有的实际气体在任何情况下,都可以看成理想气体
C
4.一个足球的容积是2.5L.用打气筒给这个足球打气,每打一次都把体积为125mL压强与大气压相同的气体打进球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,则打了20次时,足球内部空气的压强P与大气压P0的关系正确的是( )
A.P=2P0 B.P>2P0 C.P<2P0 D.不确定
A
5.下面有关理想气体的说法正确的是( )
A.分子本身的大小不可忽略
B.一定质量的理想气体,内能只与温度有关
C.分子与分子之间的相互作用力表现为斥力
D.所有气体都可视为理想气体
B
再见
三大气体实验定律内容是什么?
玻意耳定律:
査理定律:
盖-吕萨克定律:
三大气体定律均由实验总结归纳得出
讨论:这些定律的适用范围是什么?
在压强为1.013×105Pa至1.013×107Pa之间时,实验结果与玻意耳定律计算值近似相等,当压强为1.013×108Pa时,玻意耳定律就完全不适用了。
空气
1? ? ? ? ? ? ??1.000? ? ? ? ? ? 1.000? ? ? ? ?? 1.000? ? ? ? ? ? ??1.000
100? ? ? ? ? ?1.0690? ? ? ? ?0.9941? ? ? ? 0.9265? ? ? ? ? ? 0.9730
200?? ? ? ? ? ?1.1380? ? ? ? ? ?1.0483? ? ? ? ?0.9140? ? ? ? ? ? ?1.0100
500?? ? ? ? ? ?1.3565? ?? ? ? ?1.3900? ? ? ? ?1.1560? ? ? ? ? ? ?1.3400
1000? ? ? ? ? ? 1.7200? ? ? ? ? ?2.0685? ? ? ? ?1.7355? ? ? ? ? ? ?1.9920
1L几种常见实际气体保持0°C不变时,在不同压强下经实验测出的PV乘积值,你有什么发现?
一、理想气体
设想有这样一种气体,它在任何温度和任何压强下都能严格地遵从气体实验定律,我们把这样的气体叫做“理想气体”。
理想气体的特点:
①严格遵守气体实验定律;
②理想气体分子本身的大小与分子间的距离相比可以忽略不计,分子可视为质点;
③理想气体分子除碰撞外,无相互作用的引力和斥力。
注意:
理想气体是为了研究问题方便而提出的一种理想模型,是实际气体的一种近似,实际上并不存在,就像力学中的质点、电学中的点电荷模型一样。
从宏观上讲,实际气体在压强不太大(不超过大气压的几倍) 、温度不太低(不低于零下几十摄氏度)的条件下,可视为理想气体。
如氢、氧气、氢气不易液化的气体。
如图所示,一定质量的某种理想气体
从A到B经历了一个等温过程,
从B到C经历了一个等容过程。
那么A、C状态的状态参量间有何关系呢?
分别用pA、VA、TA和pB、VB、TB以及pC、VC、TC表示气体在A、B、C三个状态的状态参量。
结合状态参量pA、VA、TA和pC、VC、TC让气体先经历等容过程,再经历等压过程,来推导理想气体状态方程。
从A→B为等容变化:由查理定律
从B→C为等压变化:由玻意耳定律
解得:
由于A、C两态是任意的,因此,上式可推广到任意的两态之间,即对一定质量的气体,无论其状态如何变化,都满足
理想气体状态方程:一定质量的某种理想气体在从一个状态变化到另一个状态时,尽管p、V、T都可能改变,但是压强跟体积的乘积与热力学温度的比值保持不变。
二、气体实验定律的微观解释
玻意耳定律的微观解释:
等温变化
T不变
分子平均动能不变,平均每个分子对器壁的撞击力不变
V减小
分子密集程度增大
单位时间内撞击容器单位面积的分子数增多
气体压强增大
查理定律(等容变化)的微观解释:
分子的密集程度不变
温度升高
分子的平均动能增加
压强越大
一定质量的气体,体积不变
盖-吕萨克定律(等压变化)的微观解释:
分子的平均动能增大
压强有增大的趋势
体积增大
压强有减小的趋势
一定质量的气体,温度升高
保持压强不变
气体的等压变化和等容变化
理想气体
对气体实验定律的微观解释
1.容器内一定质量的理想气体,在温度保持不变的条件下,若气体体积减小,则( )
A.气体分子热运动的平均动能增大
B.气体分子对器壁撞击的密集程度变大
C.气体中每个分子对器壁的撞击的作用力都变大
D.气体需要从外界吸收热量
B
2.如图,一定质量的气体从状态A沿直线变化到状态B的过程中,其温度( )
A.保持不变 B.逐渐升高
C.逐渐降低 D.先升高后降低
C
3.关于理想气体,下列说法正确的是( )
A.理想气体也不能严格地遵守气体实验定律
B.实际气体在温度不太高、压强不太小的情况下,可看成理想气体
C.实际气体在温度不太低、压强不太大的情况下,可看成理想气体
D.所有的实际气体在任何情况下,都可以看成理想气体
C
4.一个足球的容积是2.5L.用打气筒给这个足球打气,每打一次都把体积为125mL压强与大气压相同的气体打进球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,则打了20次时,足球内部空气的压强P与大气压P0的关系正确的是( )
A.P=2P0 B.P>2P0 C.P<2P0 D.不确定
A
5.下面有关理想气体的说法正确的是( )
A.分子本身的大小不可忽略
B.一定质量的理想气体,内能只与温度有关
C.分子与分子之间的相互作用力表现为斥力
D.所有气体都可视为理想气体
B
再见
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
